递推思想
作为一个学渣的我,当再次看到阔别已久的数学公式,差点泪流满面啊,想当初,这些东西可没少折磨我啊,但是没厌恶,只有亲切!
一: 概念
通过已知条件,利用特定关系逐步递推,最终得到结果为止,核心就是不断的利用现有信息推导出新的东西。
二:分类
当然递推中有两种,“顺推”和“逆推“
顺推:从条件推出结果。
逆推:从结果推出条件。
呵呵,是不是觉的有一种policeman破案的感觉。
三: 举例
<1> 顺推的例子
上过大学的应该都知道著名的“斐波那契”数列吧,说的是繁殖兔子的问题,题目我就大概说一下。
如果1对兔子每月能生1对小兔子,而每对小兔在它出生后的第3个月就可以生1对小兔子,如果从1对初生的小兔子开始,1年后能
繁殖多少兔子?
思路:其实这个问题我们可以将兔子划分为“1月大的兔子“,”2月大的兔子“,”3月大的兔子“。
① 初始时: 一对1月大小兔子,总数为1对。
② 第一个月: 1月大的小兔子变成2月大的兔子,总数还是1对。
③ 第二个月: 2月大的小兔子变成3月大的兔子,繁殖了一对小兔子,总数为2对。
④ 第三个月: 3月大的兔子tmd有生了一对小兔子,上个月1月大的小兔子变成了2月大的兔子,总数为3对。
...... ......
F0=1
F1=1
F2=F0+F1
F3=F1+F2
......
Fn=Fn-2+Fn-1
大家看看,是不是体现了”递推“的核心思想,代码也很简单。
int month = 12;
int[] fab = new int[month];
fab[0] = 1;
fab[1] = 1;
//从已知条件出发推出结果
for (int i = 2; i < month; i++)
{
fab[i] = fab[i - 1] + fab[i - 2];
}
for (int i = 0; i < month; i++)
{
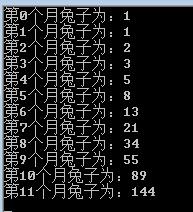
Console.WriteLine("第{0}个月兔子为:{1}", i, fab[i]);
}
<2> 逆推的例子
这个一个关于存钱的问题,一个富二代给他儿子的四年大学生活存一笔钱,富三代每月只能取3k作为下个月的生活费,采用的是整存零取的方式,
年利率在1.71%,请问富二代需要一次性存入多少钱。
思路: 这个题目是我们知道了结果,需要逆推条件, 第48月富三代要连本带息的把3k一把取走,那么
第47月存款应为: (第48个月的存款+3000)/(1+0.0171/12(月));
第46月存款应为: (第47个月的存款+3000)/(1+0.0171/12(月));
..... .....
第1个月存款应为: (第2个月的存款+3000)/(1+0.0171/12(月));
//银行取钱问题
double[] month = new double[49];
///最后一个月的连本带息是3000
month[48] = 3000;
double rate = 0.0171;
//逆推
for (int i = 47; i > 0; i--)
{
month[i] = (month[i + 1] + month[48]) / (1 + rate / 12);
}
for (int i = 48; i > 0; i--)
{
Console.WriteLine("第{0}个月末本利合计:{1}", i, month[i]);
}
转自 一线码农
