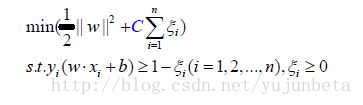R语言与机器学习学习笔记（分类算法）（4）支持向量机

算法四：支持向量机

       说到支持向量机，必须要提到july大神的《支持向量机通俗导论》，个人感觉再怎么写也不可能写得比他更好的了。这也正如青莲居士见到崔颢的黄鹤楼后也只能叹“此处有景道不得”。不过我还是打算写写SVM的基本想法与libSVM中R的接口。

一、SVM的想法

       回到我们最开始讨论的ＫＮＮ算法，它占用的内存十分的大，而且需要的运算量也非常大。那么我们有没有可能找到几个最有代表性的点（即保留较少的点）达到一个可比的效果呢？

       要回答这个问题，我们首先必须思考如何确定点的代表性？我想关于代表性至少满足这样一个条件：无论非代表性点存在多少，存在与否都不会影响我们的决策结果。显然如果仍旧使用KNN算法的话，是不会存在训练集的点不是代表点的情况。那么我们应该选择一个怎样的“距离”满足仅依靠代表点就能得到全体点一致的结果？

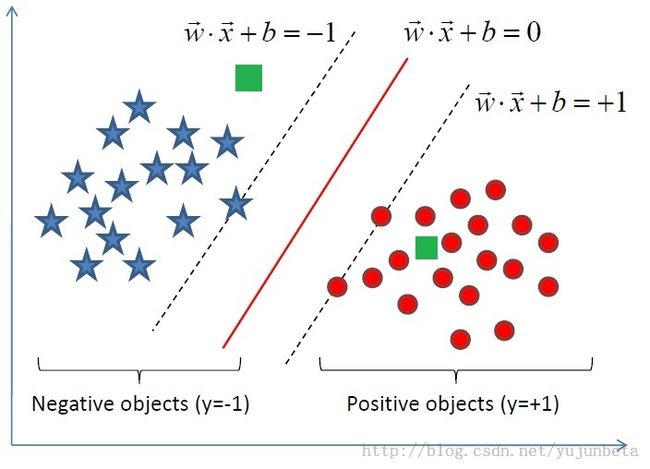
       我们先看下面一个例子：假设我们的训练集分为正例与反例两类，分别用红色的圆圈与蓝色的五角星表示，现在出现了两个未知的案例，也就是图中绿色的方块，我们如何去分类这两个例子呢？

         在KNN算法中我们考虑的是未知样例与已知的训练样例的平均距离，未知样例与正例和反例的“距离”谁更近，那么他就是对应的分类。

        同样是利用距离，我们可以换一个方式去考虑：假设图中的红线是对正例与反例的分类标准（记为w ∙ x+b=0），那么我们的未知样例与红线的“距离”就成了一个表示分类信度的标准，而w ∙ y+b（y为未知样例的数据）的符号则可以看成是分类的标识。

        但是遗憾的是我们不知道这样的一条分类标准（分类线）是什么，那么我们一个比较自然的想法就是从已知的分类数据（训练集）里找到离分割线最近的点，确保他们离分割面尽可能的远。这样我们的分类器会更稳健一些。

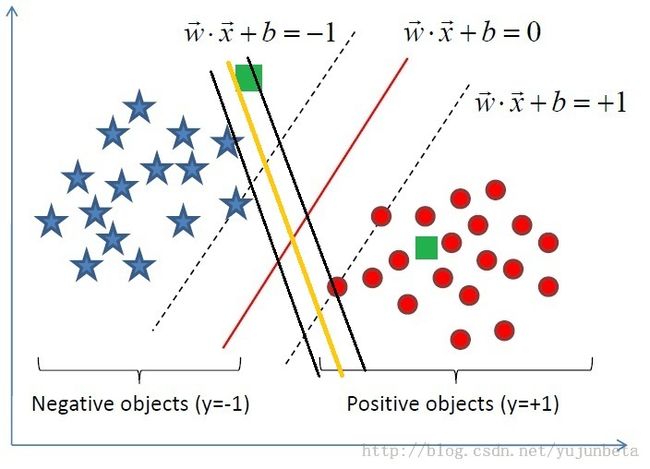
      从上面的例子来看，虚线穿过的样例便是离分割线最近的点，这样的点可能是不唯一的，因为分割线并不确定，下图中黑线穿过的训练样例也满足这个要求：

        所以“他们离分割面尽可能的远”这个要求就十分重要了，他告诉我们一个稳健的超平面是红线而不是看上去也能分离数据的黄线。

       这样就解决了我们一开始提出的如何减少储存量的问题，我们只要存储虚线划过的点即可（因为在w ∙ x+b=-1左侧，w ∙ x+b=1右侧的点无论有多少都不会影响决策）。像图中虚线划过的，距离分割直线（比较专业的术语是超平面）最近的点，我们称之为支持向量。这也就是为什么我们这种分类方法叫做支持向量机的原因。

        至此，我们支持向量机的分类问题转化为了如何寻找最大间隔的优化问题。

二、SVM的一些细节

       支持向量机的实现涉及许多有趣的细节：如何最大化间隔，存在“噪声”的数据集怎么办，对于线性不可分的数据集怎么办等。

       我这里不打算讨论具体的算法，因为这些东西完全可以参阅july大神的《支持向量机通俗导论》，我们这里只是介绍遇到问题时的想法，以便分析数据时合理调用R中的函数。

      几乎所有的机器学习问题基本都可以写成这样的数学表达式：

• 给定条件：n个独立同分布观测样本(x1 , y1 ), (x2 , y2 ),……,(xn , yn )
• 目标：求一个最优函数f (x,w* )
• 最理想的要求：最小化期望风险R（w）

       不同的是我们如何选择f,R。对于支持向量机来说，f(x,w*)=w∙ x+b，最小化风险就是最大化距离|w ∙x|/||w||，即arg max{min（label ∙（w ∙x+b））/||w||}  (也就是对最不confidence 的数据具有了最大的 confidence)

       这里的推导涉及了对偶问题，拉格朗日乘子法与一堆的求导，我们略去不谈，将结果叙述如下：

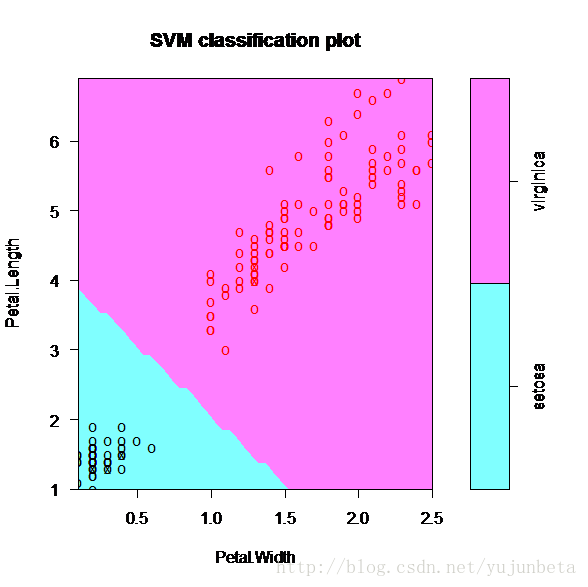
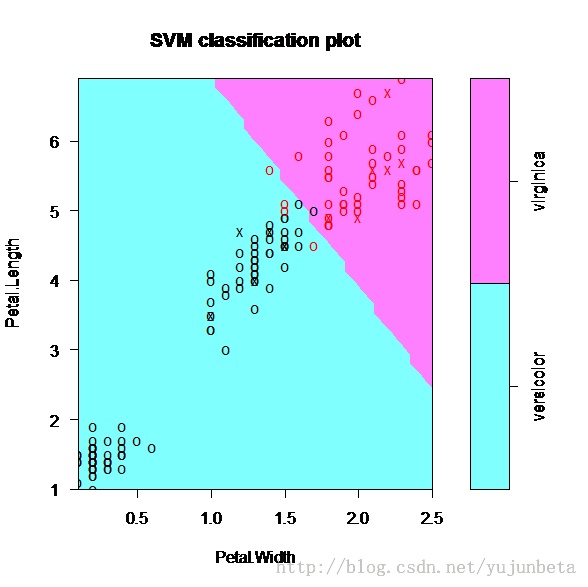
        我们以鸢尾花数据来说说如何利用svm做分类，由于svm是一个2分类的办法，所以我们将鸢尾花数据也分为两类，“setosa”与“versicolor”（将后两类均看做一类），那么数据按照特征：花瓣长度与宽度做分类，有分类：

         从上图可以看出我们通过最优化原始问题或者对偶问题就可以得到w,b，利用     sign（w.x+b）就可以判断分类了。

         我们这里取3, 10,56, 68,107, 120号数据作为测试集，其余的作为训练集，我们可以看到：

训练集    setosa    virginica

  setosa        48        0        

  virginica       0        96

测试集     setosa    virginica

  setosa         2        0   

  virginica       0       4

        也就是完全完成了分类任务。

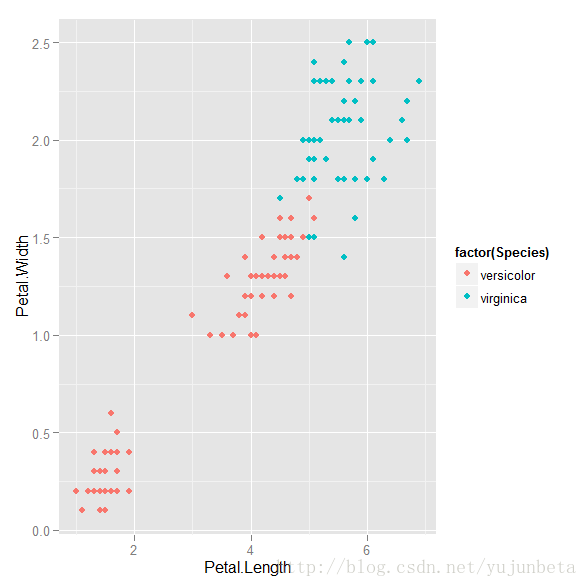
        我们来看看鸢尾花后两类的分类versicolor和virginica的分类，我们将数据的散点图描绘如下：（我们把第一类“setosa“看做”versicolor“）

        不难发现这时无论怎么画一条线都无法将数据分开了，那么这么办呢？我们一个自然的办法就是允许分类有一部分的错误，但是错误不能无限的大。我们使用一个松弛项来分类数据。最优化问题转变为：

       当我们确定好松弛项C后，就可以得到分类：

 

           我们还是先来看看分类的效果：（C=10）

训练集    versicolor     virginica

  versicolor         93         2

  virginica           3        46

    测试集     versicolor    virginica

  versicolor          4        2

  virginica           0         0

         虽然分类中有一些错误，但是大部分还是分开了的，也就是说还是不错的，至少完成了分类这个任务。

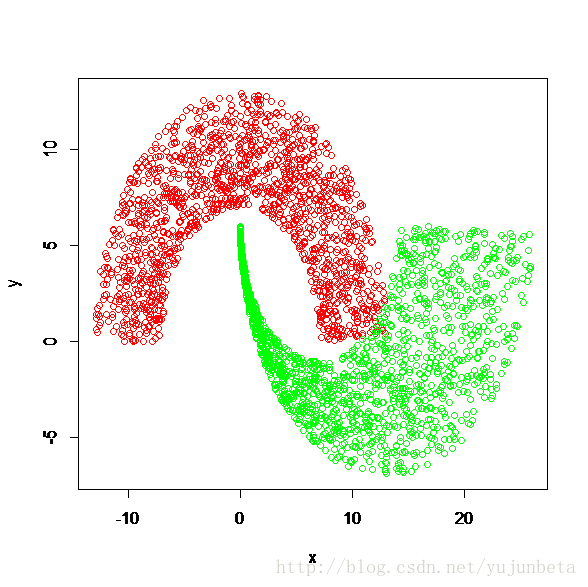
         我们再来看看一个更麻烦的例子：

         假设数据是这样的：

       这时再用直线作为划分依据就十分的蹩脚了，我们这时需要引入核的方法来解决这个问题。

        在上图中，我们一眼就能看出用一个S型去做分类就可以把数据成功分类了（当然是在允许一点点错误的情况下），但是计算机能识别的只有分类器的分类结果是-1还是1，这时，我们需要将数据做出某种形式的转换，使得原来不可用直线剖分的变得可分，易分。也就是需要找到一个从一个特征空间到另一个特征空间的映射。我们常用的映射有：

• 线性核:u'*v
• 多项式核:(gamma*u'*v+ coef0)^degree
• 高斯核:exp(-gamma*|u-v|^2)
• Sigmoid核:tanh(gamma*u'*v + coef0)

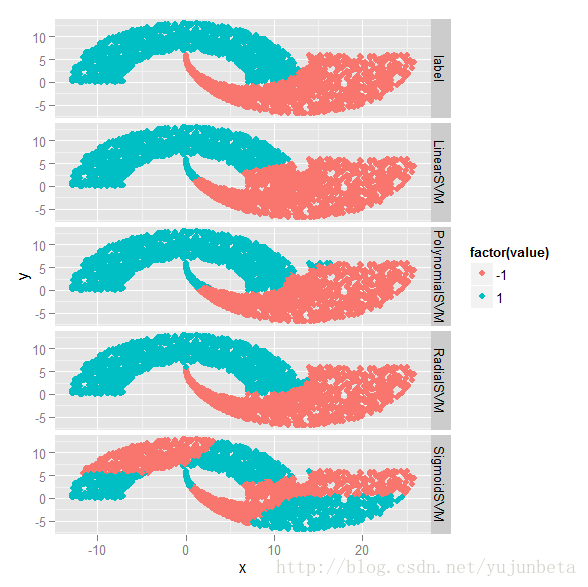
     我们这里使用各种常见的核来看看分类效果：

         从图中我们可以看到正态核的效果是最好的,用数据说话，我们来看看分类错误率与折10交叉验证的结果（报告平均分类正确率）：

        我们可以看到，无论从存储数据量的多少（支持向量个数）还是分类精确度来看，高斯核都是最优的。所以一般情况，特别是在大样本情况下，优先使用高斯核，至少可以得到一个不太坏的结果(在完全线性可分下，线性函数的支持向量个数还是少一些的)。

三、libSVM的R接口

      有许多介绍SVM的书都有类似的表述“由于理解支持向量机需要掌握一些理论知识，而这对读者来说有一定的难度，建议直接下载LIBSVM使用。”

        确实，如果不是为了训练一下编程能力，我们没有必要自己用前面提到的做法自己实现一个效率不太高的SVM。R的函数包e1071提供了libSVM的接口，使用e1071的函数SVM（）可以得到libSVM相同的结果，write.svm（）更是可以把R训练得到的结果写为标准的libSVM格式供其他环境下的libSVM使用。

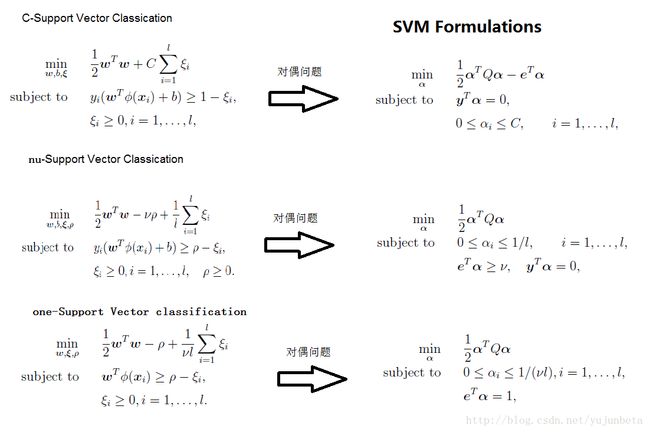
       在介绍R中函数的用法时，我们先简要介绍一下SVM的类型，以便我们更好地理解各个参数的设置。

         对于线性不可分时，加入松弛项，折衷考虑最小错分样本和最大分类间隔。增加了算法的容错性，允许训练集不完全分类，以防出现过拟合。加入的办法有以下3类，写成最优化问题形式总结如上图：

       上图中e为所有元素都为1的列向量，Qij=yiyjK(xi; xj), K(xi; xj) =phi(xi) ∙phi (xj), phi(.)为核函数，K（. ；.）表示对应元素核函数的内积。

       现在我们来看看svm（）函数的用法。

## S3 method for class 'formula'

svm(formula, data = NULL, ..., subset,na.action =na.omit, scale = TRUE)

## Default S3 method:

svm(x, y = NULL, scale = TRUE, type = NULL,kernel =

"radial", degree = 3, gamma = if(is.vector(x)) 1 else 1 / ncol(x),

coef0 = 0, cost = 1, nu = 0.5,

class.weights = NULL, cachesize = 40,tolerance = 0.001, epsilon = 0.1,shrinking = TRUE, cross = 0, probability =FALSE, fitted = TRUE, seed = 1L,..., subset, na.action = na.omit)

       主要参数说明：

Formula：分类模型形式，在第二个表达式中使用的的x，y可以理解为y~x。

Data：数据集

Subset：可以指定数据集的一部分作为训练集

Na.action：缺失值处理，默认为删除数据条目

Scale：将数据标准化，中心化，使其均值为0，方差为1.默认自动执行。

Type：SVM的形式，使用可参见上面的SVMformulation，type的选项有：C-classification，nu-classification，one-classification (for novelty detection)，eps-regression，nu-regression。后面两者为利用SVM做回归时用到的，这里暂不介绍。默认为C分类器，使用nu分类器会使决策边界更光滑一些，单一分类适用于所有的训练数据提取自同一个类里，然后SVM建立了一个分界线以分割该类在特征空间中所占区域和其它类在特征空间中所占区域。

Kernel：在非线性可分时，我们引入核函数来做非线性可分，R提供的核介绍如下：

• 线性核:u'*v
• 多项式核:(gamma*u'*v + coef0)^degree
• 高斯核:exp(-gamma*|u-v|^2)
• Sigmoid核:tanh(gamma*u'*v + coef0)

      默认为高斯核（RBF），libSVM的作者对于核的选择有如下建议：Ingeneral we suggest you to try the RBF kernel first. A recent result by Keerthiand Lin shows that if RBF is used with model selection, then there is no need to consider the linear kernel. The kernel matrix using sigmoid may not be positive definite and in general it's accuracy is not better than RBF. (see thepaper by Lin and Lin. Polynomial kernels are ok but if a high degree is used,numerical difficulties tend to happen (thinking about dth power of (<1) goes to 0 and (>1) goes to infinity).

顺带说一句，在kernlab包中，可以自定义核函数。

Degree:多项式核的次数，默认为3

Gamma:除去线性核外，其他的核的参数，默认为1/数据维数

Coef0,：多项式核与sigmoid核的参数，默认为0

Cost：C分类的惩罚项C的取值

Nu：nu分类，单一分类中nu的取值

Cross：做K折交叉验证，计算分类正确性。

       由于svm的编程确实过于复杂，还涉及到不少最优化的内容，所以在第二部分我的分类都是使用svm函数完成的（偷一下懒），现将部分R代码展示如下：

dataSim的函数：

simData=function(radius,width,distance,sample_size)
{
   aa1=runif(sample_size/2)
   aa2=runif(sample_size/2)
  rad=(radius-width/2)+width*aa1
   theta=pi*aa2
   x=rad*cos(theta)
   y=rad*sin(theta)
   label=1*rep(1,length(x))
 
   x1=rad*cos(-theta)+rad
   y1=rad*sin(-theta)-distance
   label1=-1*rep(1,length(x1))
 
   n_row=length(x)+length(x1)
   data=matrix(rep(0,3*n_row),nrow=n_row,ncol=3)
   data[,1]=c(x,x1)
   data[,2]=c(y,y1)
   data[,3]=c(label,label1)
  
   data
  
}
dataSim=simData(radius=10,width=6,distance=-6,sample_size=3000)
colnames(dataSim)<-c("x","y","label")
dataSim<-as.data.frame(dataSim)

Sigmoid核的分类预测：

m1 <- svm(label ~x+y, data =dataSim,cross=10,type="C-classification",kernel="sigmoid")
m1
summary(m1)
pred1<-fitted(m1)
table(pred1,dataSim[,3])

核函数那一小节作图的各种东西：

linear.svm.fit <- svm(label ~ x + y, data = dataSim, kernel ='linear')
with(dataSim, mean(label == ifelse(predict(linear.svm.fit) > 0,1, -1)))
 
polynomial.svm.fit <- svm(label ~ x + y, data = dataSim, kernel ='polynomial')
with(dataSim, mean(label == ifelse(predict(polynomial.svm.fit) >0, 1, -1)))
 
radial.svm.fit <- svm(label ~ x + y, data = dataSim, kernel ='radial')
with(dataSim, mean(label == ifelse(predict(radial.svm.fit) > 0,1, -1)))
 
sigmoid.svm.fit <- svm(label ~ x + y, data = dataSim, kernel ='sigmoid')
with(dataSim, mean(label == ifelse(predict(sigmoid.svm.fit) > 0,1, -1)))
 
df <- cbind(dataSim,
           data.frame(LinearSVM = ifelse(predict(linear.svm.fit) > 0, 1, -1),
                      PolynomialSVM = ifelse(predict(polynomial.svm.fit) > 0, 1, -1),
                      RadialSVM = ifelse(predict(radial.svm.fit) > 0, 1, -1),
                      SigmoidSVM = ifelse(predict(sigmoid.svm.fit) > 0, 1, -1)))
library("reshape")
predictions <- melt(df, id.vars = c('x', 'y'))
library('ggplot2')
ggplot(predictions, aes(x = x, y = y, color = factor(value))) +
  geom_point() +
  facet_grid(variable ~ .)

           最后，我们回到最开始的那个手写数字的案例，我们试着利用支持向量机重做这个案例。（这个案例的描述与数据参见《R语言与机器学习学习笔记（分类算法）（1）》）

运行代码：

setwd("D:/R/data/digits/trainingDigits")
names<-list.files("D:/R/data/digits/trainingDigits")
data<-paste("train",1:1934,sep="")
for(i in 1:length(names))
         assign(data[i],as.vector(as.matrix(read.fwf(names[i],widths=rep(1,32)))))
label<-rep(0:9,c(189,198,195,199,186,187,195,201,180,204))
 
data1<-get(data[1])
for(i in 2:length(names))
         data1<-rbind(data1,get(data[i]))
 
m <- svm(data1,label,cross=10,type="C-classification")
m
summary(m)
pred<-fitted(m)
table(pred,label)
 
setwd("D:/R/data/digits/testDigits")
names<-list.files("D:/R/data/digits/testDigits")
data<-paste("train",1:1934,sep="")
for(i in 1:length(names))
         assign(data[i],as.vector(as.matrix(read.fwf(names[i],widths=rep(1,32)))))
data2<-get(data[1])
for(i in 2:length(names))
         data2<-rbind(data2,get(data[i]))
pred<-predict(m,data2)
labeltest<-rep(0:9,c(87,97,92,85,114,108,87,96,91,89))
table(pred,labeltest)

模型摘要：

Call:

svm.default(x = data1, y = label, type ="C-classification",  cross =10)

Parameters:

   SVM-Type:  C-classification

 SVM-Kernel:  radial

       cost:  1

      gamma:  0.0009765625

Number of Support Vectors: 1139     ( 78 130 101 124 109 122 87 93 135 160 )

Number of Classes:  10

Levels:  0 1 2 3 4 5 6 7 8 9

10-fold cross-validation on training data:

Total Accuracy: 96.7425

Single Accuracies:

 97.40933 98.96373 91.7525899.48187 94.84536 94.30052 97.40933 96.90722 98.96373 97.42268

        当然，我们还可以通过m$SV查看支持向量的情况，m$index查看支持向量的标签，m$rho查看分类时的截距b。

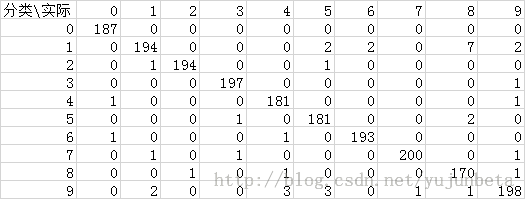
训练集分类结果：

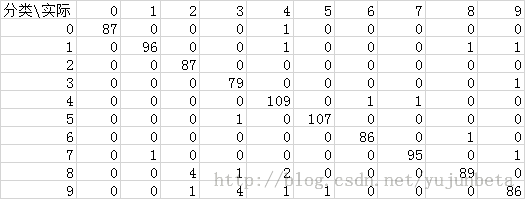
我们拿测试数据来看：

       分类正确率为：0.9735729，误差率为2.6%左右，确实达到了开篇提出的可比的目的，而需要储存的支持向量个数仅为1139个，比原来的训练数据1934个要少了近50%，也达到了我们要求的节约存储的目的。当然值得一提的是线性分类的效果在实际中也没有那么糟糕，可以牺牲线性核函数的正确率来换取分类速度与存储空间。另外，支持向量的个数与训练集的出错率也没有特别必然的联系，而是与容错率cost有一定的联系。

FurtherReading:

在R中使用支持向量机：(3.e1071包和klaR包)

支持向量机: Maximum MarginClassifier

预告

        本文之后，待写的几篇文章罗列如下：

• 算法五：神经网络
• 算法六：logistic回归

 （to be continue）

    最后说一句，临近期末，各种考试来袭，12月更新最后两个算法基本是不可能了。