关于聚类

1 聚类的类型

     聚类可以通过人工神经网络来实现，也可以通过专门的聚类算法实现，例如参考资料[3]介绍了较为常见的k-means、层次聚类、SOM以及FCM四种聚类算法，其中SOM属于神经网络方法。本文重点介绍层次聚类算法。

    参考资料[3]提到，根据层次分解的顺序是自底向上的还是自上向下的，层次聚类算法又可分为凝聚的层次聚类算法和分裂的层次聚类算法，本文主要介绍前者。

2 凝聚层次聚类算法

    参考资料[9]解析了凝聚层次聚类的含义：所谓凝聚的，指的是该算法初始时，将每个点作为一个簇，每一步合并两个最接近的簇。例如：依次取当前最近的点对，如果这个点对当前不在一个簇中，则将这两个点所在的两个簇合并。另外即使到最后，对于噪音点或是离群点也往往还是各占一簇的，除非过度合并。对于这里的"最接近"，有下面三种定义：

    (1)单链(MIN)：定义簇的邻近度为不同两个簇的两个最近的点之间的距离。
    (2)全链(MAX)：定义簇的邻近度为不同两个簇的两个最远的点之间的距离。
    (3)组平均：定义簇的邻近度为取自两个不同簇的所有点对邻近度的平均值。

    参考资料[3]对凝聚型层次聚类的策略也作了类似的介绍：先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到所有对象都在一个簇中，或者某个终结条件被满足。绝大多数层次聚类属于凝聚型层次聚类，它们只是在簇间相似度的定义上有所不同。四种广泛采用的簇间距离度量方法如下：

    参考资料[3]给出采用最小距离的凝聚层次聚类算法流程：

　(1) 将每个对象看作一类，计算两两之间的最小距离；
　(2) 将距离最小的两个类合并成一个新类；
　(3) 重新计算新类与所有类之间的距离；
　(4) 重复(2)、(3)，直到所有类最后合并成一类。

3 凝聚层次聚类的matlab实现

    参考资料[8]介绍了matlab中实现凝聚层次聚类的两种方法：a)一次聚类；b)分步聚类。本文重点介绍后者。

3.1 使用pdist计算变量之间的距离

    关于pdist，matlab帮助文档的解析如下：

pdist
Pairwise distance between pairs of objects
Syntax
D = pdist(X)
D = pdist(X,distance)
D = pdist(X) computes the Euclidean distance between pairs of objects in m-by-n data matrix X. 
Rows of X correspond to observations, and columns correspond to variables. 
D is a row vector of length m(m–1)/2,corresponding to pairs of observations in X.

    根据上述的解析可知，pdist主要的作用是计算X矩阵中行与行之间的距离。

3.2 用linkage函数来产生聚类树

    matlab帮助文档中对linkage的解析如下：

linkage
Agglomerative hierarchical cluster tree
Syntax
Z = linkage(X)
Z = linkage(X,method)

Description
Z = linkage(X) returns a matrix Z that encodes a tree of hierarchical clusters of the rows of the real matrix X.
Z = linkage(X,method) creates the tree using the specified method, where method describes how to measure the distance between clusters.

    实例

clear
clc
X = [1
     2
     3];
Y = pdist(X, 'euclidean');
Z = linkage(Y, 'average');
dendrogram(Z);

   运算结果如下

Y = [1  2  1]

Z =  [2	   3	1
      1	   4	1.5]

    解析：Y的三个值分别为X(1)vsX(2)，X(1)vsX(3)以及X(2:)vsX(3)。

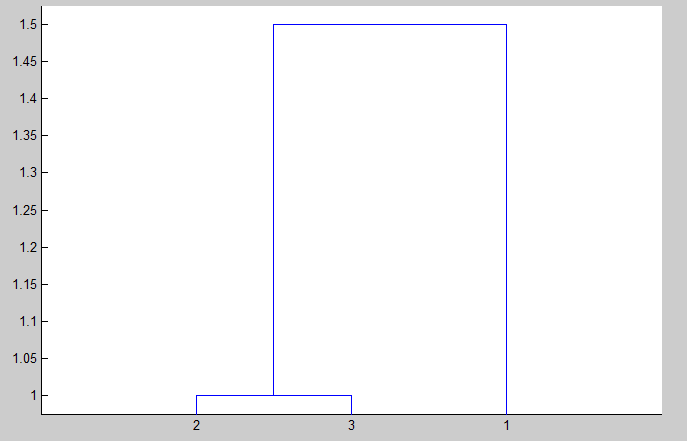
                Z的第1行表示X(2)与X(3)的距离为1，聚为一类，新一类命名为4；

                Z的第2行表示X(1)与新产生的类4的距离为1.5，聚为一类（其距离其实是X(1)vsX(2)的距离1和X(1)vsX(3)的距离2的平均值)。

    dendrogram将层次聚类树画为如下图：

3.3 用 cluster进行聚类，返回聚类列

    matlab帮助文档中关于cluster的说明如下

cluster
Construct agglomerative clusters from linkages
Syntax
T = cluster(Z,'cutoff',c)
T = cluster(Z,'cutoff',c,'depth',d)
T = cluster(Z,'cutoff',c,'criterion',criterion)
T = cluster(Z,'maxclust',n)

Description
T = cluster(Z,'cutoff',c) constructs clusters from the agglomerative hierarchical cluster tree, Z,
as generated by the linkage function. Z is a matrix of size (m – 1)-by-3, where m is the number of observations in the original data. c is
a threshold for cutting Z into clusters. Clusters are formed when a node and all of its subnodes have inconsistent value less than c.
All leaves at or below the node are grouped into a cluster. t is a vector of size m containing the cluster assignments
of each observation.If c is a vector, T is a matrix of cluster assignments with one column per cutoff value.T = cluster(Z,'cutoff',c,'depth',d) evaluates
inconsistent values by looking to a depth d below
each node. The default depth is 2.
T = cluster(Z,'cutoff',c,'criterion',criterion) uses the specified criterion for forming clusters, where criterion is
one of the strings 'inconsistent' (default) or 'distance'.The 'distance' criterion uses the distance between
the two subnodes merged at a node to measure node height. All leaves at or below a node with height less than c are
grouped into a cluster.
T = cluster(Z,'maxclust',n) constructs a maximum of n clusters using  the 'distance' criterion. cluster finds
the smallest height at which a horizontal cut through the tree leaves n or fewer clusters.If n is a vector, T is
a matrix of cluster assignments with one column per maximum value.

    实例

    在上面的实例的基础上，利用cluster对Z进行构建

T = cluster(Z, 2);

    上面的命令意思为：将Z进行归类，类别最大为2。结果如下

T=[1

      2

      2];

    也就是说，X(1)是一类，X(2)和X(3)归为一类。

参考资料

[1]聚类

[2]一种改进的凝聚层次聚类法

[3]四种聚类方法之比较

[4]基于凝聚的层次聚类算法的改进

[5]用MATLAB做聚类分析

[6]用matlab做聚类分析

[7]matlab聚类分析

[8]用matlab做聚类分析 

[9]初识聚类算法:K均值、凝聚层次聚类和DBSCAN