数据结构与算法8: 二叉搜索树遍历算法(Binary search tree traversing algorithm)
写在前面
二叉树是应用广泛的一类树,通过学习二叉搜索树(BST)、平衡二叉树(AVL)、伸展树(Splay Tree)以及二叉堆(Binary Heap)的相关概念、操作以及分析算法性能,对理解树有很大帮助。本节总结和实现二叉搜索树遍历的基本方法,包括深度优先遍历和广度优先遍历。建议时间充足的初学者,自己动手全部实现一遍代码,必定会获得很大的收益。笔者在此过程中获益良多,注意思考:
深度优先遍历的方法(递归实现,借助栈的非递归实现,在遍历过程中修改和恢复树结构的Morris算法,以及线索二叉树的实现)的联系与区别
广度优先算法借助队列的思想
-
- 广度优先遍历Breadth first traversing
- 深度优先遍历Depth first traversing
- 1 递归实现
- 2 借助栈的实现
- 先序遍历
- 中序遍历
- 后序遍历
- 3 修改和恢复树结构的Morris实现
- 4 线索二叉树实现遍历
- 总结
1 广度优先遍历(Breadth first traversing)
广度优先遍历是树和图遍历的一种常见方法,对于树而言,规则是从根节点开始,从上到下,从左到右访问树中节点。先被访问的顶点的孩子节点要先于后被访问的顶点的孩子节点。
算法思想:
根节点入队列;队头元素出队列,并将对头元素的非空左孩子和右孩子依次入队列,持续这个过程直到队列为空。
具体实现如下:
/** * 宽度优先搜索 * 遍历顺序为从上到下,从左到右 * 借助队列实现 */
void BST::breadthFirst() const{
if(root == 0) return;
queue<const BSTNode*> nodeQueue;// 指针队列
nodeQueue.push(root);
const BSTNode* current = 0;
while(!nodeQueue.empty()) {
current = nodeQueue.front();
nodeQueue.pop();
visit(current);
if(current->left != 0)
nodeQueue.push(current->left);// 非空左孩子入队列
if(current->right != 0)
nodeQueue.push(current->right);// 非空右孩子入队列
}
}其中visit函数为访问结点函数,默认实现为:
virtual void visit(const BSTNode *p) const{ //子类按需实现
if(bshowVisitInfo)
std::cout << p->key << "(height=" << p->height << ")\t";
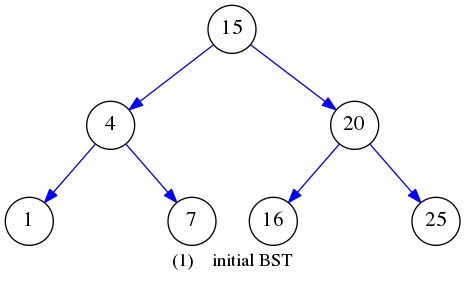
}给定二叉搜索树如下:
广度优先遍历结果如下:
2 深度优先遍历(Depth first traversing)
深度优先遍历将尽可能地向左(或者向右)发展,在遇到第一个转折点时,向右(或者向左)一步,然后,再尽可能地向左(或者向右)发展。持续这一过程,直到访问了所有的节点为止。
在访问过程中有三个子任务即:
V 访问根节点
L 遍历左子树
R 遍历右子树
根据排列组合知识共有3!=6种方式,规定总是先遍历左子树,再遍历右子树,即按照先L后R方式,一共有三种情况:
VLR 先序遍历
LVR 中序遍历
LRV 后序遍历
先序遍历VLR结果入下图所示:
中序遍历结果LVR如下图所示:
后序遍历LRV结果如下图所示:
对于深度优先遍历可以有多种实现方式,下面分别学习。
重点关注借助栈实现以及Morris算法。
2.1 递归实现
递归实现的版本思想很简单,不再赘述,例如中序遍历实现如下:
/** * 递归实现的中序遍历 * 遍历顺序为LVR */
void BST::inorder(const BSTNode* p) const{
if(p != 0) {
inorder(p->left);
visit(p);
inorder(p->right);
}
}
void inorder() const{
inorder(root);
}2.2 借助栈的实现
借助栈实现时,针对不同遍历需要付出不同的努力。利用栈实现遍历的关键点是:通过观察遍历方式,找到遍历的规律。利用这个规律借助栈来实现。
以下部分,建议你拿出草稿纸,在草稿上进行树和栈的演算,这样能更好的理解。
先序遍历
先序遍历的特点是,每个节点总是先访问根结点,然后先序访问左孩子,再先序访问右孩子。我们可以在访问完根节点后,依次将右孩子根节点、左孩子根节点入栈,然后出栈,访问栈顶元素,对栈顶元素重复这个过程即可完成先序遍历。
代码实现为:
/** * 非递归实现的先序遍历 * 遍历顺序为VLR * 借助栈实现 * 算法思想: * 1) 树为空则退出,否则根节点入栈 * 2) 访问栈顶元素v,出栈,元素v的右孩子入栈,元素v的左孩子入栈 * 3) 持续2直到栈为空停止 */
void BST::iterativePreorder() const{
if(root == 0) return;
stack<const BSTNode*> nodeStack;
nodeStack.push(root);
const BSTNode* current = 0;
while(!nodeStack.empty()) {
current = nodeStack.top();
nodeStack.pop();
visit(current);
if(current->right != 0)
nodeStack.push(current->right); // 非空右孩子入栈
if(current->left != 0)
nodeStack.push(current->left); // 非空左孩子入栈
}
}中序遍历
中序遍历比先序遍历稍微复杂一点。基本思想是,LVR遍历时总是首先访问最左边孩子,我们把从一个结点出发寻找最左边孩子的操作起个非正式名字,叫做”归左操作”。
那么,中序遍历的算法,就是首先对根进行归左操作,这个过程中的结点都入栈,直到入栈结点没有左孩子为止,从这个孩子开始出栈(因为LVR,没有了L则可以直接访问结点本身V),出栈时即访问该结点;持续出栈,直到这个出栈的结点,有右孩子为止,对右孩子进行归左操作,重复这样的过程,直到没有待归左操作的结点为止。
实现代码如下:
/** * 非递归实现的中序遍历 * 遍历顺序为LVR * 借助栈实现 * 算法思想: * 1) 树为空则退出,否则current = root,其中current为待寻找最左边孩子的结点 * 2) 循环查找current的最左孩子结点,直到左孩子为空,此过程中结点都入栈 * 3) 取栈顶元素v,出栈,持续这个过程直到v存在右孩子时,将v的右孩子赋值给current,转到过程2 * 4) 当current 不为空时,持续步骤2和3 */
void BST::iterativeInorder() const{
if(root == 0) return;
stack<const BSTNode *> nodeStack;
const BSTNode* current = root;
const BSTNode* top = 0;
while(current != 0) {
// 寻找最左边孩子
while(current != 0) {
nodeStack.push(current);
current = current->left;
}
// 访问栈顶并出栈 直至找到下一个待寻找最左边孩子的节点
while(!nodeStack.empty() && current == 0) {
top = nodeStack.top();
nodeStack.pop();
visit(top);
current = top->right;
}
}
}后序遍历
后序遍历比中序遍历稍微复杂一点。思想基本与中序遍历相同,同样执行”归左操作”,不同之处在于执行“归左操作”完毕的结点,并不能立即访问(因为LRV中即使没有了L,还需要先对R进行后序遍历),必须判断这个结点有没有右孩子,如果有的话,对右孩子也要执行“归左操作”。
算法思想是,以根节点为开始待“归左”结点,归左过程中持续入栈;接下来判断栈顶元素,如果栈顶没有右孩子(top->right == 0)或者右孩子已经访问过(top->right == prev)则直接访问这个栈顶,否则对栈顶元素的右孩子进行“归左操作”。持续这个过程直到没有待“归左”的结点为止。
注意,访问的过程中对出栈结点,都要使用prev记录下来,以便于后续的判断。
实现如下:
/** * 非递归实现的后续遍历 * 遍历顺序为LRV * 借助栈实现 * 算法思想: * 1) 树为空则退出,否则current = root,其中current为待寻找最左边孩子的结点 * 2) 循环查找current的最左孩子结点,直到左孩子为空,此过程中结点都入栈 * 3) 当栈不空并且current为空时,取栈顶元素v * 如果v没有右孩子或者v的右孩子刚刚访问过(用prev指针判断) * 则将v出栈,访问v,用prev指针记录v结点,current赋值为空; * 否则 v的右孩子赋给current,转步骤2 * 4) 当current不为空时,持续步骤2和3 */
void BST::iterativePostorder() const{
if(root == 0) return;
stack<const BSTNode*> nodeStack;
const BSTNode* current = root;
const BSTNode* prev = 0,*top = 0;
while(current != 0) {
// 寻找最左边孩子
while(current != 0) {
nodeStack.push(current);
current = current->left;
}
while(!nodeStack.empty() && current == 0) {
top = nodeStack.top();
// 没有右孩子或右孩子刚访问过
if(top->right == 0 || top->right == prev) {
nodeStack.pop();
visit(top);
prev = top; // 出栈结点用prev记录下来
current = 0;
}else { // 右孩子为待寻找最左边孩子的结点
current = top->right;
}
}
}
}2.3 修改和恢复树结构的Morris实现
与递归和借助栈实现的迭代算法都不同,Joseph M.Morris开发的算法,可以应用于中序遍历。这个算法在遍历树的过程中临时修改和恢复树的结构,使正在处理的结点没有左子节点,同时保证在遍历完毕后树形保持与遍历前相同。
Morris算法的核心就是建立和解除临时父子关系,来达到访问的结点无左孩子的效果。
算法思想: 当前结点p初值为root;
当p不为空时,如果当前结点没有左孩子则直接访问该结点,并把右孩子置为当前结点,继续循环;否则将当前结点的左孩子的最右边孩子置为tmp(寻找过程中遇到右孩子为空,或者右孩子就是当前结点的情况时停止)。如果tmp的右孩子为空,则建立临时父子关系(将tmp右孩子置为当前结点,并让当前结点的左孩子成为当前结点,继续循环),否则解除临时父子关系(tmp的右孩子置为空,访问当前结点,并让当前结点的右孩子成为当前结点,继续循环)。
运行过程如下图所示(截取自参考资料:《Data Structures and Algorithms in C++》 Adam Drozdek [Fourth Edition]):
算法实现如下:
/** * Joseph M. Morris 中序遍历算法 * 遍历顺序LVR * 不使用递归和栈实现的遍历算法 * 在遍历过程中修改和恢复树结构的方法 * 算法思想: * 1) 如果树为空则返回,否则current = root,current表示当前结点 * 2) 对于每个current * 如果current左孩子为空,则访问current,并将其右孩子赋给current * 否则: * 迭代取current的左孩子的最右边孩子tmp * 如果tmp是current的临时父节点,则访问current并解除临时父子关系,并将current右孩子赋给current * 否则将tmp置为current的临时父节点,并将current的左孩子赋给current * 3) 持续2过程直到current为空 */
void BST::MorrisInorder() {
if(root == 0) return;
BSTNode* current = root,*tmp = 0;
while(current != 0) {
if(current->left == 0) {
visit(current);
current = current->right;
}else {
tmp = current->left;
while(tmp->right !=0 && tmp->right != current)
tmp = tmp->right;
if(tmp->right == 0) {// tmp成为current的临时父节点
tmp->right = current;
current = current->left;
}else { // 解除tmp与current结点之间的临时父子关系
visit(current);
tmp->right = 0;
current = current->right;
}
}
}
}2.4 线索二叉树实现遍历
线索二叉树不作为重点,了解即可。
通过在结点中引入线索,可以使栈成为树的一部分,这样也可以方便进行树的遍历。所谓线索,就是当一个结点的孩子为空时,从而利用孩子指针指向前驱或者后继的指针。这是对左右孩子指针的一种重载,利用它们来指针前驱与后继,这样在遍历过程中可以利用这个指针来方便遍历。
线索二叉树可以实现为一个线索的,也可以实现为两个线索的。
其结点定义如下:
template<typename T>
class BiThreadedNode {
public:
BiThreadedNode(T k,BiThreadedNode<T>*l=0,BiThreadedNode* r=0) {
key = k;
left = l;
right = r;
successor = 0; // 0 represents not thread ,but link
}
public:
T key;
bool successor;
BiThreadedNode<T> *left,*right;
};利用线索进行中序遍历的实现如下:
template<typename T>
void BiThreadedTree<T>::inorder(){
BiThreadedNode<T> *p = root;
while(p != 0) {
while(p->left != 0 )
p = p->left;
visit(p);
while( p->successor == 1) {
visit(p->right);
p = p->right;
}
//goto right only if the node has right child
p = p->right;
}
}线索二叉树不隐式或者显式使用栈来进行树的遍历,对于中序遍历,上述代码看起来确实很简单,但它的麻烦之处在于维护线索,在插入和删除时都得进行线索的维护,在遍历之前必须保证线索是正确的。而且后序遍历版本也很复杂,这里不做深究了。
总结
本节总结的几种树遍历算法,各有特点,要么隐式使用栈(递归),要么显式使用栈,或者借助线索实现,或者在遍历过程中修改和恢复树的结构。以访问每个节点作为基本操作,可以得出这些方法的时间复杂度都为O(n)。
递归算法代码清晰,但是当遍历非常高的树时,可能会导致运行时栈溢出;
显式借助栈的算法,也可能会导致栈溢出,但没有递归那么严重;
线索树实现的遍历,必须维护线索,同时线索也得付出O(n)的多余空间来存储;
通过修改和恢复树结构的Morris遍历算法,它不需要额外的空间,这是一个优势。我觉得在多线程环境下,因为遍历时修改了树的结构,能否保证树的并发安全性是个值得考虑的问题。
在随机插入一百万和一千万个节点,然后中序遍历的比较程序中,进行实验10次,求平均值结果如下:
Inserting 10000000 nodes:
递归中序遍历平均: 23752 ms
显式借助栈的中序遍历平均: 25077 ms
Morris中序遍历平均: 22774 msInserting 1000000 nodes:
递归中序遍历平均: 2387 ms
显式借助栈的中序遍历平均: 2574 ms
Morris中序遍历平均: 2236 ms
实验结果粗略表明,运行时间,Morris算法 < 递归算法 < 迭代算法。
可以看出Morrris算法还是很有优势,而递归版本的算法性能也很好,迭代实现的版本涉及到较多的入栈和出栈操作,三者中性能排在末尾。