决策树分类
转载于:
http://funhacks.net/2015/05/05/Decision-tree/
*******************************************************
作者:FunHacks
出处:http://funhacks.net/2015/05/05/Decision-tree/
声明:本文采用以下协议进行授权 署名-非商业性使用-相同方式共享 4.0|Creative Commons BY-NC-SA 4.0 ,转载请注明作者及出处。
1. 背景
在日常生活中,当我们做决策的时候,经常会提出一系列问题,以让决策的结果能符合对方或者我们的期望。比如,现在Bill想买一台智能手机,他向朋友Martin咨询,有如下对话:
Bill: Martin,我想买一台智能手机,不知有什么可以推荐的?
Martin: 你是想要iPhone,Android还是Windows Phone的?(问题1)
Bill: Android。
Martin: 那大概想要什么价位的?(问题2)
Bill: 大概2000到3000的样子。
Martin: 好的,那你倾向于国产手机还是国外手机?(问题3)
Bill: em…国产手机。
…
Martin: OK,根据我最近的观察,给你推荐这款手机。
Bill: 谢谢,我试一下。
Bill想让Martin给他推荐手机,Martin为了了解他的需求,问了几个问题,这样才可以有针对性地进行推荐。Bill的决策可以用下面的图进行展示:
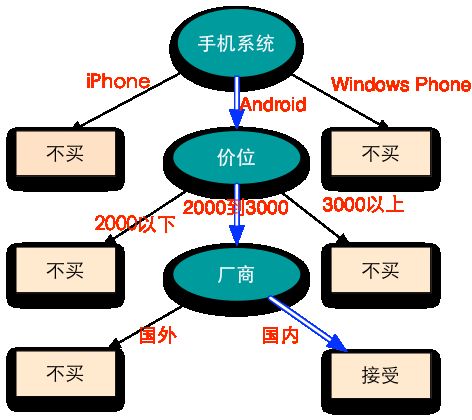
上面的树形图表示了Bill的决策过程,图中的椭圆节点是一些判断结点,矩形节点是一些决策节点,图中的蓝色箭头表示了Bill的选择,他大概想要买一台国产2000到3000的Android手机。
决策树分类跟上面的决策过程类似,通过提出一系列精心构思的测试条件(或者说判断条件),解决分类问题。每当一个问题得到答案,后续的问题将随之而来,直到我们将其归到某一类。
2. 什么是决策树
[决策树]是一种由结点和有向边组成的层次结构,树中包含三种结点:
- 根结点:它没有入边,但有零条或多条出边;
- 内部结点:恰有一条入边和两条或多条出边;
- 叶结点:恰有一条入边,但没有出边;
比如上面的决策树,手机系统是一个根结点,价位和厂商是内部结点,矩形结点都是叶结点。
在决策树中,每个叶结点都赋予一个类标号。非叶结点(包括根结点和内部结点)包含属性测试条件(比如上面的手机系统、价位和厂商就是属性测试条件),用以分开具有不同特性的记录。
这里举一个脊椎动物分类的例子(来源:《数据挖掘导论》)加以说明。假设我们要把脊椎动物分为两个类别:哺乳类动物和非哺乳类动物。我们构造如下的决策分类树:
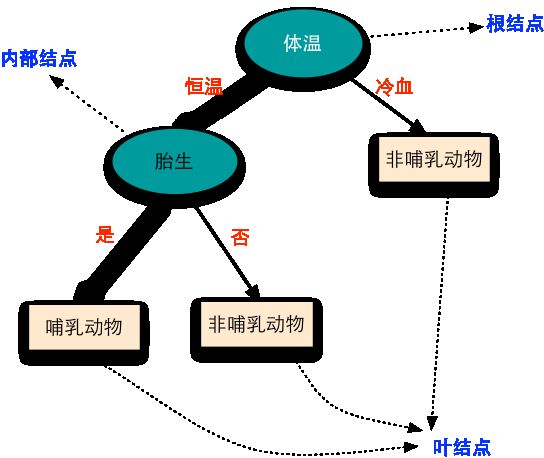
- 在根结点处,使用
体温这个属性测试条件把冷血脊椎动物和恒温脊椎动物分开; - 因为所有的冷血脊椎动物都是非哺乳动物,所以用一个类称号为
非哺乳动物的叶结点作为根结点的右子女; - 如果脊椎动物的体温是恒温的,则接下来用
胎生这个属性来区分哺乳动物和其他恒温动物
3. 如何构造决策树
原则上讲,对于给定的属性集,可以构造的决策树的数目达指数级。尽管某些决策树比其他决策树更准确,但是由于搜索空间是指数规模的,找出最佳决策树在计算上是不可行的。尽管如此,人们还是开发了一些有效的算法,能够在合理的时间内构造出具有一定准确率的次最优决策树。这些算法通常都采用贪心策略,在选择划分数据的属性时,采取一系列局部最优决策树来构造决策树。
决策树分类的学习算法必须解决下面两个问题:
- 如何分裂训练记录?树从根结点增长到叶结点过程的每个递归步都必须选择一个属性测试条件,将记录划分成较小的子集。为了实现这个步骤,算法必须提供为不同类型的属性指定测试条件的方法,并且提供评估每种测试条件的客观度量;
- 何时停止分裂?需要有结束条件,以终止决策树的生长过程。一个可能的策略是分裂结点,直到所有的记录都属于同一个类,或者所有的记录都具有相同的属性值。
其中,在分裂训练记录时,根据属性是离散的还是连续的以及是否生成二叉树,会产生以下几种情况:
- 属性是离散值且不要求生成二叉树。此时可以用每个属性值作为一个划分,比如
手机系统这个属性,有三个属性值,可分别将每个属性值作为一个划分; - 属性是离散值且要求生成二叉树。此时用属性划分的一个子集进行测试,按照属于此子集和不属于此子集分成两个分支。比如
手机系统这个属性,我们通过给出一个测试条件“是否为Windows Phone”产生两个划分,当“不是Windows Phone”时,再给出一个测试条件“是否为Android手机”,产生两个划分,这样就可以对手机进行分类了; - 属性是连续值。对于连续属性A来说,测试条件可以是具有二元输出的比较测试( A<v )或( A≥v ),也可以是一个形如 vi≤A<vi+1 的连续值区间。
4. 决策树算法
这里举一个简单的例子,来说明决策树算法的过程。现在假设某公司要发布某种产品,在发布产品前,先进行了用户调查,获得如下信息:
| 性别(A) | 年龄(B) | 婚姻状况(C) | 是否购买(Y) |
|---|---|---|---|
| M | 小 | 未婚 | Yes |
| F | 中 | 已婚 | No |
| F | 小 | 未婚 | Yes |
| M | 大 | 已婚 | No |
| M | 中 | 离异 | No |
| M | 中 | 未婚 | Yes |
| F | 大 | 已婚 | No |
| M | 大 | 未婚 | Yes |
| F | 大 | 未婚 | No |
| F | 中 | 已婚 | No |
假设我们的训练样本就是以上10条记录,每条记录有四个字段,前三个字段是用户属性,其中性别属性有两个值,M(男)和F(女),为了方便,这里把年龄属性离散化为三个值,即小、中和大,婚姻状况属性也有三个值;第四个字段为是否购买产品,其中购买的有4条记录,不购买的有6条记录。
现在我们将是否购买(目标变量Y)分别按性别(A)、年龄(B)和婚姻(C)三个属性进行划分。比如,性别为M的记录有5条,其中有3条是购买记录,2条是不购买记录,性别为F的记录也有5条,其中有1条购买记录,4条不购买记录,如下图所示:
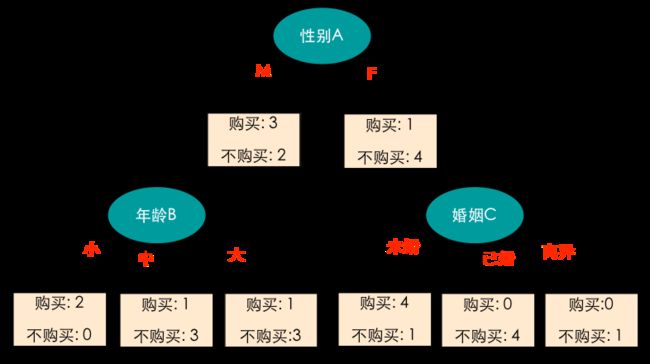
这里就有一个问题,我们应该先选择哪个属性进行划分呢?我们知道,训练样本有10条记录,分为两类,一类是购买的,有4条记录,另一类是不购买的,有6条记录,因此在划分前的类分布是(0.4, 0.6)。如果使用性别属性来划分,则子女结点的类分布分别为(0.6, 0.4)和(0.2, 0.8),此时子女结点仍然包含两个类的记录;如果按照婚姻属性进行划分,将得到纯度更高的划分,子女结点的类分布分别为(0.8, 0.2)、(0, 1)和(0, 1),也就是说,当我们选择婚姻这个属性进行划分的时候,类分布不平衡的程度比较高,或者说纯度比较高,这样的好处就在于我们划分的次数会比较少。
比如,如果我们先按照婚姻属性进行划分,可以发现已婚和离异的记录不用再进行划分了,因为他们都是属于不购买的人群,所以就只剩下未婚的记录了,这时只有5条记录,我们再从性别和年龄中选择一个属性,得到一个纯度更高的划分,如此进行下去,不难发现,这正是一种贪心的属性选择策略。
这时问题就来了,我们用什么指标来刻画每次划分的类分布不平衡程度呢?根据指标的不同,就会产生以下几种算法,ID3、C4.5和CART等。
4.1 ID3算法
Q: ID3算法以什么作为属性选择的度量?
A: ID3算法以[信息增益]作为属性选择的度量,选择分裂后[信息增益最大的属性]进行分裂。
下面定义几个概念,说明什么是信息增益,其中信息熵(entropy)、信息增益(gain)和期望信息等均是从信息论中引申出来的概念。
-
熵(entropy)
设样本数据为S,类别变量为Y,则样本数据S的类别变量Y的信息熵表示为:
Entropy(S)=−∑i=1cpilog2(pi)
其中c是类别的个数, pi 表示第 i 个类别在整个训练记录中出现的概率,可以用属于此类别的记录数除以训练记录总数作为估计。在计算熵时, 0log20=0 。
比如,对上面的训练样本,可以得到类别变量Y的信息熵为:
Entropy(S)=−0.4log20.4−0.6log20.6=0.97 -
期望信息
设将样本数据S按照属性X进行划分,且属性X有k个值 x1,x2,⋯,xk ,则X对S划分的期望信息为:Entropy(S|X)=∑j=1k|Sj||S|⋅Entropy(Sj)
其中, Sj 为当属性 X 取值 xj 时的样本数据, |Sj| 为样本数据 Sj 的大小, |S| 为样本数据 S 的大小,Entropy( Sj )是样本数据 Sj 的目标变量 Y 的信息熵。比如,对上面的训练样本,我们用性别属性A对训练样本进行划分,产生两个小样本,由上面的划分图可以看到,此时左结点有5条记录(小样本大小为5),右结点也有5条记录(小样本大小为5),因此可以得到A对S划分的期望信息为:
Entropy(S|A)=510×[−3/5×log2(3/5)−2/5×log2(2/5)]+510×[−1/5×log2(1/5)−4/5×log2(4/5)]=0.846
如果我们用婚姻属性C对训练样本进行划分,则会产生三个小样本,由上面的划分图可知,三个小样本大小分别为5,4,1,因此得到C对S划分的期望信息:
Entropy(S|C)=510×[−4/5×log2(4/5)−1/5×log2(1/5)]+410×[−0/4×log2(0/4)−4/4×log2(4/4)]+110×[−0/1×log2(0/1)−1/1×log2(1/1)]=0.361
同理,可计算出B对S划分的期望信息为0.649。 -
信息增益
设将样本数据S按照属性X进行划分,则属性X的信息增益为:
Gain(X)=Entropy(S)−Entropy(S|X)
ID3算法在每次需要分裂时,计算每个属性的信息增益,然后从中挑选出信息增益最大的属性作为分裂结点。比如,对于上面的训练样本,我们分别计算性别A、年龄B和婚姻C的信息增益:
⎧⎩⎨⎪⎪Gain(A)Gain(B)Gain(C)=Entropy(S)−Entropy(S|A)=0.97−0.846=0.124=Entropy(S)−Entropy(S|B)=0.97−0.649=0.321=Entropy(S)−Entropy(S|C)=0.97−0.361=0.609由此可以看到,婚姻属性的信息增益最大,因此,我们首先选取婚姻属性进行分裂,对于分裂后的样本再从中选取信息增益最大的属性进行分裂,如此进行下去。
4.2 C4.5算法
ID3算法选择信息增益作为分裂指标,但存在一个问题,它偏向于取值较多的属性作为分裂节点,针对这一问题,C4.5算法引入增益比率(gain ratio)作为分裂指标。
首先,C4.5定义了属性X的分裂信息(splitInfo),它是样本数据S中属性X的信息熵:
其中各符号意义与ID3算法相同。
接着,定义增益比率为:
Q: C4.5算法如何分裂?
A: C4.5算法在每次需要分裂时,选择具有最大[增益比率]的属性作为分裂属性。Q: 在C4.5算法中,何时停止分裂?
A: C4.5算法停止分裂的条件主要有:
- 一个结点的所有目标变量样本值均为同一类别;
- 若无属性可用于划分当前样本集,则将当前结点强制划为叶结点,并把样本数目最多的类别标记为预测类别;
- 如果分裂后剩余的样本数小于某个给定的阈值,则返回一个叶结点,并把众数类别标记为预测类别。例如取值为10,如果剩余样本数小于10,则自动归为叶结点,停止分裂。这实际上是一种前剪枝的方式。
4.3 CART算法
CART的全称为Classification And Regression Tree,即分类回归树。它既可以对分类型目标变量建模,也可以对连续型目标变量建模(回归分析)。
与ID3,C4.5算法类似,CART算法也使用目标变量的纯度来分裂决策节点,只是它使用的是Gini增益。需要注意的是,CART算法只支持二叉树。
假设样本数据为S,输入自变量(即属性)为 Xj ,目标变量为 Y 。在分裂前,样本数据S的目标变量 Y 的Gini增益被定义为:
其中,c表示类别个数, pi 表示第 i 个类别在整个训练样本中出现的概率。
设样本数据S按照属性 X 进行划分,且属性 X 有k个值 x1,x2,⋯,xk ,则在属性 X 下,样本数据S的目标变量 Y 的Gini增益被定义为:
其中, Sj 为当属性 X 取值 xj 时的样本数据, |Sj| 为样本数据 Sj 的大小, |S| 为样本数据 S 的大小,Gini( Sj )是样本数据 Sj 的目标变量 Y 的Gini增益。
则属性 X 的Gini增益被定义为:
Q: CART算法如何分裂?
A: CART算法在每次需要分裂时,计算每个属性的[Gini增益],然后选择Gini增益最大的属性进行分裂。Q: CART何时停止分裂?
A: CART算法停止分裂的条件主要有:
- 决策树最大深度(maxdepth):如果决策树的层数已经达到了制定的深度,则停止生长;
- 最小样本分裂数(minsplit):如果结点包含的样本数已低于最小样本数minsplit,则不再分裂;
- 树中叶结点所包含的最小样本数(minbucket):如果自变量X分裂后生成的叶结点所包含的样本数低于最小样本数minbucket,则此次分裂无效,自变量X不再进行分裂;
与ID3算法使用的信息增益一样,Gini增益作为分裂指标也具有[偏向于选择取值较多的属性作为分裂结点]的缺点,针对这一问题,C4.5算法引入增益率(gain ration)作为分裂指标解决这个问题,而CART算法使用Gini增益,通过限制只能进行二分支分裂来解决(这也是CART算法只能做二分支决策树的主要原因)。
4.4 决策树分类的特点
- 决策树分类是一种构建分类模型的非参数方法。换句话说,它不要求任何先验假设,不假定类和其他属性服从一定的概率分布;
- 找到最佳的决策树是NP完全问题。许多决策树算法都采取启发式的方法指导对假设空间的搜索。前面介绍的算法就采用了一种贪心的、自顶向下的递归划分策略建立决策树;
- 决策树相对容易解释,特别是小型的决策树。在很多简单的数据集上,决策树的准确率可以与其他分类算法相媲美;
5. 参考资料
- 张洋,http://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html
- 数据挖掘导论,Pang-Ning Tan 等著,范明 等译
- R语言与网站分析,李明 著