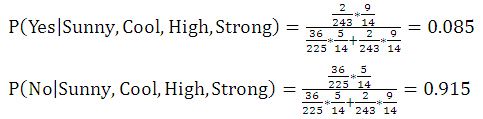【机器学习】机器学习(四、五、六):线性分类、高斯判别分析(GDA)、朴素贝叶斯(NB)
简介:
这篇文章主要介绍简单的二分类算法:线性分类器、高斯判别分析、朴素贝叶斯。
一、线性分类器
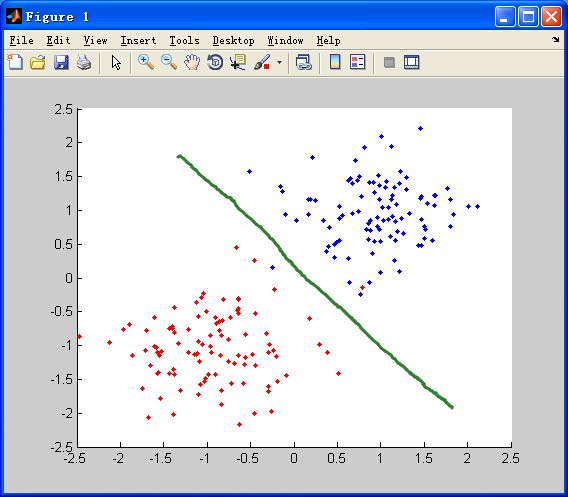
加入给定如下两类数据(0-1),目测分类器应该对这组数据进行这样的划分。图中,红色样本点表示0,蓝色样本点表示1。
原始数据显示为三维如下:
现在运用前一节介绍的线性拟合来进行分类,即线性分类器。当拟合出来的y值大于等于0.5,则归为1,;否则归为0。
代码如下:
%%
%线性分类器
function Classification_Liner
%%
clc;
clear all;
close all;
%%
n=3;%特征数
m=200;%样本数
x=zeros(m,n);
v0=randn(m/2,2)*0.5-1;
v1=randn(m/2,2)*0.5+1;
figure;hold on;
%axis([-5 5 -5 5]);
plot(v0(:,1),v0(:,2),'r.');
plot(v1(:,1),v1(:,2),'b.');
x(:,1)=1;
x(:,2)=[v0(:,1);v1(:,1)];%前100组是一类,后100组是另一类
x(:,3)=[v0(:,2);v1(:,2)];
y=[zeros(m/2,1);ones(m/2,1)];%前100组是一类,后100组是另一类
%%
figure;hold on;
plot3(x(1:m/2,2),x(1:m/2,3),y(1:m/2,1),'r.');
plot3(x(m/2+1:m,2),x(m/2+1:m,3),y(m/2+1:m,1),'b.');
%%
theta=((x'*x)\x')*y;%最小二乘法
y=x*theta;
for i=1:m
if (y(i,1)>=0.5)
y(i,1)=1;
else
y(i,1)=0;
end
end
figure;hold on;
plot3(x(1:m/2,2),x(1:m/2,3),y(1:m/2,1),'r.');
plot3(x(m/2+1:m,2),x(m/2+1:m,3),y(m/2+1:m,1),'b.');
for i=1:n
fprintf('theta%d=%f;\n',i-1,theta(i,1));%打印估计的参数
end
%完
输出结果:
二、高斯判别分析法(GDA)
简单的来说,以一维高斯为例,有两个不同的正态分布如下,当测试点为x1时,可知概率:g0(x1)>g1(x1),此时x1会被判为服从g0(x)的分布,即判别为g0(x)类。当测试点为x2时,显然会判别为g1(x)类。这种也会存在判别失误的情形,例如,x2点本来属于g0(x),但是会判别为g1(x)类。同理可知二维或高维的正态分布情形。
具有n维特征的0-1情况,当然前提是0-1类是服从高斯多元正态分布的。
多元正态分布的公式:
当输入一个测试样本点x时,计算是落在0类的概率大还是落在1类的概率大,将x归于概率较大的那一类。
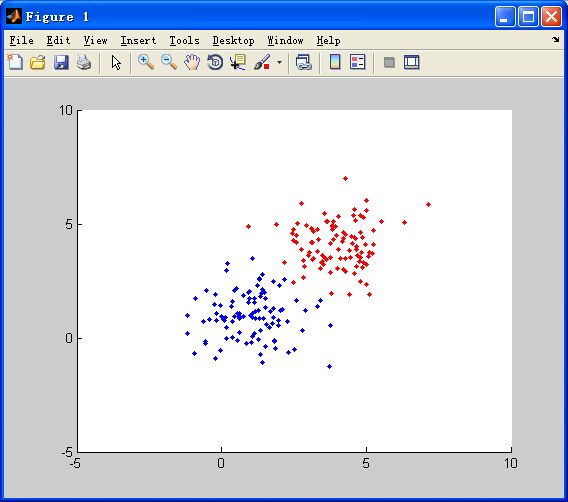
当输入为如下数据时(2维特征的),0类样本点标记为红色,1类标记为蓝色。
其三维视图为:
对上述样本点运用进行高斯判别分析法(GDA)分类,代码如下:
%%
%高斯判别分析法
clc;
clear all;
close all;
%%
m=200;
n=2;
rp=mvnrnd([1 1],[1 0;0 1],m/2);%生成正样本1
rn=mvnrnd([4 4],[1 0;0 1],m/2);%生成负样本0
y=[ones(m/2,1);zeros(m/2,1)];
figure;hold on;
plot3(rp(:,1),rp(:,2),y(1:m/2,1),'b.');
plot3(rn(:,1),rn(:,2),y(m/2+1:m,1),'r.');
axis([-5 10 -5 10]);
hold off;
x=[rp;rn];
p=sum(y)/m;
%%
positive=find(y);%找到正样本1位置
negative=find(y==0);
%%
mu1=mean(x(positive,:));%计算正(1)样本点均值
mu2=mean(x(negative,:));%计算负(0)样本点均值
sigma1=cov(x(positive,:));%计算样本点协方差矩阵
sigma2=cov(x(negative,:));%计算样本点协方差矩阵
sigma_1=sigma1^(-1);
sigma_2=sigma2^(-1);
A1=1/(((2*pi)^(n/2))*((det(sigma_1))^(1/2)));
A2=1/(((2*pi)^(n/2))*((det(sigma_2))^(1/2)));
for i=1:m
p0=A1*exp((-1/2)*(x(i,:)-mu1)*sigma_1*(x(i,:)-mu1)');%落在某类的概率
p1=A2*exp((-1/2)*(x(i,:)-mu2)*sigma_2*(x(i,:)-mu2)');
if (p0>p1)
y(i,1)=1;
else
y(i,1)=0;
end
end
%%
figure;hold on;
plot3(x(positive,1),x(positive,2),y(positive,1),'b.');
plot3(x(negative,1),x(negative,2),y(negative,1),'r.');
axis([-5 10 -5 10]);
hold off;
%完
输出结果为,明显有一个点判别错误:
如果要看详细的数学推导公式的话,请自行查阅STANFIRD机器学习公开课的讲义。
三、朴素贝叶斯(NB)
在介绍朴素贝叶斯之前,先要介绍一下条件概率、全概率、贝叶斯的知识,阮一峰讲得较为通俗易懂【五:水糖果问题】:http://www.ruanyifeng.com/blog/2011/08/bayesian_inference_part_one.html
网上看到个形象的举例,我在这里也用它,是根据天气情况来判断是否适合打羽毛球。
根据上表数据,14个样本中,有5个No和9个Yes,则可计算先验概率:P(Yes)=9/14,P(No)=5/14。类条件概率为:P(Xi|Yes)和P(Xi|No),其中Xi=(Outlook,Temperature,Humidity,Wind)。
当输入一个新的样本时,算出其后验概率大小。例:输入新样本X=(Sunny,Cool,High,Strong),现在判断这样的天气是否时候打球。
则:
显然,可以判别输入样本的天气情况不适合打球。