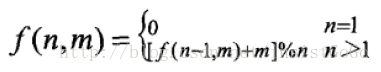每日一题(60) - 圆圈中最后剩下的数字

题目来自剑指Offer

题目：

思路（1）：

朴素算法，每走m步，删除一个数。游标越界重回起点。

复杂度：O(m*n)，n为环中数字，m为走的步数。

分析，每走m步删除一个数，则删除n-1个数，需要（n-1）*m步，即为O(m*n)。

代码：借助STL的list类

#include <iostream>
#include <assert.h>
#include <list>
using namespace std;
int LastNum(int n,int m)
{
	assert(n > 0 && m > 0);
	list<int> circle;
	for (int i = 0;i < n;i++)
	{
		circle.push_back(i);
	}
	int nCount = 1;
	list<int>::iterator iterTmp;
	list<int>::iterator iter = circle.begin();
	while(circle.size() != 1)
	{
		if (nCount == m)
		{
			iterTmp = iter++;//注意迭代器失效的问题
			circle.erase(iterTmp);
			nCount = 1;
		}
		else
		{
			nCount++;
			iter++;
		}
		if (iter == circle.end())
		{
			iter = circle.begin();
		}
	}
	
	return *(circle.begin());
}
int main()
{
	cout<<LastNum(5,3)<<endl;//3
	cout<<LastNum(1,10)<<endl;//0
	cout<<LastNum(8,5)<<endl;//2
	cout<<LastNum(6,6)<<endl;//3
	system("pause");
	return 1;
}

思路（2），借助书中的思想，很巧妙。

思想：每删除一个数，都做一次转换，把剩余的数转换为删之前的形式，再次进行删除，使得时间复杂度降为O（n）。

思路：

这里假设，给出n个数字（0到n-1），每次删除第m个数字，其中用f（n，m）表示剩余的最后哪一个数字。

删除之前的序列：0,1,2,3,...,k-1,k,k+1,...,n。

假设本次删除的数字为k,其中k = （m-1）%n，则删除后的序列为：0,1,2,3,...,k-1,k+1,...,n。

注意，为什么k = （m-1）%n？这是因为n可能比m小。比如，n=3（0到2），m=5。第一次删除的数为1。

此时，我们对删除k后的数字进行处理：

假设转换前的数字为x，转换后的数字为y，则可得y = (x - k - 1 + n) % n。之后继续对转换后的数字进行删除。

如果知道y，我们也可以找到其对应的 x 值，其x = （y + k + 1）% n。

注：可以不用求反函数得到两个公式：

（1）转换前的数x 比 转换后的数y 多了k+1，之后直接相减，但相减后可能为负数，所以要加上n，之后在取余。

（2）转换后的数y 比 转换前的数x 少了k+1，之后直接相加取余即可。

给出两个假设。

（1）对转换前的n-1个数继续删除，最后剩下的数字为x = f'(n-1,m)。由于该序列数不是从0开始的，不能写成f(n-1,m)的形式。

（2）继续对转换后的n-1个数进行删除，最后剩余的数字为y = f(n-1,m)。

根据假设（1）可知，一定有f（n，m） = f'（n-1，m）成立。

我们继续对转换之前和转换之后的序列进行删除，最终得到的数一个为x，一个为y。

注意，此x和y一定是对应的。虽然转换前后两个序列中的数不同，但是对于最终留下的哪一个数，它们所在的下标应该是一样的。

即，一定有f'（n-1，m） =（ f（n-1，m） + k + 1）%n。

此时，相当于已知y（等于 f（n-1，m）），而要求解x，且x对应着f'（n-1，m）。

根据上述思想，可得：

f（n，m） = f'（n-1,m）= ( f（n-1，m） + k + 1）%n。

而k = （m - 1）%n成立，带入上式子可得，

则有f（n，m） =（ f（n-1，m） +m）%n。

即， 我们 对n-1个数（0到n-2）进行删减最终得到的数 稍做处理 ，即可得到对n个数（0到n-1）进行删减最终得到数。

给出递归式：

此时，我们给出递归式直观含义：转换之后的数 y 相当于将转换之前的数 x 在大小上减少了m，所以在对转换之后的数求解f（n-1，m）后，该数也相当于少了m，此时要加上m，即为f（n，m）。但是要注意的是，加上m后可能会超过n，所以还有对n取余。

说明：为啥说转换之后的数相当于将转换之前的数在大小上减少了m？

这是因为删除一个数之前的序列为：0到n-1，

删除m-1之后且转换之前的序列为：m，m+1，...，n-1,0，...m-2。

删除m-1之后且转换之后的序列为：0,1，...

经过对比，转换前后序列相差是为m，求出最终的数也应该相差m。

-------------------------------------

举例：假设n = 4（0-3），m = 3，求解最终剩下的数（为0）

（1）f(4,3) = [ f(3,3) + 3 ] %4 

（2）f(3,3) = [ f(2,3) + 3 ] %3 

（3）f(2,3) = [ f(1,3) + 3 ] %2 

（4）f(1,3) = 0：只有一个数（0），直接返回。

（5）f(2,3) = 1，f(3,3) = 1，f(4,3) = 0

注意：式子是对此时待删除序列的长度进行取余。

代码：

#include <iostream>
#include <assert.h>
#include <list>
using namespace std;
int LastNum(int n,int m)
{
	int nLen = 2;//从两个数才是算
	int nLastNum = 0;//只有一个数的时候，剩下为0
	while(nLen <= n)
	{
		nLastNum = (nLastNum + m) % nLen;
		nLen++;
	}
	return nLastNum;//返回的即是最后一个数，也是其下标
}

int main()
{
	cout<<LastNum(5,3)<<endl;// 3
	cout<<LastNum(1,10)<<endl;//  0
	cout<<LastNum(8,5)<<endl;//  2
	cout<<LastNum(6,6)<<endl;// 3
	cout<<LastNum(2,3)<<endl;//  1
	cout<<LastNum(3,3)<<endl;//  1
	system("pause");
	return 1;
}

注意：我们在推导递归式时，什么x啊y啊，都是指的数组下标，递归式中返回值也为下标。而最终剩下的那个数与下标相同也仅仅是因为我们删减前的数和其下标一样，都是0到n-1。

如果我们待处理的数字不是0到n-1，甚至是一些不连续的，该递归式也是可以处理的。

此时我们可以直接返回下标对应的哪一个数即可。

#include <iostream>
#include <assert.h>
#include <list>
using namespace std;
int LastNum(int nArr[8],int n,int m)
{
	int i = 2;//从两个数才是算
	int nLastNum = 0;//只有一个数的时候，剩下为0
	while(i <= n)
	{
		nLastNum = (nLastNum + m) % i;
		i++;
	}
	assert(nLastNum >= 0 && nLastNum < n);
	return nArr[nLastNum];//返回的即是最后一个数，也是其下标
}

int main()
{
// 	int nArr[5] = {1,2,3,4,5};
// 	cout<<LastNum(nArr,5,3)<<endl;//4
	
// 	int nArr[8] = {1,2,3,4,5,6,7,8};
// 	cout<<LastNum(nArr,8,3)<<endl;//7
	
 	int nArr[6] = {2,5,7,12,18,20};
 	cout<<LastNum(nArr,6,3)<<endl;//2

	system("pause");
	return 1;
}

当然，使用链表的思路也是可以处理该情况的，仅仅改变插入list中的数即可，这里代码不表了。