POJ 1160 dp + 四边形优化

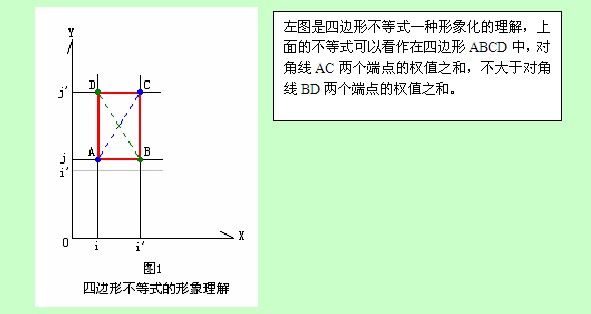
一、四边形不等式基本理论

在动态规划的转移方程中，常见这样一种转移方程：

这两个定理证明在赵爽的《动态规划加速原理之四边形不等式》中给出了相关的证明。

【题意】给出m个村庄及其距离，给出n个邮局，要求怎么建n个邮局使代价最小.

【分析】

dp(i,j)=min(dp(i-1,k)+w(k+1,j)) , i-1<=k<j  s(i-1,j)<=k<=s(i,j+1)

w(i,j)=w(i,j-1)+val[j]-val[(j+i)/2] , i<j<=n

dp(1,i)=w(1,i), w(i,i)=0, s(1,i)=0

对于函数w(i,j)有人可能疑问，从i到j建一座邮局，对于邮局位置k,(i<=k<=j)，这是一个凹区间，k选在i ,j的中间位置w(i,j)才是最小的，如何j-i是一个奇数，那么中间的两个数都是距离最小的点。对于w满足四边形不等式和区间单调性（本人表示不大会证，一般动态转移方程类似，n^3不能解决的问题，都是这么搞吧）。于是，我们限制了原方程中k的取值范围，得到了O(n^2)算法。

【AC代码】

#include <iostream>
#include <cstdio>
using namespace std;
#define inf 0x7ffffff
#define MIN(a,b) ((a)<(b)?(a):(b))
int dp[31][301];
int val[301];
int w[301][301];
int s[31][301];//表示前i-1个邮局的城市数

int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=1; i<=n; ++i)
        {
            scanf("%d",&val[i]);
        }
        for(int i=1; i<=n; ++i)
        {
            w[i][i]=0;
            for(int j=i+1; j<=n; ++j)
            {
                w[i][j]=w[i][j-1]+val[j]-val[(i+j)/2];
            }
        }
        //init1.
        for(int i=1; i<=n; ++i)
        {
            for(int j=1; j<=m; ++j)
            {
                dp[j][i]=inf;
            }
        }
        //init2.
        for(int i=1; i<=n; ++i)
        {
            dp[1][i]=w[1][i];
            s[1][i]=0;
        }
        //dp.
        for(int i=2; i<=m; ++i)
        {
            s[i][n+1]=n;//s[i][j]定义为使得dp(i,j)对应的决策的最大值
            for(int j=n; j>i; --j)
            {
                for(int k=s[i-1][j]; k<=s[i][j+1]; ++k)//四边形优化
                {
                    if(dp[i-1][k]+w[k+1][j]<dp[i][j])
                    {
                        s[i][j]=k;
                    }
                    dp[i][j]=MIN(dp[i][j],dp[i-1][k]+w[k+1][j]);
                }
            }
        }
        printf("%d\n",dp[m][n]);
    }
    return 0;
}