hdu 5148 树形dp，分组背包

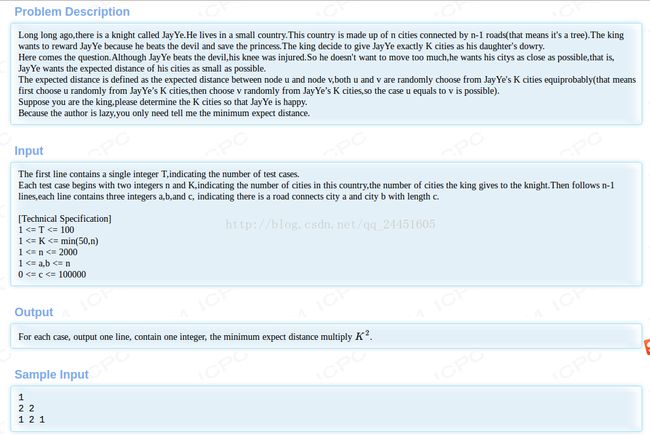
题目：

题目分析：

状态方程： dp[当前节点的标号][当前已经选取的城市数]

设已经选取的城市数是K

初始状态： dp[u][0] = dp[u][1] = 0 ， 其他的将值设置为无穷大

树形转移： dp[father][k] = min ( dp[father][k] , dp[father][k1] + dp[son][k-k1] + k1 *( k-k1)*weight_of_edge );

讲解： 给出的点组成了一个树形结构，而且是求取最优解，所以我们可以运用动态规划，方程存的值是当前状态下最小的子情况，我们可以利用分组背包进行状态转移，把每个子树看做一组物品，每组物品中只有已经选取的城市数不同，每件物品的花费是当前路径在规划中的总花费，这条边下面子树选取了k1个点，这条边另一侧要选取k-k1个点，所以一定有且仅有k1*(k-k1)t条路径经过这条边，所以花费可得

代码如下，不懂可以在评论中提问，当天回复

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAX 4007

using namespace std;

struct 
{
    int v,next,w;
}e[MAX];

int t,k,n;
int head[MAX];
long long dp[MAX][57];
int cc;

void add ( int u , int v , int w  )
{
    e[cc].v = v;
    e[cc].w = w;
    e[cc].next = head[u];
    head[u] = cc++;
}

void dfs ( int u , int fa )
{
    dp[u][0] = 0;
    dp[u][1] = 0;
    for ( int i = head[u] ; i != -1 ; i = e[i].next )
    {
        int v = e[i].v;
        if ( v == fa ) continue;
        dfs ( v , u );
        for ( int j = k ; j >= 0 ; j-- )
        {
            for ( int t = 1 ; t <= j ; t++ )
                dp[u][j] = min ( dp[u][j] , dp[u][j-t] + (long long) dp[v][t] + (long long)(t*(k-t)* e[i].w ) );
        }
    }
}

int main ( )
{
    int a ,b , c ;
    scanf ( "%d" , &t );
    while ( t-- )
    {
        scanf ( "%d%d" , &n , &k );
        memset ( head , -1 , sizeof ( head ) );
        cc = 0;
        for ( int i = 1 ; i < n ; i++ )
        {
            scanf ( "%d%d%d" , &a , &b , &c  );
            add ( a , b ,c );
            add ( b , a ,c ); 
        }
        memset ( dp , 0x3f , sizeof ( dp ) );
        dfs ( 1 , -1 );
        printf ( "%lld\n" , dp[1][k]*2  );
    }
}