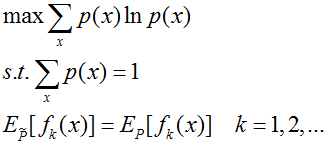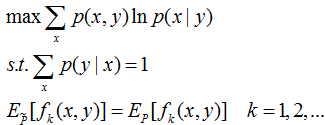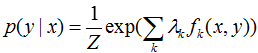最大熵模型

最大熵模型一直困惑了我很久，直到最近看了exponential family才明白。最大熵解的形式属于exponential family。

第一部分

首先考虑一个问题：给定一些样本，求估计p(x)的分布。

根据最大熵模型，这个问题可以写成最优化问题：

其中为经验分布，表示样本中X=x出现的概率。

下面给出最大熵的大白话定义：

为了估计随机变量p(x)的分布，在给定限制条件下，我们总是选择熵最大的分布。上式的第2,3条就是限制条件。其中第3条的意思是：fk(x)为任意函数，fk(x)关于经验分布的期望与fk(x)关于未知分布P(x)的期望相同。其中fk(x)可以自己选取。（原文：fk(x) is an arbitrary function, the moments of the distribution match the empirical moments of fk(x). 【1】chap. 9.2.6）

求解此最优化问题，得到解：

其中Z为归一化因子。过程在此略过，用拉格朗日法，见【1】 chap. 9.2.6。

其中仍为未知量，需要通过IIS、拟牛顿法等方法迭代解出。

给个例子：给一些样本，试求其分布f(x)

（1）当我们没有给定fk(x)时，解得f(x)=1/N，为均匀分布。

（2）当我们给定f1(x)=x^2，f2(x)=x时，可以得到解的形式

是正态分布。

第二部分

最大熵模型在词性标注中很有用，推导选自【2】，另给出一篇词性标注论文【3】

即给定单词x，求其词性为y的概率。即求P(y|x)，因此我们发现最大熵模型是判决模型

和上文相似，求解条件熵最大值转为最优化问题：

第1式为条件熵最大化，第3式为经验分布应与未知分布期望相同。

解之得

其中Z为归一化因子。

在词性标注中f(x,y)作为特征函数，常如下选取：

选择很多特征函数之后，便可以用最大熵模型进行词性判别了。

开发工具

网上常用张乐开发的maxent工具包。

【1】 Kevin P. Murphy, "Machine Learning A Probabilistic Perspective"

【2】 李航 《统计学习方法》

【3】 李泽中等. "基于最大熵模型结合CRFs的中文词性标注"

博主e-mail：[email protected]