poj2406—KMP next数组的性质求最小周期

题目大意：给出一个字符串，求它最多有几个连续子串构成

分析：KMP求最小周期——结论：如果一个字符串有最小周期，那么最小周期为n-next[n]

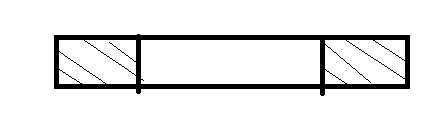
考虑整个串，根据next数组的定义，前后匹配并且前缀和相等的最长的后缀之间没有交叉，那么相等的部分的长度为next[n]，并且从左往右相等。

如果希望中间的也是有s[1..next[n]]的几个循环组成，那么整个串就以next[n]为最小周期，但是如果这样，next[n]就会变大，与现在的情况矛盾。

那么n % (n-next[n])!=0，整个串为一个循环节，只有一个周期

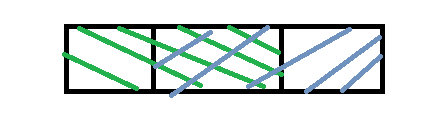
①如果前缀和后缀是有重叠的，如图，那么蓝色和绿色相交的地方的第一个字母等于绿色的第一个字母……那么中间至少有一个以s[1..n-next[n]]为循环节的字符串。

证明：假设有这样的例子ABAB……AB使得前缀后缀有重叠并且中间重叠部分不是由那种循环节组成，比如ABABCAB ，ABABACAB，那么将后缀往前平移的时候不能与前缀重合。所以这种情况中间一定是循环节，并且和两边相等。

②如果单独的蓝色和绿色部分不相等而中间有重合，比如A.........C=>AA......CC显然矛盾

这时n % (n-next[n])==0，并且循环节为n-next[n]

周期的个数为n / (n-next[n])

另外所有可能的周期长度为 n-next[n],n-next[next[n]],n-next[next[next[n]]]...

因为如果后面已经匹配了，相当于再在前next[x]个数中找一个相同的循环节，最小循环节*2 *3 *4之类的。。。如果再能被整除的话就是一个新的周期了

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
using namespace std;
int next[1000010];
int n,t;
char s[1000010];

void getnext()
{
    int j=-1;
    next[0]=-1;
    for (int i=1;i<n;i++)
    {
        while (j>-1 && s[j+1]!=s[i]) j=next[j];
        if (s[j+1]==s[i]) j++;
        next[i]=j;
    }
}
int main()
{
    scanf("%s", s);
    while (s[0]!='.')
    {
        n=strlen(s);
        getnext();
        t=next[n-1]+1;
        if (n % (n-t)==0) printf("%d\n", n / (n-t)); else printf("%d\n", 1);
        scanf("%s", s);
    }
}