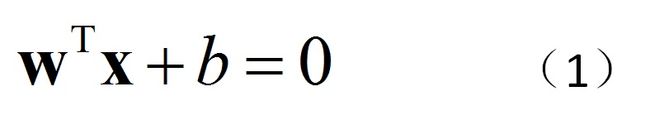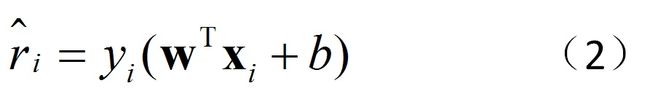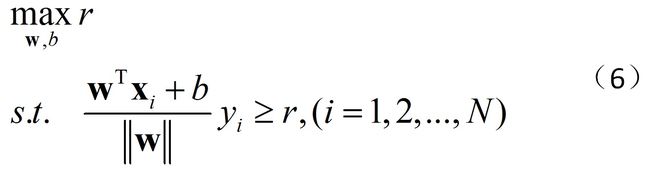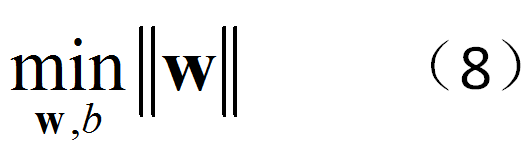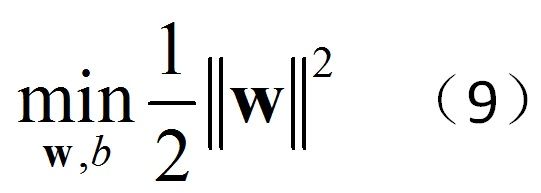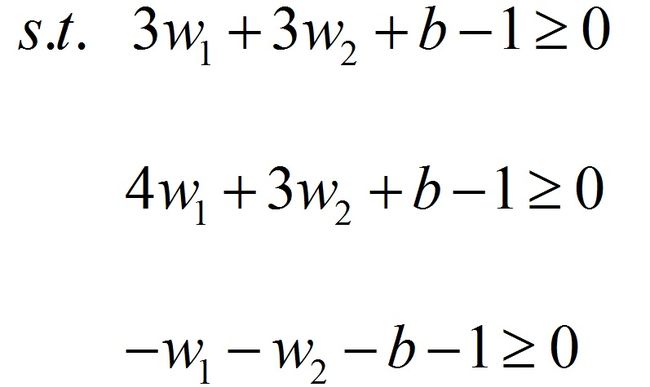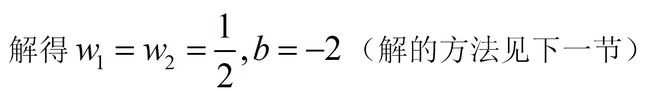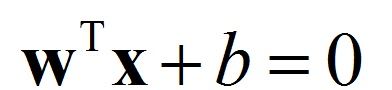支持向量机（一）

本篇是学习SVM的初学讲义，希望能够对大家有所帮助。SVM涉及到很多拉格朗日对偶等最优化知识，强烈推荐大家学习《最优化计算方法》，不然理解SVM会遇到很多困难。学习之前强烈推荐先玩一玩林智仁的svm-toy.exe，对理解SVM很有帮助，链接在

http://download.csdn.net/detail/richard2357/5382093

 

好了，接下来我们开始SVM的学习。在本文中，会尽量避免一些数学公式，本文只是为初学者理清脉络，详尽的数学推导可以在任一本机器学习教材中找到。

 

SVM是用来分类的算法。可以分类的算法还有决策树、贝叶斯、人工神经网络等。为什么SVM现在这么火？笔者总结了一些优缺点如下：

 

优点：

1.人工神经网络是黑箱算法，而支持向量机有严格的理论支持，有严格的误差上下界。

2.模型法（如人工神经网）需要大量样本训练，而SVM可以在小样本时表现很好。

3.只有少数支持向量决定了最终结果，剔除了冗余点，增删非支持向量对模型没有影响，具有鲁棒性。

4.通过核方法将线性不可分数据映射到高维空间，在高维空间线性可分，可以解决非线性问题。

 

不足：

1.训练样本规模很大时难以实施。

2.解决多分类问题存在困难。

 

直观认识:

首先我们来一点儿直观的认识，最基本的SVM，就是寻找一个区分两个不同类别的最优超平面的算法。

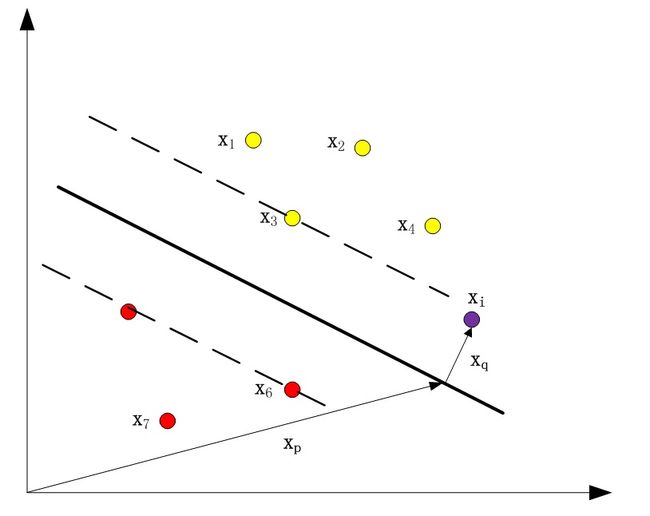
                                                 图1

 

图1中x₃,x₅,x₆是“支持向量”，“机”表示一种算法。在SVM分类时，只有“支持向量”是起作用的。增删非支持向量对模型没有影响。

 

训练数据集T：

T共有N个元素，每个元素形式为（特征，目标值）

T = { (x₁, y₁), (x₂, y₂), ..., (x_N, y_N) }

其中x_i ∈ Rⁿ, y_i∈{+1, -1}, i = 1, 2, ..., N

在图1中我们不妨把黄色类的点标记为+1，红色类的点标记为-1

则图中训练集为

T = { (x₁, +1), (x₂, +1), (x₃, +1), (x₄, +1), (x₅, -1), (x₆, -1), (x₇, -1) }

为方便起见，拿图1来说，图中有N个点。平面的方程为：

 

函数间隔：

对于图中的任意一个元素(x_i,y_i)，其中y_i∈{+1, -1}，定义其到平面的函数间隔为

 

其中乘以y_i能保证一定非负。

如图1，对于紫色的点，将x_i =x_p +x_q代入（2），并利用（1），可将（2）化简为

我们发现，对于同样的分割平面（1），w的方向是确定的，但大小可变，导致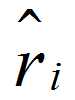随着w变化而变化。因此我们引入几何间隔。

 

几何间隔：

对于图中的任意一个元素(x_i, y_i)，其中y_i∈{+1, -1}，定义其到平面的几何间隔为

与函数间隔相比，只是除了一个，由高数知识可知，这是点到到面的距离。可化简为

其中乘以y_i能保证r_i一定非负。

图中每个点x_i对应一个r_i，为了让决策平面最恰当地把两类分开，我们记（即距平面最近的点到平面的距离），很直观，我们需要做的就是要（即让所有点都离决策平面远一点）。这就是支持向量机最朴素的思想。

因此寻找超平面转化为最优化问题：

我们可以把这个最优化问题稍稍变形一下，使其更好解。我们知道决策平面只与w的方向有关，而与w的大小无关。上述不等式变形为

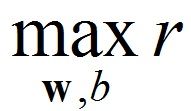由于的大小对分割平面(1)没有影响。因此我们可以调整的大小使，则等价于

（8）等价于

最优化问题6变为

用（9）代替（8）的原因是转化成二次规划问题，导数连续，比绝对值方便的多，最优化教材中专门有一节讲二次规划的解法。是为

了求导后计算方便。解这个最优化问题便可得到决策平面（1）。

 

例题：

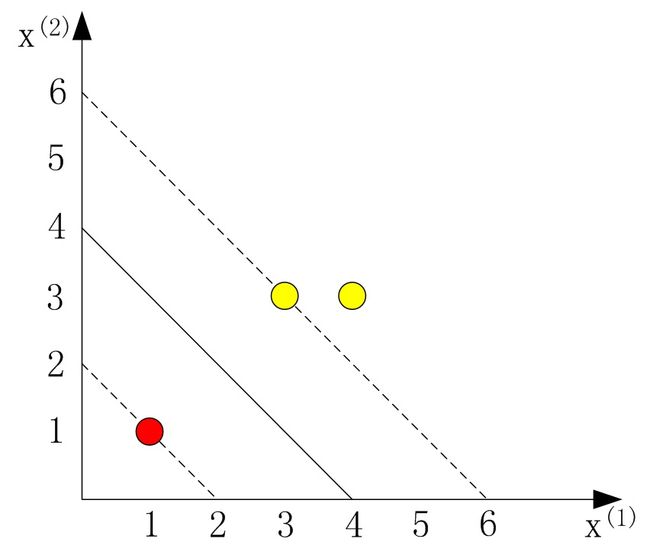
正例点x₁ = (3, 3),x₂ = (4, 3)，反例点x₃ = (1, 1)，求最大间隔分离超平面。（摘自李航《统计学习方法》p103）

                                     图2

解：由公式（10），等价于解最优化问题：解得

  

最大间隔分离超平面为

 

       至此，一个简单的支持向量机就已经介绍完毕了。那为什么要引入“对偶”算法呢？具体内容将在下一节中进行讨论。

博主e-mail：[email protected]