树链剖分 学习指南

什么是树链剖分

树链剖分并不是一个复杂的算法或者数据结构，它能把一棵树拆成链。

树链，就是树上的路径。剖分，就是把路径分类为重链和轻链。

给定一棵树，将它划分成若干条互不相交的路径，满足：从节点 u->v 最多经过 logn 条路径以及 logn 条不在路径上的边。

树链剖分后，我们就可以利用其它的数据结构对在一棵树上进行路径的修改、求极值、求和的一类问题进行求解了。

一些定义

重儿子：以结点的一个儿子为根的子树的结点个数中最大的那一个儿子称为重儿子。

轻儿子：除了重儿子以外的儿子。

重边：结点与其重儿子的边称为重边。

轻边：结点与其轻儿子的边称为轻边。

重链：由重边组成的路径。

轻链：由轻边组成的路径。

描述剖分后的树

描述结点:

siz[v]：以结点v为根的子树的结点个数

dep[v]：结点v的深度，定义根结点的深度为0

fa[v]：结点v的父亲结点

描述结点与路径之间的关系:

belong[v]：结点v所属的路径编号

idx[v]：结点v在其路径中的编号

son[v]：结点v的重儿子

描述路径：

top[p]：编号为p的路径的顶端结点

len[p]：路径p的长度

描述辅助数据结构：

sump[p]：路径p的编号

seg[v]：结点v的父边在线段树中的位置

wei[v]：结点v的父边的权值

剖分后的性质

如果 (u,v) 为轻边，则 siz[v] * 2 < siz[u]，即以轻儿子为根的子树中的结点数量相对少。

从根到某一点的路径上轻链、重链的个数都不大于 logn。

树链剖分的实现

首先用一次搜索求出 dep、fa、wei 的值，深搜广搜都可以，但是深搜容易爆栈，这里使用广搜。

在广搜的过程中得到了树的拓扑序，我们按照拓扑序的逆序遍历所有的结点。

在这个过程中可以求出 siz 与 son。

对于一个结点，如果它是叶子结点，那么我们就新建一条链，使该结点作为链上的第一个结点；

如果不是叶子结点，那么它与它的重儿子属于同一条链，对链进行更新即可。

void split(){
    memset(dep,-1,sizeof(dep));
    l=0;
    dep[ que[r=1]=1 ]=0; // 将根结点插入队列，并设深度为0
    fa[1]=-1; // 默认 1 为根结点
    wei[1]=0;
    while (l<r){ // 第一遍搜索求出 fa,dep,wei
        int u=que[++l];
        vis[u]=false; // 顺便初始化vis
        for (int i=head[u];i!=-1;i=edges[i].next){
            int v=edges[i].to;
            int w=edges[i].w;
            if (dep[v]==-1){ // 未访问过的结点
                dep[ que[++r]=v ]=dep[u]+1; // 将v插入队列并设深度为dep[u]+1
                fa[v]=u; // v的父结点为u
                wei[v]=w; // v的父边权值
            }
        }
    }
    cnt=0; // 重链编号
    for (int i=n;i>0;i--){
        int u=que[i],p=-1;
        siz[u]=1;
        son[u]=p;
        for (int k=head[u];k!=-1;k=edges[k].next){
            int v=edges[k].to;
            if (vis[v]){ // 若v是u的子结点
                siz[u]+=siz[v]; // 计数
                if (p==-1||siz[v]>siz[p]){
                    son[u]=v;
                    p=v; // u的重儿子是v
                }
            }
        }
        if (p==-1){ // u是叶子结点
            idx[u]=len[++cnt]=1; // 一个新的路径编号为cnt，u是路径中的第一个结点
            belong[ top[cnt]=u ]=cnt; // u是顶端结点，且u属于路径cnt
        }
        else{ // u不是叶子结点
            idx[u]=++len[ belong[u]=belong[p] ]; // u属于重儿子所在的链，链长+1，u是路径中第len个结点
            top[ belong[u] ]=u; // u是顶端结点
        }
        vis[u]=true; // 访问标记
    }
}

路径上的求和、求极值操作

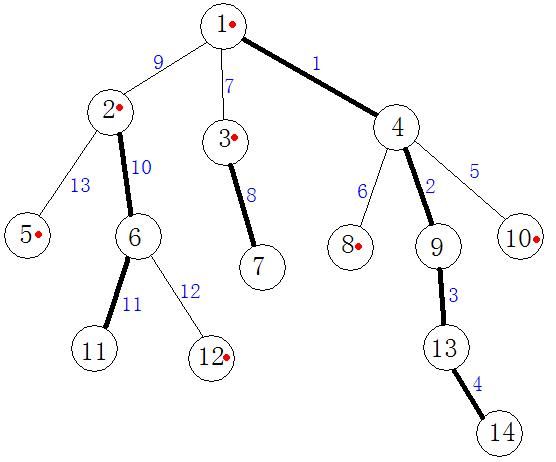
我们对树上的边进行编号，编号对应着该边在线段树上的位置，保证同一个重链上的所有点的父边的编号是连续的即可。

这样我们就可以通过对线段树进行区间操作来快速的修改同一条重链上的权值了。

如图所示：

如何快速的处理任意两个结点 (va,vb) 间的边呢。

我们设 f1=top[belong[va]]，f2=top[belong[vb]]。表示 f1 是 va 所属的链上的最顶端的点， f2 是 vb 所属的链上的最顶端的点。

当 f1 != f2 时，若 dep[f1] >= dep[f2]，那么就处理 va 的父边到 f1 父边的路径，由于它们属于同一条重链的父边，编号是连续的，因此可以用线段树进行区间处理，最后使 va = fa[f1]，重复进行该步骤直到 f1=f2。

当 f1 = f2 时，va 与 vb 在同一条重链上，若 va 与 vb 不是同一点，就区间处理 va 到 vb 路径上的边，否则修改完成。

查询操作与修改操作是类似的。

例如要查找两个结点间路径上的权值最大的边：

int find(int va,int vb){
    int f1=top[belong[va]],f2=top[belong[vb]],tmp=0;
    while (f1!=f2){
        if (dep[f1]<dep[f2]){
            swap(f1,f2);
            swap(va,vb);
        }
        tmp=max(tmp,tr.query(1,seg[f1],seg[va]));
        va=fa[f1];
        f1=top[belong[va]];
    }
    if (va==vb) return tmp;
    if (dep[va]>dep[vb]) swap(va,vb);
    return max(tmp,tr.query(1,seg[son[va]],seg[vb]));
}

相关练习题

SPOJ 375. Query on a tree

题目给出一棵含有n个结点的树，n-1条边每条边都有边权，有两种操作，修改第i条边的边权，查询两个结点的路径上最大的边权。

首先进行树链剖分，对边进行编号，建立线段树储存权值。

对于修改操作，我们找到该边在线段树上的位置然后单点更新即可。

对于查询操作，利用重链上的父边编号相同这一性质不断进行区间查询，就能快速找到最大的边权。

POJ 3237 Tree

与上一题相比多了一种操作，将两个结点间的边权取负。

用线段树维护两个值，区间上的最小值与最大值。区间取负时将最大值最小值取负后交换，打上延迟标记。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int maxn=101010+5;
const int maxm=maxn+maxn;

struct EDGENODE{
    int to;
    int w;
    int next;
}edges[maxm];
int head[maxn],edge;
inline void init(){
    edge=0;
    memset(head,-1,sizeof(head));
}
inline void addedge(int u,int v,int w){
    edges[edge].w=w,edges[edge].to=v,edges[edge].next=head[u],head[u]=edge++;
    edges[edge].w=w,edges[edge].to=u,edges[edge].next=head[v],head[v]=edge++;
}
int que[maxn]; // 队列
bool vis[maxn]; // 访问标记
int son[maxn]; // 重儿子
int idx[maxn]; // 结点v在其路径中的编号
int dep[maxn]; // 结点v的深度
int siz[maxn]; // 以结点v为根的子树的结点个数
int belong[maxn]; // 结点v所属的路径编号
int fa[maxn]; // 结点v的父亲结点
int top[maxn]; // 编号为p的路径的顶端结点
int len[maxn]; // 路径p的长度
int sump[maxn]; // 路径p的编号
int seg[maxn]; // 结点v的父边在线段树中的位置
int wei[maxn]; // 结点v的父边的权值
int l,r,ans,cnt;
int n;
char cmd[22];

void split(){
    memset(dep,-1,sizeof(dep));
    l=0;
    dep[ que[r=1]=1 ]=0; // 将根结点插入队列，并设深度为0
    fa[1]=-1; // 默认 1 为根结点
    wei[1]=0;
    while (l<r){ // 第一遍搜索求出 fa,dep,wei
        int u=que[++l];
        vis[u]=false; // 顺便初始化vis
        for (int i=head[u];i!=-1;i=edges[i].next){
            int v=edges[i].to;
            int w=edges[i].w;
            if (dep[v]==-1){ // 未访问过的结点
                dep[ que[++r]=v ]=dep[u]+1; // 将v插入队列并设深度为dep[u]+1
                fa[v]=u; // v的父结点为u
                wei[v]=w; // v的父边权值
            }
        }
    }
    cnt=0; // 重链编号
    for (int i=n;i>0;i--){
        int u=que[i],p=-1;
        siz[u]=1;
        son[u]=p;
        for (int k=head[u];k!=-1;k=edges[k].next){
            int v=edges[k].to;
            if (vis[v]){ // 若v是u的子结点
                siz[u]+=siz[v]; // 计数
                if (p==-1||siz[v]>siz[p]){
                    son[u]=v;
                    p=v; // u的重儿子是v
                }
            }
        }
        if (p==-1){ // u是叶子结点
            idx[u]=len[++cnt]=1; // 一个新的路径编号为cnt，u是路径中的第一个结点
            belong[ top[cnt]=u ]=cnt; // u是顶端结点，且u属于路径cnt
        }
        else{ // u不是叶子结点
            idx[u]=++len[ belong[u]=belong[p] ]; // u属于重儿子所在的链，链长+1，u是路径中第len个结点
            top[ belong[u] ]=u; // u是顶端结点
        }
        vis[u]=true; // 访问标记
    }
}
const int INF=0x3fffffff;
struct SegmentTree{
    int num[maxn];
    struct Tree{
        int l;
        int r;
        int max;
        int min;
        bool neg;
    };
    Tree tree[maxn*4];
    void push_down(int root){
        if (tree[root].neg){
            if (tree[root].l!=tree[root].r){
                tree[root<<1].neg^=1;
                tree[root<<1|1].neg^=1;
                swap(tree[root<<1].max,tree[root<<1].min);
                swap(tree[root<<1|1].max,tree[root<<1|1].min);
                tree[root<<1].max*=-1;
                tree[root<<1].min*=-1;
                tree[root<<1|1].max*=-1;
                tree[root<<1|1].min*=-1;
            }
        }
        tree[root].neg=0;
    }
    void push_up(int root){
        tree[root].max=max(tree[root<<1].max,tree[root<<1|1].max);
        tree[root].min=min(tree[root<<1].min,tree[root<<1|1].min);
    }
    void build(int root,int l,int r){
        tree[root].l=l;
        tree[root].r=r;
        tree[root].neg=0;
        if(tree[root].l==tree[root].r){
            tree[root].max=num[l];
            tree[root].min=num[l];
            tree[root].neg=0;
            return;
        }
        int mid=(l+r)/2;
        build(root<<1,l,mid);
        build(root<<1|1,mid+1,r);
        push_up(root);
    }
    void update(int root,int pos,int val){
        if(tree[root].l==tree[root].r){
            tree[root].max=val;
            tree[root].min=val;
            return;
        }
        push_down(root);
        int mid=(tree[root].l+tree[root].r)/2;
        if(pos<=mid) update(root<<1,pos,val);
        else update(root<<1|1,pos,val);
        push_up(root);
    }
    int query(int root,int L,int R){
        if(L<=tree[root].l&&R>=tree[root].r) return tree[root].max;
        push_down(root);
        int mid=(tree[root].l+tree[root].r)/2,ret=-INF;
        if(L<=mid) ret=max(ret,query(root<<1,L,R));
        if(R>mid) ret=max(ret,query(root<<1|1,L,R));
        push_up(root);
        return ret;
    }
    void nega(int root,int L,int R){
        if (L<=tree[root].l&&R>=tree[root].r){
            tree[root].neg^=1;
            swap(tree[root].max,tree[root].min);
            tree[root].max*=-1;
            tree[root].min*=-1;
            return;
        }
        push_down(root);
        int mid=(tree[root].l+tree[root].r)/2;
        if (L<=mid) nega(root<<1,L,R);
        if (R>mid) nega(root<<1|1,L,R);
        push_up(root);
    }
    void debug(int root){
        printf("rt=%d, [%d~%d], min=%d, max=%d, neg=%d\n",root,tree[root].l,tree[root].r,tree[root].min,tree[root].max,(int)tree[root].neg);
        if (tree[root].l==tree[root].r) return;
        debug(root<<1);
        debug(root<<1|1);
    }
}tr;

int find(int va,int vb){
    int f1=top[belong[va]],f2=top[belong[vb]],tmp=-INF;
    while (f1!=f2){
        if (dep[f1]<dep[f2]){
            swap(f1,f2);
            swap(va,vb);
        }
        tmp=max(tmp,tr.query(1,seg[f1],seg[va]));
        va=fa[f1];
        f1=top[belong[va]];
    }
    if (va==vb) return tmp;
    if (dep[va]>dep[vb]) swap(va,vb);
    return max(tmp,tr.query(1,seg[son[va]],seg[vb]));
}
void gao(int va,int vb){
    int f1=top[belong[va]],f2=top[belong[vb]];
    while (f1!=f2){
        if (dep[f1]<dep[f2]){
            swap(f1,f2);
            swap(va,vb);
        }
        tr.nega(1,seg[f1],seg[va]);
        va=fa[f1];
        f1=top[belong[va]];
    }
    if (va==vb) return;
    if (dep[va]>dep[vb]) swap(va,vb);
    tr.nega(1,seg[son[va]],seg[vb]);
}
int d[maxn][3];

int main()
{
    int T;
    scanf("%d",&T);
    while (T--){
        init();
        scanf("%d",&n);
        for (int i=1;i<n;i++){
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            d[i][0]=a;
            d[i][1]=b;
            d[i][2]=c;
            addedge(a,b,c);
        }
        split();
        sump[0]=0;
        for (int i=1;i<=cnt;i++) sump[i]=sump[i-1]+len[i];
        for (int i=1;i<=n;i++){
            seg[i]=sump[ belong[i] ]-idx[i]+1;
            tr.num[ seg[i] ]=wei[i];
        }
        tr.build(1,1,n);
        while (scanf("%s",cmd)){
            if (cmd[0]=='D') break;
            int x,y;
            scanf("%d%d",&x,&y);
            if (cmd[0]=='Q'){
                printf("%d\n",find(x,y));
            }
            if (cmd[0]=='C'){
                if (fa[d[x][1]]==d[x][0]) tr.update(1,seg[d[x][1]],y);
                else tr.update(1,seg[d[x][0]],y);
            }
            if (cmd[0]=='N'){
                gao(x,y);
            }
        }
    }
    return 0;
}

/**
1
10
1 2 1
2 3 3
3 4 8
4 5 -6
5 6 -9
6 7 -1
7 8 1
8 9 7
9 10 6
NEGATE 1 8
CHANGE 2 7
QUERY 1 3
NEGATE 1 5
CHANGE 4 7
QUERY 3 5
DONE

3
10
1 2 1
2 3 7
3 4 8
4 5 6
5 6 9
6 7 1
7 8 1
8 9 7
9 10 6
NEGATE 4 7
CHANGE 2 3
QUERY 2 9
CHANGE 2 3
QUERY 6 8
NEGATE 1 8
CHANGE 2 7
QUERY 1 3
NEGATE 1 5
CHANGE 4 7
QUERY 3 5
DONE
6
1 2 1
2 3 2
3 4 4
4 5 100
5 6 -1000
QUERY 1 2
CHANGE 1 3
QUERY 1 2
NEGATE 1 2
QUERY 1 3
QUERY 1 2
CHANGE 1 10
QUERY 1 3
NEGATE 1 2
QUERY 1 3
CHANGE 1 10
CHANGE 2 20
QUERY 1 3
NEGATE 1 2
QUERY 1 3
NEGATE 2 3
QUERY 1 3
CHANGE 1 -100
CHANGE 2 -1000
QUERY 1 4
NEGATE 1 6
QUERY 1 6
DONE
100
1 2 265
2 3 133
3 4 508
4 5 197
5 6 437
6 7 849
7 8 577
8 9 503
9 10 478
10 11 434
11 12 877
12 13 691
13 14 54
14 15 295
15 16 421
16 17 166
17 18 550
18 19 410
19 20 868
20 21 476
21 22 283
22 23 410
23 24 915
24 25 308
25 26 301
26 27 553
27 28 609
28 29 733
29 30 770
30 31 635
31 32 581
32 33 753
33 34 707
34 35 448
35 36 738
36 37 841
37 38 389
38 39 532
39 40 210
40 41 458
41 42 595
42 43 989
43 44 678
44 45 214
45 46 746
46 47 548
47 48 117
48 49 758
49 50 437
50 51 840
51 52 555
52 53 726
53 54 490
54 55 719
55 56 403
56 57 329
57 58 92
58 59 311
59 60 664
60 61 207
61 62 170
62 63 548
63 64 713
64 65 556
65 66 705
66 67 82
67 68 508
68 69 59
69 70 45
70 71 670
71 72 540
72 73 826
73 74 262
74 75 504
75 76 989
76 77 408
77 78 896
78 79 388
79 80 15
80 81 485
81 82 219
82 83 977
83 84 641
84 85 985
85 86 189
86 87 64
87 88 641
88 89 320
89 90 788
90 91 441
91 92 785
92 93 163
93 94 153
94 95 852
95 96 36
96 97 10
97 98 145
98 99 956
99 100 641
QUERY 32 69
NEGATE 1 22
CHANGE 40 53
QUERY 17 38
NEGATE 17 65
CHANGE 49 68
QUERY 44 52
NEGATE 11 53
CHANGE 9 68
QUERY 2 49
NEGATE 25 45
CHANGE 23 67
QUERY 89 90
NEGATE 5 37
CHANGE 27 53
QUERY 22 86
NEGATE 6 7
CHANGE 17 23
QUERY 78 93
NEGATE 30 63
CHANGE 56 99
QUERY 3 29
NEGATE 24 38
CHANGE 9 95
QUERY 63 66
NEGATE 69 92
CHANGE 9 91
QUERY 7 27
NEGATE 32 60
CHANGE 48 77
QUERY 47 94
NEGATE 14 27
CHANGE 50 99
QUERY 38 97
NEGATE 11 67
CHANGE 74 83
QUERY 28 81
NEGATE 13 53
CHANGE 55 88
QUERY 2 66
NEGATE 71 95
CHANGE 32 74
QUERY 14 50
NEGATE 1 28
CHANGE 16 80
QUERY 36 75
NEGATE 20 49
CHANGE 22 54
QUERY 5 46
NEGATE 12 37
CHANGE 61 94
QUERY 18 92
NEGATE 19 26
CHANGE 6 94
QUERY 33 60
NEGATE 79 87
CHANGE 30 75
QUERY 55 94
NEGATE 28 79
CHANGE 23 31
QUERY 91 95
NEGATE 28 76
CHANGE 8 41
QUERY 6 25
NEGATE 19 70
CHANGE 17 54
QUERY 52 66
NEGATE 4 95
CHANGE 19 52
QUERY 73 87
DONE


**/