矩阵快速幂小结
矩阵快速幂大概是用来解决这样一类问题,当你知道了一个递推式比如a[n]=a[n-1]+a[n-2] 题目要求你求出a[n]。如果n大于1亿怎么办?
不可能用for。解决办法就是根据递推式构造一个矩阵A,最终会化简为a[n]=A^n类似的形式,再利用快速幂,快速的求出A^n,所以原先的
O(n)就变成了O(logn)
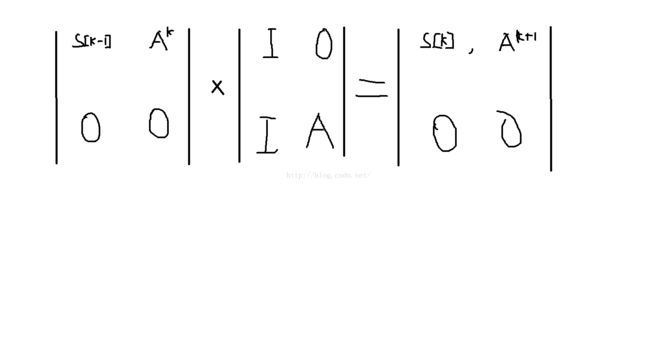
例如POJ 3233 递推关系是 s[k]=s[k-1]+A^k;
所以s[K]=( | 1 0| ^n )*s[1]
| 1 A|
下面给出矩阵快速幂的模板
矩阵连乘:
struct Node
{
int a[25][25];
};
int n,m,x,y,k,t;
Node multiply(Node a,Node b)
{
Node c;
memset(c.a,0,sizeof(c.a));
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(!a.a[i][j]) continue;
//减枝,有些题目写减枝才可以过,n有些大的时候。有的题目n有500,n^3就会炸了,这类题目,要观察矩阵的形式,可以把矩阵转
换的,用n^2就可以完成连乘,例如POJ 3150 后面的例题里有
for(int k=0;k<n;k++)
{
(c.a[i][k]+=(a.a[i][j]*b.a[j][k])%mod)%=mod;
}
}
}
return c;
}
矩阵快速幂:
Node quick(Node a,int x)
{
Node c;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
c.a[i][j]=(i==j?1:0);
for(x;x>0;x>>=1)
{
if(x&1)
c=multiply(c,a);
a=multiply(a,a);
}
return c;
}练习题目:
http://poj.org/problem?id=3233
题解:
http://blog.csdn.net/dacc123/article/details/51204052
http://poj.org/problem?id=3735
题解:
http://blog.csdn.net/Dacc123/article/details/51204080
http://poj.org/problem?id=3150
题解:
http://blog.csdn.net/dacc123/article/details/51222518
http://acm.hdu.edu.cn/showproblem.php?pid=2604
题解:
http://blog.csdn.net/dacc123/article/details/51207863
http://acm.hdu.edu.cn/showproblem.php?pid=2157
题解:
http://blog.csdn.net/dacc123/article/details/51205684
http://acm.hdu.edu.cn/showproblem.php?pid=1575
题解:
http://blog.csdn.net/dacc123/article/details/51205878
http://poj.org/problem?id=3070
题解:
http://blog.csdn.net/dacc123/article/details/51222489