PRML笔记之INTRODUCTION
一、引子
机器学习与传统的计算机算法区别就在一个“学习”上——让计算机程序脱离程序员的预设,通过自己学习来解决问题。
本章从手写数字识别(属于监督学习的范畴)的例子开始,引出诸多贯穿全书的概念和符号。
怎么使用机器学习的方法来解决手写数字识别的问题?通俗地说,就是要求你设计一个机器人(开始的时候的机器人还很sb)。然后你手写一个数字,比如说0,教机器人说:“这玩意儿是0。”;然后你又写了一个3,再教机器人这是3;然后你又写,又教;又写,又教……重复N遍之后,你再手写一个数字,机器人自己就能认出它是几,这时候机器人就会觉得你很sb了。
从你觉得机器人sb到机器人觉得你sb的过程涵括了以下两个概念:
trainning set:就是你那些手书,对应课本上的就是数字图片集合。形式化表示为![]() ,其中每个x代表一个图片向量。
,其中每个x代表一个图片向量。
target vector:就是你教机器人的东西,对应课本上就是数字图片对应的数字。
generalization:我们的最终目的就是让机器人认识新的手写数字,但是我们获得的训练数据往往是有限的,比如上例中,训练数据只有你自己的笔迹,这就要求我们设计的机器人具有泛化能力,也就是使用有限的数据训练机器人后,机器人能识别其他人包括你自己的手书。
下面书中提到了监督学习、费监督学习、强化学习等概念。较为简单。
二、多项式回归问题
2.1多项式回归问题的非概率解释
数据:synthetically generated data
->为什么要使用synthetically generated data?
我们认为现实生活中的数据隐藏着潜在的规律,但具体来说每个数据个体又会受到随机噪声的干扰。而书中synthetically generated data可以很好的模拟现实数据的这种状态。
方法:多项式曲线拟合(Polynomial Curve Fitting)
使用多项式来拟合数据,并使用一个error function来训练多项式中的参数。但这样会出现过拟合问题,所以后面加入了regularization term来减轻这个问题。这里有几个疑问,为什么要用那样一个error function?为什么加入regularization term就会减轻过拟合问题?这就要用到概率论和贝叶斯理论来解释。
2.2多项式回归问题的概率解释
最大似然方法:
最大似然的思想是,求一个参数,使观测到的数据出现的概率最大。假设给定一个新的x,它对应的t是由拟合函数y(x,w)加上一个高斯噪声得到的,即 t=y(x,w)+e。那么t的分布则为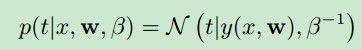 ,因为数据时独立同分布的,所以就可以用最大似然函数法求解参数w。这样得到的结果与前面使用error function 的方法是一致的,即最大似然就是前面error function的概率解释。这种方法存在过拟问题,课本上用了抛硬币的例子做了直观解释。
,因为数据时独立同分布的,所以就可以用最大似然函数法求解参数w。这样得到的结果与前面使用error function 的方法是一致的,即最大似然就是前面error function的概率解释。这种方法存在过拟问题,课本上用了抛硬币的例子做了直观解释。
MAP:
由于最大似然法存在过拟合问题,所以我们想到用“更贝叶斯(more Bayesian)”的方法来求解w。这里我们对参数w有一个先验知识,就像抛硬币问题,我们预先知道,正反面出现的概率大约都是0.5,,而这里某个w出现的概率是p(w),称为w的先验分布。有了先验就可以获得w的后验,让w的后验最大,可求出w的解。这样得到的结果与前文中加入regularization term的结果是一致的。但这还不是完全的贝叶斯方法,因为此处w仍旧是一个参数,也就是说模型仍旧是固定的(即多项式中x的阶或者说w的个数是固定的)。
贝叶斯方法:
无论是最大似然还是MAP都是获得w的一个点估计,而我们最终的目的是得到预测值t的分布即p(t|x,x,t),此处预测值t依赖于新输入的x以及我们已有的观测值x和其对应的t。而此分布可以用加法和乘法公式获得,即p(t|x,x,t) = ∫ p(t|x,w)p(w|x,t)dw。然后我们可以使用evidence approximation方法求解其中的超参数(hyperparameter),具体方法在第三章会讲到。贝叶斯方法的优点就是在训练超参数的过程中,会自动选择模型。
三、决策阶段
上面我们求出了诸多概率,这些概率有什么用呢?对于新的x,我们对于其对应的t取值有不确定性,所以在推理阶段我们使用概率来表示这个不确定性,然后在决策阶段使用这个概率来进行最优决策。
下面提到了解决决策问题的三个模型——生成模型(generative models)、判别模型(discriminative models)、判别函数(discriminative function),判别函数很容易理解。前两种模型的区别网上有一些解释——What is the difference between a Generative and Discriminative Algorithm?
其他问题
M的选择?
不同的M即不同的模型(model),怎样选择最优的M即最优的模型,这涉及到本书一个重要的概念——model selection or model comparison。我们期望模型可以在训练中自动选择,这要用到本书最精髓的理论——贝叶斯理论,此理论将于第三章和第四章详细讲述。
p(D|w)在频率论与贝叶斯理论中的不同?
频率论中,w是一个参数,意即其值是固定的,但我们不知道,就像一个方程中的x,我们通过最大化 p(D|w)的方法来求得w的值。
贝叶斯理论中,w是一个变量,意即w可取任意值,但我们会对每个可能的w的值给出一个概率,来表示我们对w取这个值的不确定性是多少。
这个问题初学时较难理解,学习完第三、四章时基本可以理解,学习过程中可以参考《模式识别》相关内容。
贝叶斯理论应用问题?
由于贝叶斯方法通常需要在整个参数域做积分,所以有时候是难以计算的。但Markov chain Monte Carlo、variational Bayes、expectation propagation等方法打开了进入贝叶斯实战领域的大门。