treap学习小结（一）

Q:什么是treap?

A:treap=tree+heap

其实，简单来说，treap就是把BST（二叉查找树）和heap结合了起来。

通过heap（堆）来维护BST的平衡，保证每次操作的复杂度是O(logn)级别的。

Q:那么如何通过heap来维护BST的平衡呢？

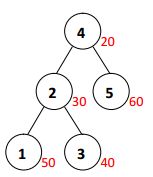
A:在图片中黑色的数字表示权值，他是满足BST性质的（即左儿子小于父亲，右儿子大于父亲）。

红色的数据是通过随机函数生成的一个fix值（修正值），他是满足小根堆性质的（父亲小于所有儿子）。

Q:为什么heap可以维护BST的平衡呢？

A:每次往树中插入一个结点时，如果他的权值是递增（或递减）的，BST就会退化成一条链，操作时间复杂度变成O(n)。

但是如果每次在插入一个结点时，随机生成一个fix值，如果他小于父亲的fix值，就把他旋到父亲位置（旋转之后仍然满足BST性质），那么画一下图就可以知道，树就不是一条链了，他会变得平衡起来~

因为fix是随机生成的，因此在实践中有很好的效果。

接下来说一下treap的基本操作。

（一）旋转

在旋转之后树一定还满足BST的性质，怎么旋转呢？

和splay的zigzag原理是完全一样的，可以看这里。

但是有非常重要的区别是：treap中zigzag的x是指需要被旋转的点的父亲，而splay中就是指需要被旋转的节点本身。

void Push_up(int x)   
{
	a[x].size=a[a[x].l].size+a[a[x].r].size+1;
}
void zag(int &x)   //这里一定要用引用
{
	int t=a[x].l;
	a[x].l=a[t].r;
	a[t].r=x;
	a[t].size=a[x].size;
	Push_up(x);
	x=t;
}
void zig(int &x)
{
	int t=a[x].r;
	a[x].r=a[t].l;
	a[t].l=x;
	a[t].size=a[x].size;
	Push_up(x);
	x=t;
}

（二）插入

和普通的BST一样，先找到插入的位置，然后建立新的结点，但是与BST不同的是建立新的结点时要随机生成一个修正值，为了保证小根堆的性质，对其进行适当旋转。

如图，要插入权值为4的结点，找到位置后生成新的结点，同时随机生成了了一个修正值为15.但是他比父亲的修正值（30）要小，为了满足小根堆的性质，我们要把以3为根的子树左旋。

但是旋转之后仍然不满足小根堆的性质（15比父亲的20要小），所以进行一次右旋。

现在，整棵树满足小根堆的性质，同时在旋转过程中这棵树一直都是满足BST的性质的。

void New_node(int &x,int data)
{
	x=++tot;
	a[x].data=data;
	a[x].l=a[x].r=0;
	a[x].fix=rand();  //随机生成修正值
	a[x].size=1;
}
void Insert(int &x,int data,int no)
{
	if (!x)   //找到位置了，插入新结点
	{
		New_node(x,data,no);
		return;
	}
	a[x].size++;
	if (data<=a[x].data)
	{
		Insert(a[x].l,data,no);
		if (a[a[x].l].fix<a[x].fix) zag(x);
	}
	else
	{
		Insert(a[x].r,data,no);
		if (a[a[x].r].fix<a[x].fix) zig(x);
	}
}

（三）删除

首先当然要找到删除结点所在的位置，和插入时找结点的方法是基本一样的。

删除要考虑两种情况：

1.没有或有一个儿子:

把结点值赋值为a[x].l+a[x].r（为什么呢？因为没有儿子值就是0~所以直接相加就行了~）

2.有两个儿子

通过旋转，使他变成可以直接删除的结点

void Delet(int &x,int data)
{
	if (a[x].data==data)   //找到被删除结点所在的位置了
	{
		if (a[x].l*a[x].r==0) x=a[x].l+a[x].r;  //第一种情况
		else if (a[a[x].l].fix<a[a[x].r].fix)   //第二种情况
		{
			zag(x);
			Delet(x,data);
		}			
		else
		{
			zig(x);
			Delet(x,data);
		}
	}
	else if (a[x].data>data)
	{
		a[x].size--;
		Delet(a[x].l,data);
	}
	else
	{
		a[x].size--;
		Delet(a[x].r,data);
	}
}

（四）查找第k大

方法是通过每个结点的size递归寻找即可，分三种情况：

（1）当前的结点x就是第k个数，直接返回当前结点的值

（2）第k个数在左子树中，递归寻找左子树中第k大的值

（3）第k个数在右子树中，递归寻找右子树中第(k-1-a[a[x].l].size大的值)

int findkth(int x,int k)
{
	if (k==a[a[x].l].size+1) return a[x].data;  //第一种情况
	if (k<=a[a[x].l].size) return findkth(a[x].l,k);  //第二种情况
	else return findkth(a[x].r,k-1-a[a[x].l].size);   //第三种情况
}

如果对本文有疑问或者有修改意见的欢迎在文章下面发表评论~

参考：

byvoid 《随机平衡二叉查找树treap的分析与应用》