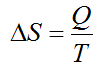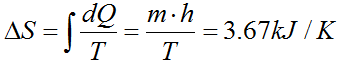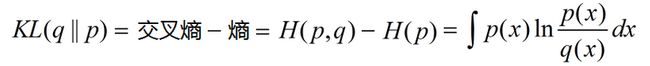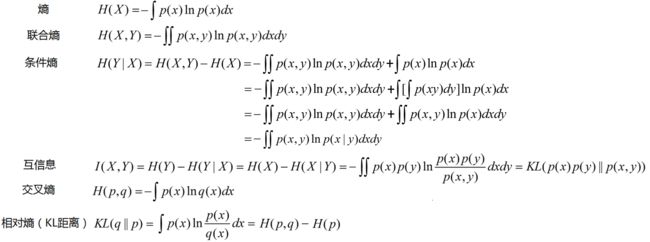熵
最近为了学习最大熵模型,整理了一些熵的资料,深入理解了一下熵。
0.引言。香农熵的定义:
![]()
这个式子大家应该都熟悉。但为什么要这样定义?为什么会有一个log出现?下面我们来一步步揭开疑惑。
1.1854年克劳修斯提出熵的热力学定义。【1】
注意这条公式只涉及到熵的增减。给个大物上的例题可以加深理解:
例:已知T=273K下,1kg冰融化成水的溶解热为h=334KJ/kg,试求3kg冰融化成水时的熵变。
解:
2.1877年波尔兹曼提出熵的统计学定义。 【1】【2】
![]()
其中k为波尔兹曼常数,Ω为状态数。比如有三个骰子,那么状态数就为6^3。波尔兹曼熵有以下三点特征:
(1)对于一个宏观态就有一个Ω与之对应,熵是一个态函数(克劳修斯熵只涉及熵的增减)
(2)熵的意义是分子热运动的无序性的一种量度。
(3)熵具有可加性。S=S1+S2。
其中的第三点解释了为什么要用log。考虑含有两个子系统的整体。系统一有3个骰子,系统二有4个骰子。那么S1 = ln(6^3),S2 = ln(6^4)。对于整体有S = ln(6^7)。我们可以惊喜地发现S=S1+S2。log的作用是把乘法变成了加法。我想这也是波尔兹曼引入log的原因。
3.1948年香农将熵引入信息论。 【3】
这个公式相比大家都非常熟悉。但它从何而来,为何如此定义?我想香农首先考虑了一个这样的问题:
问题:假设一共有N个球,扔到k个桶中。但这些桶大小是不同的。假设扔到第i个桶里的概率是pi,即第i个桶里有ni个球,那么一共有多少种不同分法(状态数)?【4】
解:香农算得状态数
接下来他查阅了一下文献,发现了波尔兹曼熵,于是借用过来:
![]()
把W带入,令N趋于无穷,就得到了(详细推导见【4】)
![]()
!!!!这样这个公式终于露出了庐山真面目!!
补充:
(1)求和号同样可以变成积分。
(2)当对数底为2时熵的单位是bit,底为e时熵的单位是nat,底为10时熵的单位是dit。【1】
4.三种熵的关系
文献【5】给出了这三种熵的关系(说实在我也没太看懂)
![]()
5.联合熵
![]()
当且仅当X, Y在统计学上相互独立时等号成立。
6.交叉熵
考虑如下的概率分布,试求发送信息所需的最小编码长度
| p(x1) | p(x2) | p(x3) | p(x4) | |
| 概率 | 0.5 | 0.25 | 0.125 | 0.125 |
如上表格概率分布实际的需要的编码长度为0.5*1+0.25*2+0.125*3+0.125*3=1.75(即熵),假如错误地估计q(x)为q(x1)=q(x2)=q(x3)=q(x4)=0.25,每个事件使用两位二进制
那么实际的编码长度为0.5*2+0.25*2+0.125*2+0.125*2=2,这个值记作交叉熵,写作:
7.KL距离(相对熵)
由于错误使用q(x)估计p(x)产生的信息增量
8.常用的熵一览表
本文有些观点可能有误或不完善,欢迎诸位留言交流,批评指正~
Reference:
【1】http://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA)
【2】http://wenku.baidu.com/view/103b74768e9951e79b89274d.html
【3】http://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA)
【4】Christopher M. Bishop. 《Pattern Recognition and Machine Learning》chapter 1.6
【5】李鹤龄. 信息熵、玻尔兹曼熵以及克劳修斯熵之间的关系[J]. 大学物理. 第23卷第12期. 2004年12月
博主e-mail:[email protected]