Pólya计数小结

Burnside引理：记C(f)为在置换f下保持不变的着色方案的个数，那么本质不同的着色方案数位所有置换f的C(f)值的平均数。

如果求给定置换C(f)的方法为“一次判断每个着色方案是否在该置换下不变”由于每个方案包含p个“格子”的颜色信息，考察每个方案的复杂度为O(p)，考察所有n种着色方案的复杂度为O(np)，由于有s种置换方案，因此时间复杂度为O(nsp).

Polya定理：如果用k种颜色给有限集s着色，设m(f)为置换f的循环节的个数，则C(f)=k^m(f)（因为每个循环节之间的元素颜色应相同）

带入Burnside引理得到Polya定理。时间复杂度O(ps).

置换群性质：对于旋转置换群，群内置换的总个数显而易见是n个，第i个置换中循环节个数应该是gcd(n,i)个,且第i个元素于i+n/gcd*j个元素在同一循环节中；

使用欧拉函数优化，只处理n的因子i，ans+=Math.pow(s,i)*euler(n/i);(i|n,注意处理i*i=n时)

从几个简单的题目来理解一下以上两个定理：

poj 1286 Necklace of Bead / poj 2409 Let it Bead

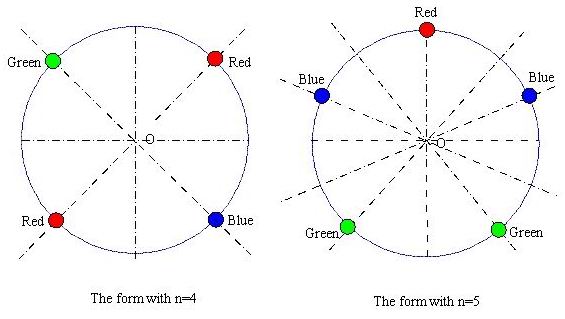
题意：s中颜色的珠子串成一条长度为n的项链，旋转和翻转同构的视为相同，问有多少种不同的项链。

解法：对于旋转置换，利用上述方法得到方案数；

对于翻转置换，上面的那个图给了很大提示，找循环节的关键是找对称轴。

当n为奇数，那么对称轴就是每个点和圆心的连线，共n条，那么显然除了这个点没变，其他的点都跟对称的那个点置换了，所以循环节的个数是（n-1）/2+1。

当n为偶数，那么对称轴有每个点和对面的点的连线，共n/2条，显然除了对称轴上的两个点，其余点都跟对面的点置换了循环节的个数是(n-2)/2+2，两个相邻点中点和圆心的连线也是n/2条，显然每个点都跟对面的点置换了，循环节的个数是n/2。

hdu 1812 Count the Tetris 
题意：边长为n的正方形，c中颜色，问不同的方案数。
解法：就是求对应的8个置换的循环节
1.旋转0度，循环节个数是 n*n
2.90度，（n*n+3）/4（奇数偶数都是成立）
3.180度，（n*n+1）/2
4.270度,(n*n+3)/4 和90度是一样的
5.两个对角线对称转动 n+(n*n-n)/2,注意这里是连个别忘了乘二
6.水平中线和竖直中线对称轴这里要分奇数偶数。
  奇数的时候 n+（n*n-n）/2 偶数的时候 n*n/2；

-------------------------------------------------------------------------------------

由于大多数计数问题都要对结果进行取模运算，当P不等于N时，可以在分母上乘上N的乘法逆元

k在mod意义下的成大逆元=pow(k % mod, mod - 2)而当N=P时，N的乘法逆元不存在，因此需要采取其他方法

poj 2154 Color

题意：N种颜色的珠子构成长度为N的项链，只记旋转置换

解法：利用颜色数等于珠子数且仅考虑旋转置换的特殊性进行mod运算，由于每个因子都是n的幂形式组成，因此颜色数s可看做n%p，每次进行i次幂运算时做i-1次，抵消最后需要除的n；

N=P时使用Rho-Pollard做二进制模乘运算代替乘法逆元做法

hdu 4048 Zhuge Liang's Stone Sentinel Maze

题意：给出m种不同重量的石子, 每一种石子的个数无穷多。从中选出N个石子，排成一个环，使得环上的石子重量的最大公约数为1. 旋转同构视为相同方案。

解法:问题转化为从m种数中找出n(循环节个数)个最大公约数为1的数字的排列数，于是想到找补集：满足最大公约数为2的充分必要条件是所选的数都能被2整除，满足最大公约数为2的充分必要条件是所选的数都能被2整除，满足最大公约数为6的方案被重复计算了，于是要容斥原理解决。

   即对于m个数，m*sqrt(m)时间内统计这m个数中能被i整除的个数nn[i]然后对于n', 假设g[i] = cnt[i] ^n，那么g[i]就是长度为N'的，最大公约数为i倍数的方案数。容斥时注意剪枝。

这题搞的很艰苦，代码见http://blog.csdn.net/kksleric/article/details/7821750

-----------------------------------------------------------------------------

有排列限制的Polya

poj 2888 Magic Bracelet

限制：只考虑中心对称，但是某些颜色的珠子不能相邻。

解法：根据Polya定理，sum=Sigma{Euler（n/i）*get（i）}；（n%i==0）其中get（i）是为i个循环节染色的方案数，不做限制时get(i)=s^i;但这里get(i)是要满足所有限制条件的染色方案，所以我们把m种颜色的关系画成一个无向图，而get(i)就是长度为 i 的回路的个数。即对邻接矩阵做i次幂后对角线元素的和。

Hdu 2865 Birthday Toy

限制条件：相邻的珠子颜色不能相同。

解法：如果颜色数少，可构造对角线为0其余元素为1的颜色矩阵，由于颜色数巨大，因此求get（i）时使用递推式，假设固定第一个珠子，设f(n)为最后一个珠子与第一个珠子颜色不相同的方案数，g(n)为最后一个珠子与第一个珠子颜色不相同的方案，则f(n)=f(n-1)*(s-2)+g(n-1)*(s-1),g(n)=f(n-1) 即f(n)=(s-2)*f(n-1)+(s-1)*f(n-2), f(n)=(s-1)^n+(s-1)*(-1)^n.再利用乘法逆元解决mod问题即可。

-------------------------------------------------------------------------------------

有个数限制的Polya

TJU 2795 The Queen's New Necklaces
这个题目就是对每种颜色的个数进行了限制，不过因为置换群很有规律,如果某个循环节的长度为k，那么k必须整除所有颜色个数时才能生效，对于有效的置换，使用多重集排列确定方案数。

UVa 11255 Necklace 

跟上题的限制相同，只不过加了翻转置换，对于旋转置换操作同上，对于翻转置换要分奇偶讨论，与poj 1286 类似。注意对称轴上的珠子颜色与置换无关，需要枚举。代码见下方

-------------------------------------------------------------------------------------

结合kmp求循环节的polya

hdu 4187 Alphabet Soup

题意：一个环上有N个可放物品的位置，S种物品每种数量不限，先给出N个位置的角度，问旋转置换下不同够的方案数。

解法：如果给出的角度不同，那么就等价于项链问题，如果角度不同，那么我们需要寻找一个最小的角度a，使这个环在旋转a°后与原环重合，因此可以将相邻两个位置见夹角作为字符串关键字，利用kmp求出最小循环节，得到循环节长度len后，相当于项链的长度变为了n/len，颜色数变为了S^len。

hdu 3869 Color the Simple Cycle 

解法：两次kmp找循环节，然后求得两循环节长度的最小公倍数，即为上题中的len

--------------------------------------------------------------------------------------------

非项链模型的polya

hdu 3441 Rotation

题意：将一个由A*A个方格组成的方块，分成k个B*B的方块和1个小方格后连乘一个由k+1个物体组成的环形物，如图，A=3时有两种分法。用C种颜色为每个方格染色，旋转得到的两种方案记为相同方案，问一共有多少种不同方案。

解法：如果将B*B的小正多边形看做一个整体，则B*B的方案数即外围“长度为k的项链”的颜色数，因此此题要嵌套两个polya分别对B*B和K+1个物体的方案数分别计算。

1.由于A巨大，因此不能提供枚举A*A-1的质因子确定B，首先将A*A-1化为(A+1)(A-1)然后分别求得A+1和A-1的质因子，然后将两个数的质因子分解结果合并，由于gcd(A+1,A-1)=1或2，因此对于A是奇数 的情况合并时需要合并2的幂数。由此得到若干对<B,K>；由于B*B*k=(A+1)(A-1),因此在枚举B是可以顺便处理k的质因子分解：初始化时与B*B的分解结果相同，每次dfs时B的质因子p增加delta倍，k的质因子p减少2delta倍。

2.对于一个B*B的正方形，共有四种置换(A,B,C,D)  (C,A,D,B) (D,C,B,A) (B,D,A,C)

          对于第1中置换，方案数为C^(B*B)

          对于第三种置换，如果B为偶数，根据前上面的B/2行便可得到下面的B/2行；若B为奇数，第B/2+1行任意染色，因此方案数C^(B*B+1)/2

          对于第二四种置换，如果B为偶数，左上角四分之一区域染色方案唯一确定整个B*B的染色方案；如果B为奇数，左上角(B+1)/2*(B-1)/2唯一确定其他三个角，同时中间格子随意染色，因此方案数为C^(B*B+3)/4

3.若B*B的不同方案是为c，则问题变为k个珠子的项链用c种颜色染色有多少种方案，通过k的质因子dfs求得所有可能的循环节个数得到方案数；同时中间的珠子有C中颜色，因此结果应乘C。

详见http://blog.csdn.net/kksleric/article/details/7786208

uva10601 Cubes

题意：给出正方体十二个棱的颜色，问不同够的正方体有多少个

解法：关键在于找出24种置换，然后就是一个普通的限制数量的polya了.

1、静止不动，那么就是12个循环，每个循环节长度为1

2、通过两个对立的顶点，分别旋转120，240，有4组顶点，在每一次旋转当中，可以发现分为4个循环，每个循环节长度为3，直观的说，就是有3条边是交换的，颜色必须一样

3、通过两个对立面的中心，分别旋转90，180，270度。有3组面

在每次旋转90度和270度的时候，可以发现分为3个循环，每个循环节长度为4

在每次旋转180度的时候，可以发现分为6个循环，每个循环节长度为2

4、通过两条对立的棱的中心，分别旋转180度，有6组棱

在每次旋转的时候，分为6个循环，每个循环节长度为2,注意枚举两条棱（固定不动）的颜色

-------------------------------------------------------------------------------------

较难的polya

　HDU 2481 Toy　　　　　　难度指数：★★★★ 
　　08年成都现场赛题目，难点在于求解递推关系。这个题目比较新颖的地方在于不是染色了，而是同构图计数。首先由于图形的特殊性可以推出递推关系(不是很好想)，然后利用矩阵求解。此外这个题目把同一循环节的缩成了一个珠子，利用这用方式来考虑问题，是一种新的思路。此外由于还是项链旋转，用到了一样的优化方式(凡是跟项链有关的就没有不考这个的了)。这个题目详尽的题解在这http://hi.baidu.com/spellbreaker/blog/item/1a7d9902ff6844e409fa93fb.html 
SGU 282 Isomorphism　　难度指数：★★★★★ 
　　这个题目比较新颖，置换非常多，因此需要一些巧妙的方法优化。置换的个数达到了n!，但是可以通过搜索来枚举每个循环节的长度，把复杂度降到了求解n的分拆数方案数那么多。设n = L1 + L2 + ... + Lm，那么满足这个类型的置换个数是n! / (L1 * L2 * ... * Lm * k1! * k2! * ... * kt!)，其中t是不同的循环节长度的个数，ki是每种循环节长度，这个公式的大体思想就是：首先因为是置换，因此每个循环节内的数是固定的，把一个循环节内的数看成1个就变成了多重集的排列，但是每个循环节(Li)内，第一个数有(Li - 1)种选法(只要不是自己就行)，第二个数有(Li - 2)种选法，依次类推，因此每个循环节还要乘以(Li - 1)!；之后因为对于两个同样长度的循环节，一旦选定了位置，其实不可以互换，因此要把多余的方案除掉，最后就是上述的公式。找出了置换的个数，接下来的问题就是，因为题目是对边染色，因此要把点置换映射成边置换。通过小范围的观察可以发现(具体证明不太会)：一个长度为L的点循环节对应[L/2]个边循环节，两个长度分别是L1、L2的点循环节对应gcd(L1, L2)个边循环节。因为polya定理同一循环节内染色相同，因此不必关心对应后的边循环节长度，只要知道个数即可(这一点很巧妙)，所以这样映射便可以求出结果。最后要注意的是题目说明了模一个素数，因此可以预处理出逆元来。
SPOJ 422 Transposing is Even More Fun　　　　难度指数：★★★★★ 
　　这个题目需要一些观察力。把地址转置之后对应的写下来，会发现，一个长度为L循环节只需要移动L-1次(利用一个元素进行对换)，这样假设有k个循环节，那么答案就是2 ^ (a + b) - k，关键问题是如何求k。循环节的个数其实就是相当于地址右移若干个b位后本质不同的地址个数，这样就划归到了polya定理的范畴。长度为a+b的地址一共可以右移(a + b) / (a, b)次(之后就出现循环了)，因此这就是置换的个数。现在分别考虑每个置换下不同的地址个数，设g = gcd(a, b)，那么可以看成一共有(a + b) / g个珠子，每个大小是2 ^ g，这样如果移动i下，那么对应的本质不同的地址个数是(2 ^ g) ^ gcd(i, (a + b) / g)多个(类似于项链旋转)，最后累加然后除以总置换数即可。
　　然后的问题就是如何高效求解，由于数据组数非常多，利用欧拉函数以O(sqrt(a + b))的复杂度依然TLE。后来参照cyx的论文，实现了一个理论复杂度看似很高但是实际很快的方法。记f[i]表示满足gcd(i, (a + b) / g)是i的个数，先把总数分配给1，然后对(a + b) / g因式分解，用类似bfs的方法，扩展当前状态，如果从x扩展到了xp，那么就把x总数的1/p分给xp，注意不要重复扩展，利用一个单调队列让每个和数都唯一的被它的最小素因子扩展一次即可。这个方法复杂度难以估计但是很快出解。 

UVa 11255 Necklace ：

import java.math.BigInteger; import java.util.Scanner; public class NeckLace11255 { int prime[] = new int[10010], count[] = new int[10010], cnt; void divide(int n) { cnt = 0;// 质因子数目 int mx = (int) (Math.sqrt(n) + 3); if (n < mx) mx = n; for (int i = 2; i < mx; i++) { if (n == 1) break; if (n % i == 0) { prime[++cnt] = i; count[cnt] = 0; while (n % i == 0) { n /= i; count[cnt]++; } } } if (n != 1) { prime[++cnt] = n; count[cnt] = 1; } } BigInteger get(int k) {// 循环节数目为k的置换下不同的方案 int value=n/k; for(int i=1;i<=c;i++) if(color[i]%value!=0) return BigInteger.ZERO; else temp[i]=color[i]/value; BigInteger sum=fac[k]; for(int i=1;i<=c;i++) sum=sum.divide(fac[temp[i]]); return sum; } int n, c; BigInteger ans; int temp[]=new int[110]; void dfs(int now, int value, int euler) { while(value==0) now++; if (now == cnt + 1) {// value是n的因子 ans=ans.add(BigInteger.valueOf(euler).multiply(get(n/value))); return; } dfs(now + 1, value, euler); int temp = prime[now]; for (int i = 1; i <= count[now]; i++) { dfs(now + 1, value * temp, euler*(prime[now] - 1) * (temp / prime[now]));// muti_mod!!! temp *= prime[now]; } } void polya() { ans =BigInteger.valueOf(0); divide(n); dfs(1, 1, 1); } void flip(){ if(n%2==1){ n--; for(int i=1;i<=3;i++){ color[i]--; if(color[i]>=0) ans=ans.add(get(n/2).multiply(BigInteger.valueOf(n+1))); color[i]++; } n++; } else { ans=ans.add(get(n/2).multiply(BigInteger.valueOf(n/2))); n-=2; for(int i=1;i<=3;i++) for(int j=1;j<=3;j++){ color[i]--; color[j]--; if(color[i]>=0&&color[j]>=0) ans=ans.add(get(n/2).multiply(BigInteger.valueOf(n/2+1))); color[i]++; color[j]++; } n+=2; } } Scanner scan=new Scanner(System.in); int color[]=new int[110]; BigInteger fac[]=new BigInteger[1010]; void init(){ fac[0]=BigInteger.ONE; for(int i=1;i<1010;i++){ fac[i]=fac[i-1].multiply(BigInteger.valueOf(i)); } } void run(){ int cas=scan.nextInt(); init(); c=3; while(cas-->0){ n=0; for(int i=1;i<=c;i++) { color[i]=scan.nextInt(); n+=color[i]; } polya(); flip(); ans=ans.divide(BigInteger.valueOf(n*2)); System.out.println(ans); } } public static void main(String[] args) { new NeckLace11255().run(); } } 

hdu 4187 Alphabet Soup

import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.io.StreamTokenizer; import java.util.Arrays; public class Soup4187 { int prime[] = new int[10010], count[] = new int[10010], cnt; void divide(int n) { cnt = 0;// 质因子数目 int mx = (int) (Math.sqrt(n) + 3); if (n < mx) mx = n; for (int i = 2; i < mx; i++) { if (n == 1) break; if (n % i == 0) { prime[++cnt] = i; count[cnt] = 0; while (n % i == 0) { n /= i; count[cnt]++; } } } if (n != 1) { prime[++cnt] = n; count[cnt] = 1; } } long pow(long x, int p) { long ans = 1; while (p > 0) { if ((p & 1) == 1) ans = (ans * x) % mod; p >>= 1; x = (x * x) % mod; } return ans; } long inv(int k) {// k在摸mod意义下的乘法逆元 return pow(k % mod, mod - 2) % mod; } long get(int k) {// 循环节个数为k的置换下不同的方案 return pow(c, k); } int n, mod = 100000007; long ans,c; void dfs(int now, int value, int euler) { if (now == cnt + 1) {// value是n的因子 ans += (euler * get(n / value)) % mod;// muti_mod!!! ans %= mod; return; } dfs(now + 1, value, euler); int temp = prime[now]; for (int i = 1; i <= count[now]; i++) { dfs(now + 1, value * temp, euler * (prime[now] - 1) * (temp / prime[now]) % mod);// muti_mod!!! temp *= prime[now]; temp %= mod; } } long polya() { ans = 0; divide(n); dfs(1, 1, 1); ans=ans*inv(n)% mod; return ans; } int next[]=new int[360010]; int kmp(){ next[0]=0; int j=0; for(int i=2;i<=n;i++){ while(j>0&&angle[j]!=angle[i-1]) j=next[j-1]; if(angle[j]==angle[i-1]) j++; next[i-1]=j; } int len=n-next[n-1]; if(n%len==0) return len; return n; } int angle[]=new int[360010]; void run() throws IOException { while (true) { c = nextInt(); n = nextInt(); if(c==-1&&n==-1) break; for(int i=0;i<n;i++) angle[i]=nextInt(); Arrays.sort(angle,0,n); int temp=angle[n-1]; for(int i=n-1;i>0;i--) angle[i]-=angle[i-1]; angle[0]+=360000-temp; int k=kmp(); n/=k; c=pow(c,k); System.out.println(polya()); } } StreamTokenizer in = new StreamTokenizer(new BufferedReader( new InputStreamReader(System.in))); int nextInt() throws IOException { in.nextToken(); return (int) in.nval; } public static void main(String[] args) throws IOException { new Soup4187().run(); } } 

uva 

10601 Cubes

import java.util.Arrays; import java.util.Scanner; public class Cube { int fac[]=new int[20]; void init(){ fac[0]=1; for(int i=1;i<=12;i++) fac[i]=fac[i-1]*i; } long cal(int k){//循环节长度 k long res=0; for(int i=0;i<6;i++) if(color[i]%k!=0) return 0; else temp[i]=color[i]/k; res=fac[n/k]; for(int i=0;i<6;i++) res/=fac[temp[i]]; return res; } long rotate(){ int res=0; n=10; for(int i=0;i<6;i++) for(int j=0;j<6;j++) { color[i]--; color[j]--; if(color[i]>=0&&color[j]>=0) res+=cal(2)*6; color[i]++; color[j]++; } n=12; return res; } int color[]=new int[6],temp[]=new int[6],n=12; Scanner scan=new Scanner(System.in); void run(){ int cas=scan.nextInt(); init(); while(cas-->0){ Arrays.fill(color, 0); for(int i=0;i<12;i++) color[scan.nextInt()-1]++; long ans=cal(1); ans+=cal(3)*8; ans+=cal(4)*6; ans+=cal(2)*3; ans+=rotate(); System.out.println(ans/24); } } public static void main(String[] args) { new Cube().run(); } }