通过一些通信方式传输的数据(比如:串口传输),有时候会保存为char类型的数据数据,我们需要把char数组中的所有数据转化为int整数,方法一是直接通过移位运算来实现:charc[4]={0x3,0x0f,0xf,0xf};chart;intnum=0;intlen=sizeof(c)/2;chard[sizeof(c)/2]{0};for(inti=0,j=0;j
ROS2软件架构全面解析-学习如何设计通信中间件框架
chinamaoge
ROS2DDS通信中间件ROS2ROS通信中间件
前言ROS(RobotOperatingSystem)2是一个用于开发机器人应用的软件平台,也称为机器人软件开发工具包(SDK)。ROS2是ROS1的迭代升级版本,最主要的升级点是引入DDS(DataDistributionService)为基础的底层通信系统。为解决ROS1存在主要几个缺陷:为解决一个主节点通信故障(ROSMaster),需要对所有现有的Client库进行单独的补丁处理,并且每个
【信息学奥赛一本通 C++题解】1286:怪盗基德的滑翔翼
信奥大黄
信息学奥赛一本通c++算法
信息学奥赛一本通(C++版)在线评测系统基础算法第一节动态规划的基本模型1286:怪盗基德的滑翔翼1.理解题意同学们,我们一起来看怪盗基德遇到的这个有趣问题哦。怪盗基德成功偷到了钻石,可倒霉的是他的滑翔翼动力装置被柯南破坏了。现在他在一个城市里,这个城市有一排建筑,一共有N幢,而且每幢建筑的高度都不一样呢。基德可以从这一排建筑中的任意一幢的顶部开始他的逃跑旅程哦。不过他有两个限制条件:一是他只能朝
C++调用CPLEX踩过的小坑~
blackms1023
c++
最近在使用VisualStudio2015调用CPLEX进行一些基础问题的求解,初学小白,完全没经验,遇到N多问题,踩了好多坑,在此分享一下!希望可以给后其他研究者提供一neinei学习的经验!1.关于CPLEX中默认变量的问题CPLEX中默认变量为非负值,故在实际编码过程中如若不为变量指定下界为负无穷,且变量存在负值情况,则会出现计算数据错误的情况。具体解决方法就是在初始化的过程中,为其指定一个
如何代写一份成熟的商业计划书?
TNT_13302909089
代写商业计划书商业计划书写一份成熟的商业计划书
商业计划书可以用来介绍企业的价值,从而吸引到投资、员工、战略合作伙伴,或包括政府在内的其他利益相关者。一份成熟的商业计划书不但能够能描述出你公司的成长历史,展现出未来的成长方向和愿景,还将量化出潜在盈利能力。这都需要你对自己公司有一个通盘的了解,对所有存在的问题都有所思考,对可能存在的隐患做好预案,并能够提出行之有效的工作计划。融资商业计划书也体现了上级对下级的承诺。公司战略的得以展开,必然意味着
商业计划书代写?别浪费钱
TNT_13302909089
商业计划书代写商业计划书创业计划书
商业计划书包含的范围很广,但一般离不开以下题目:经营者的理念、市场、客户、比较优势、管理团队、财务预测、风险因素等等。对市场的分析应由大入小,从宏观到微观,以数据为基础,深刻的描述公司/项目在市场中将争取的定位。对比较优势,应在非常清楚本身强弱情况及竞争对手的战略而作分析。至于管理团队,应从各人的背景及经验分析其对公司/项目中不同岗位的作用。财务预测是关键的,应将绝大部分的假设及其所引致的财务影响
什么是可行性研究报告,可研报告代写指南,包含内容,用途等详细说明
TNT_13302909089
人工智能大数据深度学习机器学习数据分析
可行性研究报告是一种针对拟议中的项目、投资、技术、业务或其他类型的计划进行系统性分析和评估的书面报告。该报告的主要目的是全面、客观、科学地分析项目的可行性,包括技术可行性、经济可行性、社会可行性、环境可行性等多个维度,以确定该项目是否值得实施,以及实施中可能遇到的问题和解决方案。主要内容项目概述:介绍项目的背景、目的、目标、范围等基本信息。市场需求分析:评估目标市场的需求、市场规模、增长潜力以及竞
[C#]C#使用yolov8的目标检测tensorrt模型+bytetrack实现目标追踪
FL1623863129
深度学习c#YOLO目标检测
【测试通过环境】win10x64vs2019cuda11.7+cudnn8.8.0TensorRT-8.6.1.6opencvsharp==4.9.0.NETFramework4.7.2NVIDIAGeForceRTX2070Super版本和上述环境版本不一样的需要重新编译TensorRtExtern.dll,TensorRtExtern源码地址:TensorRT-CSharp-API/src/T
一键启动多个软件,开启高效办公新时代
KJ-拾荒者
生活职场和发展性能优化经验分享安全
在快节奏的现代生活中,我们的电脑上安装了各种各样的软件,从办公软件到娱乐软件,从社交软件到学习软件。然而,每次打开电脑后,逐一启动这些软件不仅浪费时间,还会影响我们的心情和工作效率。今天,我要为大家介绍一款能够解决这一问题的神奇软件——一键启动多个软件,它将彻底改变你的电脑使用体验。一、高效便捷,一键启动这款软件的最大亮点就是它的高效便捷性。你可以将常用的软件添加到启动列表中,然后只需轻轻一点,就
壁纸样机神器:个性化壁纸宣传生成器,提升你的宣发效率
2401_89910411
数码相机
在数字时代,壁纸不仅是手机或电脑屏幕的装饰,更是个人品味和创意的展示窗口。但你是否想过,自己也能轻松设计出专业级的壁纸,并将其转化为独特的作品?今天,就让我们一起探索壁纸样机神器的神奇魅力,开启你的壁纸创作之旅。为什么你需要壁纸样机神器?在社交媒体和数字内容盛行的今天,壁纸设计已经不仅仅是一种爱好,更是一种可以变现的技能。无论是个人创作者、设计师还是品牌推广者,一款好的壁纸设计工具都能为你带来巨大
《C#与Unity携手,构建沉浸式虚拟现实三维场景》
墨夶
C#学习资料1c#unityvr
随着虚拟现实(VirtualReality,VR)技术的迅猛发展,越来越多的开发者开始探索如何利用这一新兴媒介创造更加引人入胜的应用程序。在众多开发工具中,Unity以其强大的功能和易用性脱颖而出,成为了VR应用开发者的首选平台之一。而作为Unity官方支持的主要编程语言——C#,则为开发者提供了实现复杂逻辑、优化性能的强大手段。本文将详细介绍如何使用C#结合Unity来构建一个完整的虚拟现实三维
wsl使用
_DT9825
ubuntu
安装首先在电脑开始界面搜索启用或关闭window功能,勾选如图所示的选项,即可配置成功wsl环境。1、2、打开命令窗口,cmd或powershell,输入wsl--install即可安装。(默认安装Ubuntu版本)输入wsl--list--online可以查看历史发行版本。如果要安装特定版本wsl--install-dXXXX(XXXX为版本名称)例如wsl--install-dDebianws
如何提升爬虫获取数据的准确性?
小爬虫程序猿
爬虫
提升爬虫获取数据的准确性是确保数据分析和后续应用有效性的关键。以下是一些经过验证的方法和最佳实践,可以帮助提高爬虫数据的准确性:1.数据清洗数据清洗是提升数据准确性的重要步骤,主要包括去除重复数据、处理缺失值和异常值。去除重复数据:重复数据会影响分析结果的准确性,可以通过pandas库的drop_duplicates()方法删除重复数据。importpandasaspddf=pd.DataFram
婚恋相亲交友父母牵线搭桥红娘助手小程序系统
狂团商城小师妹
博纳miui52086微信小程序微信公众平台微信
婚恋相亲交友父母牵线搭桥红娘助手小程序系统助力婚恋平台精准获客与流量提升一、行业背景与用户需求分析随着社会节奏加快和单身人口增长,婚恋相亲交友已成为刚需市场。据统计,中国适婚单身人群已超2.4亿,其中超过60%的年轻人依赖线上平台解决婚恋需求。然而,传统相亲模式存在匹配效率低、信任度不足等问题,而父母牵线搭桥与红娘助手小程序系统的结合,正成为解决痛点的创新方案。此类平台需满足三大核心需求:精准匹配
四平方和(多种解法)
delim6
算法数据结构哈希算法c++
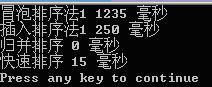
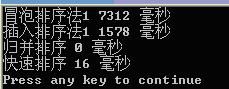
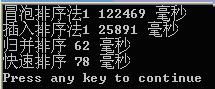
注意,会列举过不了的一些思路四平方和四平方和定理,又称为拉格朗日定理:每个正整数都可以表示为至多44个正整数的平方和。如果把0包括进去,就正好可以表示为4个数的平方和。比如:5=0^2+0^2+1^2+2^27=1^2+1^2+1^2+2^2对于一个给定的正整数,可能存在多种平方和的表示法。要求你对4个数排序:0≤a≤b≤c≤d并对所有的可能表示法按a,b,c,d为联合主键升序排列,最后输出第一个
商协会管理系统:沃德商协会管理系统微信小程序公众号
狂团商城小师妹
博纳miui52086微信小程序小程序微信公众平台
智慧化会员体系在线入会、会费缴纳、到期提醒、会员管理、消息群发、线上证书、会员通讯录、有效供需匹配等。智敏化内容运营活动接龙,问卷调查,党建新闻资讯发布,多方位满足会员内容信息运营。智能化活动构建为商会提供多种活动营解决方案,活动发布、活动推广、活动费用、在线报名。入会方式支持多种商协会缴费入会方式,实现商协会智能化管理1、线上缴费入会2、线下缴费入会3、后台添加入会会员信息充足情况下,可进行单个
同城组局旅游组局搭子论坛系统
狂团商城小师妹
博纳miui52086微信小程序小程序微信公众平台
同城组局旅游组局搭子论坛系统,作为一款集旅游组局、社交互动与信息服务于一体的综合性平台,其组局系统实现了无限开启的灵活性与便捷性,为用户提供了前所未有的组局体验。该系统基于先进的TP6框架与Mysql8数据库,并融入了Redis高并发架构,确保了在高流量、高并发场景下的稳定运行与快速响应。这一技术选型不仅提升了系统的整体性能,更为用户带来了流畅无阻的使用感受。在功能性方面,该系统展现出了极高的实用
学C++还是学Java?做软件研发还需掌握哪些知识和技能?_c+
2401_84160087
程序员c++javac语言
1.1、Java和C++都很有前途1.2、Java的应用领域与使用场景1.3、C++的应用领域与使用场景1.4、如何选择2、需要掌握的知识和技能2.1、掌握一些基础的网络知识2.2、熟悉一些常用的SQL语句2.3、了解Linux系统,掌握常用的Linux命令2.4、学习汇编语言相关的内容2.5、学习一些其他的专业课程3、最后最近和一些高校的学生朋友交流,他们打算毕业后从事软件研发的工作,但目前有些
软考高级《系统架构设计师》知识点(五)
Ritchie里其
系统架构
计算机网络网络概述和模型计算机网络是计算机技术与通信技术相结合的产物,它实现了远程通信、远程信息处理和资源共享。计算机网络的功能:数据通信、资源共享、管理集中化、实现分布式处理、负载均衡。网络性能指标:速率、带宽(频带宽度或传送线路速率)、吞吐量、时延、往返时间、利用率。网络非性能指标:费用、质量、标准化、可靠性、可扩展性、可升级性、易管理性和可维护性。通信技术:计算机网络是利用通信技术将数据从一
Java和SQL测试、性能监控中常用工具
2301_79306982
javasqlselenium单元测试压力测试集成测试
下面我会详细列举一些在Java和SQL测试、调试、性能监控中常用的工具,并结合项目中提到的各个技术点说明如何选择合适的工具和方法。一、Java项目常用的测试、调试与性能监控工具单元测试与集成测试:JUnit/TestNG:用于编写单元测试和集成测试。比如在SpringBoot项目中,可以使用JUnit对各个服务进行功能测试。Mockito:用于模拟依赖项,帮助隔离单元测试时的环境。静态代码分析:S
html+css网页设计,我的网站
软件技术NINI
html/css笔记javascripthtmlcss
一、技术简介HTML:超文本标记语言(HyperTextMarkupLanguage),用于创建网页的基本结构和内容。CSS:层叠样式表(CascadingStyleSheets),用于设置网页的样式和布局,包括字体、颜色、边距、对齐方式等。JavaScript:一种用于创建动态和交互式网页的脚本语言。通过JavaScript,可以实现网页的动画效果、表单验证、数据交互等功能。二、创建多页网站的基
c# —— StringBuilder 类
山水CAD筑梦人
C#学习笔记java开发语言
StringBuilder类是C#和其他一些基于.NETFramework的编程语言中的一个类,它位于System.Text命名空间下。StringBuilder类表示一个可变的字符序列,它是为了提供一种比直接使用字符串连接操作更加高效的方式来构建或修改字符串。与C#中的string类型不同,string是不可变的,这意味着每次对字符串进行修改(如拼接、替换字符等)时,都会创建一个新的字符串对象。
【花雕学编程】Arduino JSON 之合理设计 API 的架构
驴友花雕
开源硬件json嵌入式硬件单片机c++合理设计API的架构ArduinoJSON
Arduino是一个开放源码的电子原型平台,它可以让你用简单的硬件和软件来创建各种互动的项目。Arduino的核心是一个微控制器板,它可以通过一系列的引脚来连接各种传感器、执行器、显示器等外部设备。Arduino的编程是基于C/C++语言的,你可以使用ArduinoIDE(集成开发环境)来编写、编译和上传代码到Arduino板上。Arduino还有一个丰富的库和社区,你可以利用它们来扩展Ardui
c#模拟鼠标点击左键
王焜棟琦
C#c#
c#模拟鼠标点击左键,这里调用的是windows系统函数,usingSystem;usingSystem.Collections.Generic;usingSystem.Linq;usingSystem.Runtime.InteropServices;usingSystem.Text;usingSystem.Threading.Tasks;namespaceWindowsFormsAppHalco
图论- 经典最小生成树算法
左灯右行的爱情
图论算法
最小生成树算法什么是最小生成树Kruskal算法关键代码实现Prim最小生成树算法Kruskal和Prim算法的区别为什么Prim算法不需要判断成环,但Kruskal需要什么是最小生成树在图中找一棵包含图中所有节点的树,且权重和最小的那棵树就叫最小生成树.如下:右侧生成树的权重和显然比左侧生成树的权重和要小。(但是它并不是最小的,这里只是比较一下不同的树)Kruskal算法最小生成树是若干条边的集
沃德校园助手系统php+uniapp
狂团商城小师妹
博纳miui52086uni-app微信小程序微信公众平台
一款基于FastAdmin+ThinkPHP+Uniapp开发的为校园团队提供全套的技术系统及运营的方案(目前仅适配微信小程序),可以更好的帮助你打造自己的线上助手平台。成本低,见效快。各种场景都可以自主选择服务。更新日志V1.2.1小程序需要更新【新增】1.默认学校排序方式(距离和时间)2.自定义服务标题和排序3.超市外卖库存和限购功能4.订单分享功能【优化】1.下单时默认手机号可修改2.下单时
ABB机器人的二次开发
Mountain and sea
机器人算法c语言学习自动化
ABB机器人的二次开发可以通过多种方式实现,主要涉及编程接口、通信协议和开发工具。以下是详细的步骤和方法:1.基础准备确认RobotWare选项:确保机器人控制器安装了必要的选项,如:PCInterface(用于PCSDK通信)RobotWebServices(RESTAPI支持)Fieldbus选项(如Profinet、EtherNet/IP)权限设置:在示教器上将用户权限设置为“专家模式”或更
DeepSeek与ChatGPT:AI语言模型的全面对决
四念处茫茫
AI人工智能chatgpt语言模型
DeepSeek与ChatGPT:AI语言模型的全面对决引言:AI语言模型的时代浪潮一、认识DeepSeek与ChatGPT(一)DeepSeek:国产新星的崛起(二)ChatGPT:AI界的开拓者二、DeepSeek与ChatGPT使用指南(一)DeepSeek使用全攻略1.多种使用途径介绍2.功能使用技巧(二)ChatGPT使用秘籍1.访问与使用流程三、深度剖析:功能大比拼(一)文本创作能力(
VMware Workstation 11 或者 VMware Player 7安装MAC OS X 10.10 Yosemite
iwindyforest
vmwaremac os10.10workstationplayer
最近尝试了下VMware下安装MacOS 系统,
安装过程中发现网上可供参考的文章都是VMware Workstation 10以下, MacOS X 10.9以下的文章,
只能提供大概的思路, 但是实际安装起来由于版本问题, 走了不少弯路, 所以我尝试写以下总结, 希望能给有兴趣安装OSX的人提供一点帮助。
写在前面的话:
其实安装好后发现, 由于我的th
关于《基于模型驱动的B/S在线开发平台》源代码开源的疑虑?
deathwknight
JavaScriptjava框架
本人从学习Java开发到现在已有10年整,从一个要自学 java买成javascript的小菜鸟,成长为只会java和javascript语言的老菜鸟(个人邮箱:
[email protected])
一路走来,跌跌撞撞。用自己的三年多业余时间,瞎搞一个小东西(基于模型驱动的B/S在线开发平台,非MVC框架、非代码生成)。希望与大家一起分享,同时有许些疑虑,希望有人可以交流下
平台
创建Web工程,使用eclipse ee创建maven web工程 1.右键项目,选择Project Facets,点击Convert to faceted from 2.更改Dynamic Web Module的Version为2.5.(3.0为Java7的,Tomcat6不支持). 如果提示错误,可能需要在Java Compiler设置Compiler compl
主管???
Array_06
工作
转载:http://www.blogjava.net/fastzch/archive/2010/11/25/339054.html
很久以前跟同事参加的培训,同事整理得很详细,必须得转!
前段时间,公司有组织中高阶主管及其培养干部进行了为期三天的管理训练培训。三天的课程下来,虽然内容较多,因对老师三天来的课程内容深有感触,故借着整理学习心得的机会,将三天来的培训课程做了一个
python内置函数大全
2002wmj
python
最近一直在看python的document,打算在基础方面重点看一下python的keyword、Build-in Function、Build-in Constants、Build-in Types、Build-in Exception这四个方面,其实在看的时候发现整个《The Python Standard Library》章节都是很不错的,其中描述了很多不错的主题。先把Build-in Fu
JSP页面通过JQUERY合并行
357029540
JavaScriptjquery
在写程序的过程中我们难免会遇到在页面上合并单元行的情况,如图所示
如果对于会的同学可能很简单,但是对没有思路的同学来说还是比较麻烦的,提供一下用JQUERY实现的参考代码
function mergeCell(){
var trs = $("#table tr");
&nb
Java基础
冰天百华
java基础
学习函数式编程
package base;
import java.text.DecimalFormat;
public class Main {
public static void main(String[] args) {
// Integer a = 4;
// Double aa = (double)a / 100000;
// Decimal
unix时间戳相互转换
adminjun
转换unix时间戳
如何在不同编程语言中获取现在的Unix时间戳(Unix timestamp)? Java time JavaScript Math.round(new Date().getTime()/1000)
getTime()返回数值的单位是毫秒 Microsoft .NET / C# epoch = (DateTime.Now.ToUniversalTime().Ticks - 62135
作为一个合格程序员该做的事
aijuans
程序员
作为一个合格程序员每天该做的事 1、总结自己一天任务的完成情况 最好的方式是写工作日志,把自己今天完成了什么事情,遇见了什么问题都记录下来,日后翻看好处多多
2、考虑自己明天应该做的主要工作 把明天要做的事情列出来,并按照优先级排列,第二天应该把自己效率最高的时间分配给最重要的工作
3、考虑自己一天工作中失误的地方,并想出避免下一次再犯的方法 出错不要紧,最重
由html5视频播放引发的总结
ayaoxinchao
html5视频video
前言
项目中存在视频播放的功能,前期设计是以flash播放器播放视频的。但是现在由于需要兼容苹果的设备,必须采用html5的方式来播放视频。我就出于兴趣对html5播放视频做了简单的了解,不了解不知道,水真是很深。本文所记录的知识一些浅尝辄止的知识,说起来很惭愧。
视频结构
本该直接介绍html5的<video>的,但鉴于本人对视频
解决httpclient访问自签名https报javax.net.ssl.SSLHandshakeException: sun.security.validat
bewithme
httpclient
如果你构建了一个https协议的站点,而此站点的安全证书并不是合法的第三方证书颁发机构所签发,那么你用httpclient去访问此站点会报如下错误
javax.net.ssl.SSLHandshakeException: sun.security.validator.ValidatorException: PKIX path bu
Jedis连接池的入门级使用
bijian1013
redisredis数据库jedis
Jedis连接池操作步骤如下:
a.获取Jedis实例需要从JedisPool中获取;
b.用完Jedis实例需要返还给JedisPool;
c.如果Jedis在使用过程中出错,则也需要还给JedisPool;
packag
变与不变
bingyingao
不变变亲情永恒
变与不变
周末骑车转到了五年前租住的小区,曾经最爱吃的西北面馆、江西水饺、手工拉面早已不在,
各种店铺都换了好几茬,这些是变的。
三年前还很流行的一款手机在今天看起来已经落后的不像样子。
三年前还运行的好好的一家公司,今天也已经不复存在。
一座座高楼拔地而起,
【Scala十】Scala核心四:集合框架之List
bit1129
scala
Spark的RDD作为一个分布式不可变的数据集合,它提供的转换操作,很多是借鉴于Scala的集合框架提供的一些函数,因此,有必要对Scala的集合进行详细的了解
1. 泛型集合都是协变的,对于List而言,如果B是A的子类,那么List[B]也是List[A]的子类,即可以把List[B]的实例赋值给List[A]变量
2. 给变量赋值(注意val关键字,a,b
Nested Functions in C
bookjovi
cclosure
Nested Functions 又称closure,属于functional language中的概念,一直以为C中是不支持closure的,现在看来我错了,不过C标准中是不支持的,而GCC支持。
既然GCC支持了closure,那么 lexical scoping自然也支持了,同时在C中label也是可以在nested functions中自由跳转的
Java-Collections Framework学习与总结-WeakHashMap
BrokenDreams
Collections
总结这个类之前,首先看一下Java引用的相关知识。Java的引用分为四种:强引用、软引用、弱引用和虚引用。
强引用:就是常见的代码中的引用,如Object o = new Object();存在强引用的对象不会被垃圾收集
读《研磨设计模式》-代码笔记-解释器模式-Interpret
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
package design.pattern;
/*
* 解释器(Interpreter)模式的意图是可以按照自己定义的组合规则集合来组合可执行对象
*
* 代码示例实现XML里面1.读取单个元素的值 2.读取单个属性的值
* 多
After Effects操作&快捷键
cherishLC
After Effects
1、快捷键官方文档
中文版:https://helpx.adobe.com/cn/after-effects/using/keyboard-shortcuts-reference.html
英文版:https://helpx.adobe.com/after-effects/using/keyboard-shortcuts-reference.html
2、常用快捷键
Maven 常用命令
crabdave
maven
Maven 常用命令
mvn archetype:generate
mvn install
mvn clean
mvn clean complie
mvn clean test
mvn clean install
mvn clean package
mvn test
mvn package
mvn site
mvn dependency:res
shell bad substitution
daizj
shell脚本
#!/bin/sh
/data/script/common/run_cmd.exp 192.168.13.168 "impala-shell -islave4 -q 'insert OVERWRITE table imeis.${tableName} select ${selectFields}, ds, fnv_hash(concat(cast(ds as string), im
Java SE 第二讲(原生数据类型 Primitive Data Type)
dcj3sjt126com
java
Java SE 第二讲:
1. Windows: notepad, editplus, ultraedit, gvim
Linux: vi, vim, gedit
2. Java 中的数据类型分为两大类:
1)原生数据类型 (Primitive Data Type)
2)引用类型(对象类型) (R
CGridView中实现批量删除
dcj3sjt126com
PHPyii
1,CGridView中的columns添加
array(
'selectableRows' => 2,
'footer' => '<button type="button" onclick="GetCheckbox();" style=&
Java中泛型的各种使用
dyy_gusi
java泛型
Java中的泛型的使用:1.普通的泛型使用
在使用类的时候后面的<>中的类型就是我们确定的类型。
public class MyClass1<T> {//此处定义的泛型是T
private T var;
public T getVar() {
return var;
}
public void setVa
Web开发技术十年发展历程
gcq511120594
Web浏览器数据挖掘
回顾web开发技术这十年发展历程:
Ajax
03年的时候我上六年级,那时候网吧刚在小县城的角落萌生。传奇,大话西游第一代网游一时风靡。我抱着试一试的心态给了网吧老板两块钱想申请个号玩玩,然后接下来的一个小时我一直在,注,册,账,号。
彼时网吧用的512k的带宽,注册的时候,填了一堆信息,提交,页面跳转,嘣,”您填写的信息有误,请重填”。然后跳转回注册页面,以此循环。我现在时常想,如果当时a
openSession()与getCurrentSession()区别:
hetongfei
javaDAOHibernate
来自 http://blog.csdn.net/dy511/article/details/6166134
1.getCurrentSession创建的session会和绑定到当前线程,而openSession不会。
2. getCurrentSession创建的线程会在事务回滚或事物提交后自动关闭,而openSession必须手动关闭。
这里getCurrentSession本地事务(本地
第一章 安装Nginx+Lua开发环境
jinnianshilongnian
nginxluaopenresty
首先我们选择使用OpenResty,其是由Nginx核心加很多第三方模块组成,其最大的亮点是默认集成了Lua开发环境,使得Nginx可以作为一个Web Server使用。借助于Nginx的事件驱动模型和非阻塞IO,可以实现高性能的Web应用程序。而且OpenResty提供了大量组件如Mysql、Redis、Memcached等等,使在Nginx上开发Web应用更方便更简单。目前在京东如实时价格、秒
HSQLDB In-Process方式访问内存数据库
liyonghui160com
HSQLDB一大特色就是能够在内存中建立数据库,当然它也能将这些内存数据库保存到文件中以便实现真正的持久化。
先睹为快!
下面是一个In-Process方式访问内存数据库的代码示例:
下面代码需要引入hsqldb.jar包 (hsqldb-2.2.8)
import java.s
Java线程的5个使用技巧
pda158
java数据结构
Java线程有哪些不太为人所知的技巧与用法? 萝卜白菜各有所爱。像我就喜欢Java。学无止境,这也是我喜欢它的一个原因。日常
工作中你所用到的工具,通常都有些你从来没有了解过的东西,比方说某个方法或者是一些有趣的用法。比如说线程。没错,就是线程。或者确切说是Thread这个类。当我们在构建高可扩展性系统的时候,通常会面临各种各样的并发编程的问题,不过我们现在所要讲的可能会略有不同。
开发资源大整合:编程语言篇——JavaScript(1)
shoothao
JavaScript
概述:本系列的资源整合来自于github中各个领域的大牛,来收藏你感兴趣的东西吧。
程序包管理器
管理javascript库并提供对这些库的快速使用与打包的服务。
Bower - 用于web的程序包管理。
component - 用于客户端的程序包管理,构建更好的web应用程序。
spm - 全新的静态的文件包管
避免使用终结函数
vahoa.ma
javajvmC++
终结函数(finalizer)通常是不可预测的,常常也是很危险的,一般情况下不是必要的。使用终结函数会导致不稳定的行为、更差的性能,以及带来移植性问题。不要把终结函数当做C++中的析构函数(destructors)的对应物。
我自己总结了一下这一条的综合性结论是这样的:
1)在涉及使用资源,使用完毕后要释放资源的情形下,首先要用一个显示的方