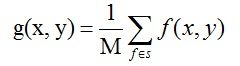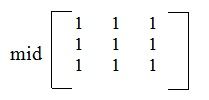图像噪声的抑制——均值滤波、中值滤波、对称均值滤波
图像噪声的抑制——均值滤波、中值滤波、对称均值滤波
分类： 图像处理
2012-11-05 19:05
837人阅读
评论(0)
收藏
举报
目录(?)[+]
概述
噪声对图像处理的影响很大，它影响图像处理的输入、采集和处理等各个环节以及输出结果。因此，在进行其它的图像处理前，需要对图像进行去噪处理。
从统计学的观点来看，凡是统计特征不随时间变化的噪声称为平稳噪声，而统计特征随时间变化的噪声称为非平稳噪声。幅值基本相同，但是噪声出现的位置是随机的，称为椒盐噪声；如果噪声的幅值是随机的，根据幅值大小的分布，有高斯型和瑞利型两种，分别称为高斯噪声和瑞利噪声。由于去除噪声处理的原理和方法很多，这里只给出了简单的描述和我自己已实现的几种方法的java源代码。
常见的去噪处理有均值滤波，中值滤波，灰度最小方差均值滤波，K近邻平滑滤波，对称近邻均值滤波，西戈玛平滑滤波等。
均值滤波
定义
均值滤波方法是，对待处理的当前像素，选择一个模板，该模板为其邻近的若干个像素组成，用模板的均值来替代原像素的值的方法。
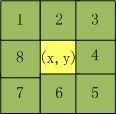
如下图，1~8为(x,y)的邻近像素。
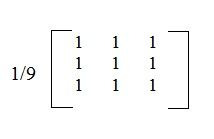
权系数矩阵模板
g = (f(x-1,y-1) + f(x,y-1)+ f(x+1,y-1) + f(x-1,y) + f(x,y) + f(x+1,y) + f(x-1,y+1) + f(x,y+1) + f(x+1,y+1))/9
方法优缺点
优点：算法简单，计算速度快；
缺点：降低噪声的同时使图像产生模糊，特别是景物的边缘和细节部分。
源代码
- /**
- * 均值滤波
- * @param srcPath 图片的存储位置
- * @param destPath 图像要保存的存储位置
- * @param format 图像要保存的存储位置
- */
- public static void avrFiltering(String srcPath,String destPath, String format) {
- BufferedImage img = readImg(srcPath);
- int w = img.getWidth();
- int h = img.getHeight();
- int[] pix = new int[w*h];
- img.getRGB(0, 0, w, h, pix, 0, w);
- int newpix[] = avrFiltering(pix, w, h);
- img.setRGB(0, 0, w, h, newpix, 0, w);
- writeImg(img, format, destPath);
- }
- /**
- * 均值滤波
- * @param pix 像素矩阵数组
- * @param w 矩阵的宽
- * @param h 矩阵的高
- * @return 处理后的数组
- */
- public static int[] avrFiltering(int pix[], int w, int h) {
- int newpix[] = new int[w*h];
- ColorModel cm = ColorModel.getRGBdefault();
- int r=0;
- for(int y=0; y<h; y++) {
- for(int x=0; x<w; x++) {
- if(x!=0 && x!=w-1 && y!=0 && y!=h-1) {
- //g = (f(x-1,y-1) + f(x,y-1)+ f(x+1,y-1)
- // + f(x-1,y) + f(x,y) + f(x+1,y)
- // + f(x-1,y+1) + f(x,y+1) + f(x+1,y+1))/9
- r = (cm.getRed(pix[x-1+(y-1)*w]) + cm.getRed(pix[x+(y-1)*w])+ cm.getRed(pix[x+1+(y-1)*w])
- + cm.getRed(pix[x-1+(y)*w]) + cm.getRed(pix[x+(y)*w]) + cm.getRed(pix[x+1+(y)*w])
- + cm.getRed(pix[x-1+(y+1)*w]) + cm.getRed(pix[x+(y+1)*w]) + cm.getRed(pix[x+1+(y+1)*w]))/9;
- newpix[y*w+x] = 255<<24 | r<<16 | r<<8 |r;
- } else {
- newpix[y*w+x] = pix[y*w+x];
- }
- }
- }
- return newpix;
- }
中值滤波
定义
中值滤波方法是，对待处理的当前像素，选择一个模板，该模板为其邻近的若干个像素组成，对模板的像素由小到大进行排序，再用模板的中值来替代原像素的值的方法。
权系数矩阵模板
g = median[(x-1,y-1) + f(x,y-1)+ f(x+1,y-1) + f(x-1,y) + f(x,y) + f(x+1,y) + f(x-1,y+1) + f(x,y+1) + f(x+1,y+1)]
优缺点
优点：抑制效果很好，画面的清析度基本保持；
缺点：对高斯噪声的抑制效果不是很好。
源代码
- /**
- * 中值滤波
- * @param srcPath 图片的存储位置
- * @param destPath 图像要保存的存储位置
- * @param format 图像要保存的存储位置
- */
- public static void medianFiltering(String srcPath, String destPath, String format) {
- BufferedImage img = readImg(srcPath);
- int w = img.getWidth();
- int h = img.getHeight();
- int[] pix = new int[w*h];
- img.getRGB(0, 0, w, h, pix, 0, w);
- int newpix[] = medianFiltering(pix, w, h);
- img.setRGB(0, 0, w, h, newpix, 0, w);
- writeImg(img, format, destPath);
- }
- /**
- * 中值滤波
- * @param pix 像素矩阵数组
- * @param w 矩阵的宽
- * @param h 矩阵的高
- * @return 处理后的数组
- */
- public static int[] medianFiltering(int pix[], int w, int h) {
- int newpix[] = new int[w*h];
- int[] temp = new int[9];
- ColorModel cm = ColorModel.getRGBdefault();
- int r=0;
- for(int y=0; y<h; y++) {
- for(int x=0; x<w; x++) {
- if(x!=0 && x!=w-1 && y!=0 && y!=h-1) {
- //g = median[(x-1,y-1) + f(x,y-1)+ f(x+1,y-1)
- // + f(x-1,y) + f(x,y) + f(x+1,y)
- // + f(x-1,y+1) + f(x,y+1) + f(x+1,y+1)]
- temp[0] = cm.getRed(pix[x-1+(y-1)*w]);
- temp[1] = cm.getRed(pix[x+(y-1)*w]);
- temp[2] = cm.getRed(pix[x+1+(y-1)*w]);
- temp[3] = cm.getRed(pix[x-1+(y)*w]);
- temp[4] = cm.getRed(pix[x+(y)*w]);
- temp[5] = cm.getRed(pix[x+1+(y)*w]);
- temp[6] = cm.getRed(pix[x-1+(y+1)*w]);
- temp[7] = cm.getRed(pix[x+(y+1)*w]);
- temp[8] = cm.getRed(pix[x+1+(y+1)*w]);
- Arrays.sort(temp);
- r = temp[4];
- newpix[y*w+x] = 255<<24 | r<<16 | r<<8 |r;
- } else {
- newpix[y*w+x] = pix[y*w+x];
- }
- }
- }
- return newpix;
- }
对称近邻均值滤波
定义
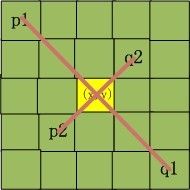
对称近邻（SNN：Symmetric Nearest Neighbor）均值滤波的核心思想是，在一个局部范围内，通过几对对称点像素的比较，获得相对区域及不同区域的差别，然后将均值计算在所判定的同一个区域内进行，这样可以使边界的保持更加灵活的同时又降低计算。
设一个(2N+1)*(2N+1)的模板，则有2N*(2N+1)个对称点，2N*(2N+1)个选择点的像素均值代替原像素值，如下：
优缺点
使边界的保持更加灵活的同时又降低计算。
源代码
- /**
- * 对称近邻均值滤波
- * @param srcPath 图片的存储位置
- * @param destPath 图像要保存的存储位置
- * @param format 图像要保存的存储位置
- */
- public static void snnFiltering(String srcPath, String destPath, String format) {
- BufferedImage img = readImg(srcPath);
- int w = img.getWidth();
- int h = img.getHeight();
- int[] pix = new int[w*h];
- img.getRGB(0, 0, w, h, pix, 0, w);
- int newpix[] = snnFiltering(pix, w, h);
- img.setRGB(0, 0, w, h, newpix, 0, w);
- writeImg(img, format, destPath);
- }
- /**
- * 对称近邻均值滤波
- * @param pix 像素矩阵数组
- * @param w 矩阵的宽
- * @param h 矩阵的高
- * @return 处理后的数组
- */
- public static int[] snnFiltering(int pix[], int w, int h) {
- int newpix[] = new int[w*h];
- int n = 9;
- int temp, i1,i2, sum;
- int[] temp1 = new int[n];
- int[] temp2 = new int[n/2];
- ColorModel cm = ColorModel.getRGBdefault();
- int r=0;
- for(int y=0; y<h; y++) {
- for(int x=0; x<w; x++) {
- if(x!=0 && x!=w-1 && y!=0 && y!=h-1) {
- sum = 0;
- temp1[0] = cm.getRed(pix[x-1+(y-1)*w]);
- temp1[1] = cm.getRed(pix[x+(y-1)*w]);
- temp1[2] = cm.getRed(pix[x+1+(y-1)*w]);
- temp1[3] = cm.getRed(pix[x-1+(y)*w]);
- temp1[4] = cm.getRed(pix[x+(y)*w]);
- temp1[5] = cm.getRed(pix[x+1+(y)*w]);
- temp1[6] = cm.getRed(pix[x-1+(y+1)*w]);
- temp1[7] = cm.getRed(pix[x+(y+1)*w]);
- temp1[8] = cm.getRed(pix[x+1+(y+1)*w]);
- for(int k=0; k<n/2; k++) {
- i1 = Math.abs(temp1[n/2] - temp1[k]);
- i2 = Math.abs(temp1[n/2] - temp1[n-k-1]);
- temp2[k] = i1<i2 ? temp1[k] : temp1[n-k-1]; //选择最接近原像素值的一个邻近像素
- sum = sum + temp2[k];
- }
- r = sum/(n/2);
- //System.out.println("pix:" + temp1[4] + " r:" + r);
- newpix[y*w+x] = 255<<24 | r<<16 | r<<8 |r;
- } else {
- newpix[y*w+x] = pix[y*w+x];
- }
- }
- }
- return newpix;
- }