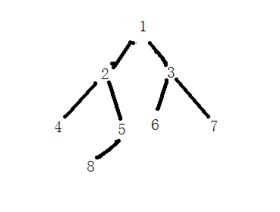
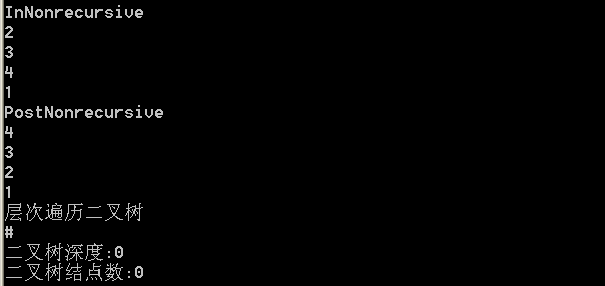基本二叉树操作
涉及的内容包括递归前序,中序和后序遍历;非递归前中后序遍历;二叉树的层次遍历;求二叉树的深度;求二叉树的结点数。
其中二叉树的非递归遍历都是用的C++中的stack和set容器,方法比较笨(同时想到的另一个方法是修改二叉树的数据结构,在节点的结构体中增加一个标志位,在遍历的时候当节点输出后设置标志位为访问过,其效果与利用set容器一样,但相对方便些)。二叉树的层次遍历用到了vector可自增长的特性,而且使用下标取值的方法,而用迭代器iterator就会出现问题,因为push_back()操作之后原来容器中的迭代器就会失效。求二叉树深度和结点数的程序都是用到了递归的方法。
创建二叉树是用的先序遍历次序的方法,其中空结点用字符'#'来表示,而这种标记方法也给后来其他二叉树的操作带来了方便,主要是可以确定一些循环的结束条件。在创建二叉树的时候需要为新的结点提前申请好空间否则就会将指针指向NULL。
#include <iostream>
#include <stack>
#include <vector>
#include <set>
using namespace std;
typedef struct TreeNode
{
char data;
struct TreeNode *lchild;
struct TreeNode *rchild;
}TreeNode, *pTreeNode; //
// 创建二叉树(先序)
//pTreeNode CreateBinaryTree(pTreeNode root)
int CreateBinaryTree(pTreeNode root)
{
char ch;
//TreeNode root;
cout<<"Please input the node:"<<endl;
//root=new TreeNode;
cin>>ch;
if(ch=='#')
//return root->data=ch;
{
root->data=ch;
//return root;
return 0;
}
else
{
root->data=ch;
CreateBinaryTree(root->lchild=new TreeNode);
CreateBinaryTree(root->rchild=new TreeNode);
}
//return root;
return 0;
}
// 先序递归遍历
int PreOrderTraverse(pTreeNode root)
{
if(root->data=='#')
return 0;
cout<<root->data<<endl;
PreOrderTraverse(root->lchild);
PreOrderTraverse(root->rchild);
return 0;
}
// 中序递归遍历
int InOrderTraverse(pTreeNode root)
{
if(root->data=='#')
return 0;
InOrderTraverse(root->lchild);
cout<<root->data<<endl;
InOrderTraverse(root->rchild);
return 0;
}
// 后序递归遍历
int PostOrderTraverse(pTreeNode root)
{
if(root->data=='#')
return 0;
PostOrderTraverse(root->lchild);
PostOrderTraverse(root->rchild);
cout<<root->data<<endl;
return 0;
}
// 前序非递归遍历
int PreNonrecursive(pTreeNode root)
{
stack<pTreeNode> S;
set<int> Array;
S.push(root);
cout<<S.top()->data<<endl;
Array.insert(S.top()->data);
//while(!S.empty())
for(;;)
{
if(root->lchild->data!='#' && Array.find(root->lchild->data)==Array.end())
{
S.push(root->lchild);
Array.insert(S.top()->data);
cout<<S.top()->data<<endl;
root=root->lchild; //
}
else if(root->rchild->data!='#' && Array.find(root->rchild->data)==Array.end())
{
S.push(root->rchild);
Array.insert(S.top()->data);
cout<<S.top()->data<<endl;
root=root->rchild;
}
else
{
S.pop();
//if(S.top()==NULL)
// break;
//else
if(S.empty())
break;
else
root=S.top();
}
}
return 0;
}
// 中序非递归遍历
int InNonrecursive(pTreeNode root)
{
stack<pTreeNode> S;
set<int> Array;
S.push(root);
for(;;)
{
if(root->lchild->data!='#' && Array.find(root->lchild->data)==Array.end())
{
S.push(root->lchild);
root=root->lchild;
}
else
{
if(Array.find(root->data)==Array.end())
{
cout<<S.top()->data<<endl;
Array.insert(S.top()->data);
}
if(root->rchild->data!='#' && Array.find(root->rchild->data)==Array.end())
{
S.push(root->rchild);
root=root->rchild;
}
else
{
S.pop();
if(S.empty())
break;
root=S.top();
}
}
}
return 0;
}
// 后序非递归遍历
int PostNonrecursive(pTreeNode root)
{
stack<pTreeNode> S;
set<int> Array;
S.push(root);
for(;;)
{
if(root->lchild->data!='#' && Array.find(root->lchild->data)==Array.end())
{
S.push(root->lchild);
root=root->lchild; //
}
else
{
if(root->rchild->data!='#' && Array.find(root->rchild->data)==Array.end())
{
S.push(root->rchild);
root=root->rchild;
}
else
{
cout<<S.top()->data<<endl;
Array.insert(S.top()->data);
S.pop();
if(S.empty())
break;
root=S.top();
}
}
}
return 0;
}
int HierarchicalTraverse(pTreeNode root)
{
int i=0;
vector<pTreeNode> V;
V.push_back(root);
for(;;)
{
if(V[i]->lchild->data!='#')
V.push_back(V[i]->lchild);
if(V[i]->rchild->data!='#')
V.push_back(V[i]->rchild);
i++;
if(i==V.end()-V.begin()) // 通过标识将迭代器转化为下标
break;
}
vector<pTreeNode>::iterator j;
for(j=V.begin();j!=V.end();j++)
cout<<(*j)->data<<endl;
return 0;
}
/*
int HierarchicalTraverse(pTreeNode root)
{
vector<pTreeNode> V;
V.push_back(root);
vector<pTreeNode>::iterator i=V.begin();
for(;;)
{
if((*i)->lchild->data!='#')
V.push_back((*i)->lchild); 任何改变vector长度的操作都会使已存在的迭代器失效。
例如,在调用push_back之后,就不能再信赖指向vector的迭代器的值了。
if((*i)->rchild->data!='#')
V.push_back((*i)->rchild);
i++;
if(i==V.end())
break;
}
for(i=V.begin();i!=V.end();i++)
cout<<(*i)->data<<endl;
return 0;
}
*/
int TreeDepth(pTreeNode root)
{
int depth=0;
if(root->data=='#')
return depth;
if(root->lchild->data=='#' && root->rchild->data=='#')
depth=1;
else
{
int l=TreeDepth(root->lchild);
int r=TreeDepth(root->rchild);
depth=1+(l>r?l:r); // ?:运算符优先级最低
}
return depth;
}
int NodeCounts(pTreeNode root)
{
int count=0;
if(root->data=='#')
return count;
if(root->lchild->data=='#' && root->rchild->data=='#')
count=1;
else
count=count+NodeCounts(root->lchild)+NodeCounts(root->rchild)+1;
return count;
}
int main()
{
pTreeNode r=new TreeNode;
//r=CreateBinaryTree(r);
CreateBinaryTree(r);
cout<<"After Creation:"<<endl;
cout<<"PreOrderTraverse:"<<endl;
PreOrderTraverse(r);
cout<<"InOrderTraverse:"<<endl;
InOrderTraverse(r);
cout<<"PostOrderTraverse:"<<endl;
PostOrderTraverse(r);
cout<<"PreNonrecursive"<<endl;
PreNonrecursive(r);
cout<<"InNonrecursive"<<endl;
InNonrecursive(r);
cout<<"PostNonrecursive"<<endl;
PostNonrecursive(r);
cout<<"层次遍历二叉树"<<endl;
HierarchicalTraverse(r);
cout<<"二叉树深度:"<<TreeDepth(r)<<endl;
cout<<"二叉树结点数:"<<NodeCounts(r)<<endl;
return 0;
}
所需要的输入为:124##58###36##7##
部分结果为:
参考了一下别人的代码,重新做了一下二叉树的先序和中序遍历,其没有用到set容器来保存已经遍历过的结点值,而是直接在遍历过程中将遍历过的节点出栈,更好地实现了迭代的方法,其对栈有一部分的操作开始还以为是写错了,后来才明白了其中的含义,中序与前序的思路基本一样,后序稍微有些复杂需要保存之前的变量,代码如下:
// 前序非递归遍历 (将输出结点值后的结点出栈)
int PreNonrecursive(pTreeNode root)
{
stack<pTreeNode> S;
pTreeNode p=root;
S.push(p);
cout<<p->data<<endl;
p=p->lchild;
while(!S.empty() || p->data!='#') // 条件判断处需注意,因在根节点处遍历完根节点后根节点出栈则栈为空,但此时还有右孩子非空等待入栈
{
if(p->data!='#')
{
S.push(p);
cout<<p->data<<endl;
p=p->lchild;
}
else
{
p=S.top();
p=p->rchild;
S.pop();
}
}
return 0;
} 相比于前序非递归遍历,中序遍历只是改变了输出节点语句的位置。
// 中序非递归遍历
int InNonrecursive(pTreeNode root)
{
stack<pTreeNode> S;
pTreeNode p=root;
S.push(p);
p=p->lchild;
while(!S.empty() || p->data!='#')
{
if(p->data!='#')
{
S.push(p);
p=p->lchild;
}
else
{
p=S.top();
cout<<p->data<<endl;
p=p->rchild;
S.pop();
}
}
return 0;
}
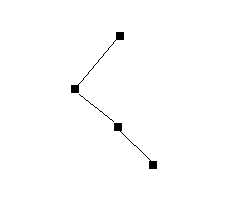
后序遍历中,我开始也是模仿前序和中序遍历的方式,然后在结合后序遍历的特点做一下修正,用到的方法就是给出一些二叉树的特殊的情况,比如如下的形式:
然后不断地调整代码的写法,暂时还没找到一个想法可以很清晰地说明代码就该这么写,在写的时候只知道有两点可以利用:1,满足二叉树后序遍历的规则,也就是左右根的顺序。2,可以利用栈的操作来完成回溯。
在先序和中序遍历中,可以在遍历完节点后直接处理节点,而在后序遍历中却需要保存节点,直到符合要求的时候才做处理(主要是pop()操作),为保存父子节点我定义了两个指针,但是按照原来的想法还是不能够完成后序遍历,因为按照原来的操作在回溯后无法判断此节点右子树是否遍历过,则会造成死循环,为此需要有一个标志位来表明此右孩子已经遍历过,这就涉及到最开始用到的两个想法:1,利用set容器保存已遍历节点的值。2,修改数据结构设置标志位字段。但是想摆脱这样的算法又该如何呢?
后来我还是看了上篇的文章,但是联系到自己设置的数据结构则会修改已经建立好的树,其思想是:将遍历过的节点置为空,在本文中即node->data='#'。这样在条件判断时就可以加上一句判断是否遍历过的语句。但是这样就完全破坏了树的结构,让后续的操作无法进行,虽然可以正确的得到后序遍历的结果。代码如下:这一部分写错了,是将遍历过的节点用另一个指向节点的指针记录下来,然后在回溯的时候可以判断回溯节点的右子树是否已经遍历过。(其实置空也是可以的,不过破坏了树结构,如下)
int PostNonrecursive(pTreeNode root)
{
stack<pTreeNode> S;
pTreeNode p=root, q=NULL;
S.push(p);
p=p->lchild;
while(!S.empty())
{
if(p->data!='#')
{
S.push(p);
q=p; // q记录上一个节点
p=p->lchild;
}
else
{
p=q->rchild;
if(p->data=='#')
{
cout<<q->data<<endl;
q->data='#'; // 只增加这一句便可完成置为空的操作
S.pop();
if(!S.empty())
q=S.top();
else
break;
}
}
}
return 0;
}会出现如下的错误:
树的结构被破坏。
但是在参考文章中同样的思想却可以顺利地进行其余的操作,这究竟是为什么呢?原来在建立和遍历树的时候,作者用到了不同的数据结构。用的是相同的结构,是算法不同。
int PostNonrecursive(pTreeNode root)
{
stack<pTreeNode> S;
pTreeNode p=root, q=NULL;
S.push(p);
p=p->lchild;
while(!S.empty())
{
if(p->data!='#')
{
S.push(p);
p=p->lchild;
}
else
{
p=S.top();
if(p->rchild->data=='#' || p->rchild==q)
{
cout<<p->data<<endl;
q=p; // 记录遍历后的节点
S.pop();
p=new TreeNode; // 因为在树的节点建立过程中是利用 '#'来表示空,但是不能在原节点上操作,故新建节点
p->data='#'; // 主要的目的是避免重复入栈操作
}
else
p=p->rchild;
}
}
return 0;
}
可以在建树的时候,将代码:
if(ch=='#')
{
root->data=ch;
return 0;
}
改为
if(ch=='#')
{
root=NULL;
return 0;
}
此时其他的代码也需要修改,这样所有的判断空节点的语句 p->data=='#'就将改为p==NULL,这样更符合平常的习惯。上文写错了,犯了最基本的错误----函数传参赋值的错误,因为CreateBinaryTree()的参数是pTreeNode类型(指针类型),在函数中直接修改参数的值是没有用处的,因为在函数内部用了一个在栈中的临时变量代替参数,函数结束后变量释放,参数值是没有被修改的,所以为了达到目的需要传递参数的地址,在这里就是指针的地址,也就是指向指针的指针,这样才能满足为指针符空值,修改如下:
// 创建二叉树(先序)
//pTreeNode CreateBinaryTree(pTreeNode root)
int CreateBinaryTree(pTreeNode *root)
{
char ch;
//TreeNode root;
cout<<"Please input the node:"<<endl;
//root=new TreeNode;
cin>>ch;
if(ch=='#')
//return root->data=ch;
{
*root=NULL;
//return root;
return 0;
}
else
{
(*root)->data=ch;
CreateBinaryTree(&((*root)->lchild=new TreeNode));
CreateBinaryTree(&((*root)->rchild=new TreeNode));
}
//return root;
return 0;
}其他函数不需要做改正,只是在需要判断空节点的时候将p->data=='#'改为p==NULL即可,修改后序遍历为:
int PostNonrecursive(pTreeNode root)
{
stack<pTreeNode> S;
pTreeNode p=root, q=NULL;
S.push(p);
p=p->lchild;
while(!S.empty())
{
if(p != NULL)
{
S.push(p);
p=p->lchild;
}
else
{
p=S.top();
if(p->rchild == NULL || p->rchild==q)
{
cout<<p->data<<endl;
q=p;
S.pop();
p=NULL;
}
else
p=p->rchild;
}
}
return 0;
}