BNUOJ 51277 魔方复原(模拟、置换)
题意:
给定N≤105的三阶魔方操作序列
由U、D、R、L、F、B操作构成,如下图:
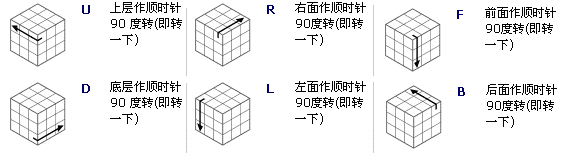
操作序列表示如下,R≤109:
1.可以是任何一个只由大写字母U、D、R、L、F、B组成的字符串
2.可以被表示为另一个字符串重复多次的形式。具体来说,S可以被表示为“R(S1)”这样的形式,用来表示S1被连续重复R次
3.可以被表示成一些字符串首尾相连的形式。具体来说,S可以被表示为“S1S2...Sk”这样的形式,表示S1、S2、...、Sk这些字符串首尾相连
4.一个空字符串(“”)也是一种合法的形式
求出这个操作序列重复多少次之后魔方会第一次恢复到初始状态
分析:
对魔方的每个方块标号之后,每个操作的置换可以手工推出
由于多次操作的复合仍然是一个置换,因此魔方总是能复原,并且将置换分解成环之后,ans=这些环长度的lcm
现在考虑如何处理操作序列:
1.对于只包含字母的序列,直接模拟即可
2.对于需要将某一段重复多次的序列,只需对处理循环节之后得到的置换做一个若干次幂,快速幂即可
3.对于括号嵌套的情况,直接递归处理即可
可以如上处理的原因是置换满足结合律
代码:
//
// Created by TaoSama on 2016-02-05
// Copyright (c) 2016 TaoSama. All rights reserved.
//
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <set>
#include <vector>
using namespace std;
#define pr(x) cout << #x << " = " << x << " "
#define prln(x) cout << #x << " = " << x << endl
const int N = 1e5 + 10, INF = 0x3f3f3f3f, MOD = 1e9 + 7;
const int L = 54;
const char op[7]="FLRUDB";
const int d[6][5][4]=
{
{{1,3,9,7},{2,6,8,4},{43,19,48,18},{44,22,47,15},{45,25,46,12}},//F
{{10,12,18,16},{11,15,17,13},{37,1,46,36},{40,4,49,33},{43,7,52,30}},//L
{{19,21,27,25},{20,24,26,22},{54,9,45,28},{51,6,42,31},{48,3,39,34}},//R
{{37,39,45,43},{38,42,44,40},{28,19,1,10},{29,20,2,11},{30,21,3,12}},//U
{{16,7,25,34},{17,8,26,35},{46,48,54,52},{47,51,53,49},{18,9,27,36}},//D
{{28,30,36,34},{29,33,35,31},{27,39,10,52},{24,38,13,53},{21,37,16,54}}//B
};
void trans(vector<int>& p, int o){
for(int i = 0; i < 5; ++i){
int t = p[d[o][i][3]];
for(int j = 3; j; --j)
p[d[o][i][j]] = p[d[o][i][j - 1]];
p[d[o][i][0]] = t;
}
}
void multiply(vector<int>& p, vector<int>& q){
vector<int> t(L + 1);
for(int i = 1; i <= L; ++i) t[i] = p[q[i]];
p = t;
}
char s[N];
int idx;
vector<int> dfs(){
vector<int> p(L + 1);
for(int i = 1; i <= L; ++i) p[i] = i;
while(s[idx] && s[idx] != ')'){
if(isdigit(s[idx])){
int r = 0;
while(isdigit(s[idx])) r = r * 10 + s[idx++] - '0';
++idx; //(
vector<int> q = dfs();
for(; r; r >>= 1){
if(r & 1) multiply(p, q);
multiply(q, q);
}
}
else trans(p, strchr(op, s[idx++]) - op);
}
++idx; //)
return p;
}
int main() {
#ifdef LOCAL
freopen("C:\\Users\\TaoSama\\Desktop\\in.txt", "r", stdin);
// freopen("C:\\Users\\TaoSama\\Desktop\\out.txt","w",stdout);
#endif
ios_base::sync_with_stdio(0);
int t; scanf("%d", &t);
while(t--){
scanf("%s", s);
idx = 0;
vector<int> p = dfs();
int ans = 1; bool vis[L + 1] = {};
for(int i = 1; i <= L; ++i){
if(vis[i]) continue;
int cycle = 0, tmp = i;
do{
++cycle;
vis[tmp] = true;
tmp = p[tmp];
}while(tmp != i);
ans = ans / __gcd(ans, cycle) * cycle;
}
printf("%d\n", ans);
}
return 0;
}