伸展树的读书笔记

         最近开始了自己高级数据结构之旅，在这次旅行中，我将持续把一些高级的数据结构从理论到编码都过一遍，同时通过博客形式分享出来，希望大家指出不足之处！

       二叉排序树是一种动态排序的数据结构，支持插入、删除、查找等操作，且平均时间复杂度为O(log(N))，但是普通二叉排序树不能保证树退化为一颗分支的情况，此时最坏情况下的时间复杂度为O（N）。此时，平衡二叉树的产生了。平衡二叉树是一种动态调整平衡的数据结构，但理想的平衡二叉树很难，于是人们使用AVL、红黑树、Treap、伸展树等来替代平衡二叉树，这些数据结构可以很好地改善最坏情况。但实现起来并不是很容易的事。

        伸展树较其他的数据结构，有着明显的特点。与纯的二叉查找树比起来，伸展树的查找、插入、删除等操作的平摊时间复杂度O(log(N))，且与AVL、红黑树比起来实现简单、空间效率高。关于伸展树的具体原理，可以参考算法合集之《伸展树的基本操作与应用》，这是国家队大牛写的，可读性很强。

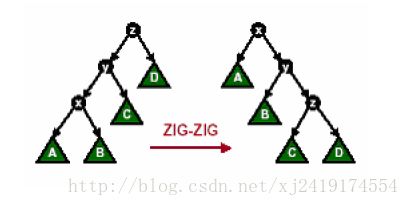
       伸展树的基本原理是80—20原则，学计算机的人对这个原则的内容肯定不陌生：计算机80%的数据访问在集中在20%的数据上，如存储器中的Cache就是用的这个原理，并且效果很不错。伸展树正是利用这样的设计思想来进行的，将当前操作的数据通过伸展操作移到根节点，在这个过程中保持二叉查找树的性质，从而是整个过程的平摊时间复杂度降到O(log(N))。当然，对于单个操作，时间复杂度可能到达O(N)，但基于整体考虑以及计算机特定规律，伸展树还是有着很好的效率的。在伸展的过程中，主要涉及两个旋转操作，左旋或右旋。在设计算法时，我们通常将时间复杂度放在首位，这点无可厚非，但有时我们的结合具体题目要求，在时间复杂度、空间复杂度、编程实现难度间寻找平衡，于是伸展树被认为是拥有很重要现实价值的”平衡二叉树“。

                         

                                                      

      上面从左到右为右旋，从右到左为左旋，其他所有操作都是由这两种基本操作组合起来的。如下

       以上3副图包含了伸展树所有的Splay操作，而基本的左旋右选得到。

      普通伸展树支持插入、删除、修改、查询等操作。关于伸展树，有自顶向下和自底向上两种实现方法，这里我选用的是自底向上的实现方法，由于在节点中有父节点，故不用记录路径。

下面贴上我的代码：

//伸展树节点头文件SplayTreeNode.h

#include<iostream>
using namespace std;

/**********************************
*功能:防止头文件多次包含
**********************************/
#ifndef SPLAYTREENODE_H
#define SPLAYTREENODE_H

class SplayTreeNode
{
public:
	SplayTreeNode *leftChild;
	SplayTreeNode *rightChild;
	SplayTreeNode *parent;
	int key;
	SplayTreeNode(int key)
	{
		this->key=key;
		this->leftChild=NULL;
		this->rightChild=NULL;
		this->parent=NULL;
	}
};

#endif SPLAYTREENODE_H

 

//伸展树源文件SplayTree.cpp

#include<iostream>
#include"SplayTreeNode.h"
using namespace std;

class SplayTree
{
private:
	SplayTreeNode *root;
	void LeftRotate(SplayTreeNode *);
	void RightRotate(SplayTreeNode *);
	void Splay(SplayTreeNode *);
	void PreOrderSTPrint(SplayTreeNode *);
	void InOrderSTPrint(SplayTreeNode *);
	void RotateSTPrint(SplayTreeNode *,int);
	void SufOrderSTPrint(SplayTreeNode *);
	void DeleteNoOrOneChildSTNode(SplayTreeNode *,SplayTreeNode *);
public:
	SplayTree();
	void InsertSplayTree(int);
	bool DeleteSplayTree(int);
	bool UpdataSplayTree(int,int);
	SplayTreeNode *FindSplayTree(int);
	void PreOrderSTPrint();
	void InOrderSTPrint();
	void RotateSTPrint();
	void SufOrderSTPrint();
};

SplayTree::SplayTree()
{
	this->root=NULL;
} 

/**************************************************************
*参数：待左旋的节点
*返回值：空
*功能：左旋
***************************************************************/
void SplayTree::LeftRotate(SplayTreeNode *tempSTNode)
{
	SplayTreeNode *rChild=tempSTNode->rightChild;
	if(NULL!=tempSTNode->parent)//不为根节点
	{
		if(tempSTNode->parent->leftChild==tempSTNode)
			tempSTNode->parent->leftChild=rChild;
		else 
			tempSTNode->parent->rightChild=rChild;
	}
	rChild->parent=tempSTNode->parent;
	tempSTNode->parent=rChild;
	if(rChild->leftChild!=NULL)
		rChild->leftChild->parent=tempSTNode;
	tempSTNode->rightChild=rChild->leftChild;
	rChild->leftChild=tempSTNode;
	if(NULL==rChild->parent)
		this->root=rChild;
}

/**************************************************************
*参数：待右旋的节点
*返回值：空
*功能：右旋
***************************************************************/
void SplayTree::RightRotate(SplayTreeNode *tempSTNode)
{
	SplayTreeNode *lChild=tempSTNode->leftChild;
	if(NULL!=tempSTNode->parent)//不为根节点
	{
		if(tempSTNode->parent->rightChild==tempSTNode)
			tempSTNode->parent->rightChild=lChild;
		else 
			tempSTNode->parent->leftChild=lChild;
	}
	lChild->parent=tempSTNode->parent;
	tempSTNode->parent=lChild;
	if(lChild->rightChild!=NULL)
		lChild->rightChild->parent=tempSTNode;
	tempSTNode->leftChild=lChild->rightChild;
	lChild->rightChild=tempSTNode;
	if(NULL==lChild->parent)
		this->root=lChild;
}

/**************************************************************
*参数：待伸展的节点
*返回值：空
*功能：将当前节点伸展的根节点
***************************************************************/
void SplayTree::Splay(SplayTreeNode *tempSTNode)
{
	while(NULL!=tempSTNode&&NULL!=tempSTNode->parent)
	{
		if(tempSTNode->parent->leftChild==tempSTNode)//父亲节点右旋
			RightRotate(tempSTNode->parent);
		else LeftRotate(tempSTNode->parent);
	}
}

/**************************************************************
*参数：带插入元素
*返回值：空
*功能：将当前元素插入伸展树
***************************************************************/
void SplayTree::InsertSplayTree(int tempKey)
{
	SplayTreeNode *pre=NULL,*cur=this->root;
	while(cur!=NULL)
	{
		pre=cur;
		if(cur->key>tempKey)//tempKey插到左子树
			cur=cur->leftChild;
		else cur=cur->rightChild;//插到左子树
	}
	SplayTreeNode *tempSTNode=new SplayTreeNode(tempKey);
	tempSTNode->parent=pre;
	if(pre==NULL)//若插入的为根节点
	{
		this->root=tempSTNode;
	}
	else if(pre->key>tempSTNode->key)
		pre->leftChild=tempSTNode;
	else pre->rightChild=tempSTNode;
	Splay(tempSTNode);
}

/**************************************************************
*参数：带查找元素
*返回值：返回查找元素在伸展树中的位置
*功能：查找当前元素是否在伸展树
***************************************************************/
SplayTreeNode *SplayTree::FindSplayTree(int tempKey)
{
	SplayTreeNode *cur=this->root;
	while(cur!=NULL)
	{
		if(cur->key==tempKey)
			break;
		else if(cur->key>tempKey)
			cur=cur->leftChild;
		else cur=cur->rightChild;
	}
	Splay(cur);
	return cur;
}

/**********************************************************
*参数：pre待删除节点的父节点，cur待删除节点
*返回值：空
*功能：删除左右孩子有为空的情况
************************************************************/
void SplayTree::DeleteNoOrOneChildSTNode(SplayTreeNode *pre,SplayTreeNode *cur)
{
	if(NULL==cur->leftChild&&NULL==cur->rightChild)//左右孩子为空
	{
		if(NULL==pre)
			this->root=NULL;
		else if(pre->leftChild==cur)
			pre->leftChild=NULL;
		else pre->rightChild=NULL;
		delete cur;
	}
	else if(cur->rightChild!=NULL)//若右子树不为空
	{
		if(NULL==pre)
		{
			this->root=cur->rightChild;
			cur->rightChild->parent=NULL;
		}
		else if(pre->leftChild==cur)
		{
			pre->leftChild=cur->rightChild;
			cur->rightChild->parent=pre;
		}
		else 
		{
			pre->rightChild=cur->rightChild;
			cur->rightChild->parent=pre;
		}
		delete cur;
	}
	else if(cur->leftChild!=NULL)//若左子树不为空
	{
		if(NULL==pre)
		{
			this->root=cur->leftChild;
			cur->leftChild->parent=NULL;
		}
		else if(pre->leftChild==cur)
		{
			pre->leftChild=cur->leftChild;
			cur->leftChild->parent=pre;
		}
		else
		{
			pre->rightChild=cur->leftChild;
			cur->leftChild->parent=pre;
		}
		delete cur;
	}
}


/**********************************************************
*参数：待删除节点元素
*返回值：空
*功能：删除元素主函数
************************************************************/
bool SplayTree::DeleteSplayTree(int tempKey)
{
	SplayTreeNode *pre=NULL,*cur=root;
	while(cur!=NULL)//寻找待删除元素
	{
		if(cur->key==tempKey)
			break;
		else
		{
			pre=cur;
			if(cur->key>tempKey)
				cur=cur->leftChild;
			else cur=cur->rightChild;
		}
	}
	if(NULL==cur)return false;
	if(NULL==cur->leftChild||NULL==cur->rightChild)
	{
		DeleteNoOrOneChildSTNode(pre,cur);
		Splay(pre);
	}
	else //左右子树都不为空
	{
		SplayTreeNode *rPre=cur,*rCur=cur->rightChild;//找到右子树最小元素
		while(rCur->leftChild!=NULL)
		{
			rPre=rCur;
			rCur=rCur->leftChild;
		}
		cur->key=rCur->key;
		DeleteNoOrOneChildSTNode(rPre,rCur);
		Splay(rPre);
	}
	return true;
}

/**********************************************************
*参数：待修改节点元素、修改后的元素
*返回值：返回修改是否成功
*功能：修改函数
************************************************************/
bool SplayTree::UpdataSplayTree(int oldKey,int newKey)
{
	if(DeleteSplayTree(oldKey))
	{
		InsertSplayTree(newKey);
		return true;
	}
	return false;
}

/**********************************************************
*参数：当前子树根节点
*返回值：空
*功能：前序遍历二叉查找树
************************************************************/
void SplayTree::PreOrderSTPrint(SplayTreeNode *tempSTNode)
{
	if(NULL==tempSTNode)
		return ;
	cout<<tempSTNode->key<<"    ";
	PreOrderSTPrint(tempSTNode->leftChild);
	PreOrderSTPrint(tempSTNode->rightChild);
}
void SplayTree::PreOrderSTPrint()
{
	PreOrderSTPrint(this->root);
}

/**********************************************************
*参数：当前子树根节点
*返回值：空
*功能：中序遍历二叉查找树
************************************************************/
void SplayTree::InOrderSTPrint(SplayTreeNode *tempSTNode)
{
	if(NULL==tempSTNode)
		return ;
	InOrderSTPrint(tempSTNode->leftChild);
	cout<<tempSTNode->key<<"   ";
	InOrderSTPrint(tempSTNode->rightChild);
}
void SplayTree::InOrderSTPrint()
{
	InOrderSTPrint(this->root);
}

/**********************************************************
*参数：当前子树根节点
*返回值：空
*功能：后序遍历二叉查找树树
************************************************************/
void SplayTree::SufOrderSTPrint(SplayTreeNode *tempSTNode)
{
	if(NULL==tempSTNode)
		return ;
	SufOrderSTPrint(tempSTNode->leftChild);
	SufOrderSTPrint(tempSTNode->rightChild);
	cout<<tempSTNode->key<<"    ";
}
void SplayTree::SufOrderSTPrint()
{
	SufOrderSTPrint(this->root);
}

/**********************************************************
*参数：当前子树根节点，缩进列数
*返回值：空
*功能：翻转打印伸展树
************************************************************/
void SplayTree::RotateSTPrint(SplayTreeNode *tempSTNode,int tempColumn)
{
	if(NULL==tempSTNode)
		return ;
	RotateSTPrint(tempSTNode->leftChild,tempColumn+1);
	for(int i=0;i<tempColumn;i++)
		cout<<"    ";
	cout<<"---"<<tempSTNode->key<<endl;
	RotateSTPrint(tempSTNode->rightChild,tempColumn+1);
}
void SplayTree::RotateSTPrint()
{
	RotateSTPrint(this->root,0);
}


void Menu()
{
	int val,choice,newVal;
	SplayTree mySplayTree;
	while(true)
	{
		do
		{
			cout<<"&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&"<<endl;
			cout<<"       1.插入"<<endl;
			cout<<"       2.删除"<<endl;
			cout<<"       3.修改"<<endl;
			cout<<"       4.查找"<<endl;
			cout<<"       5.显示"<<endl;
			cout<<"       6.返回"<<endl;
			cout<<"请输入你的选项[ ]\b\b";
			cin>>choice; 
		}while(choice!=1&&choice!=2&&choice!=3&&choice!=4&&choice!=5&&choice!=6);
		if(1==choice)
		{
			cin>>val;
			mySplayTree.InsertSplayTree(val);
		}
		else if(2==choice)
		{
			cin>>val;
			if(mySplayTree.DeleteSplayTree(val))
				cout<<"删除成功!"<<endl;
			else cout<<"删除失败!"<<endl;
		}
		else if(3==choice)
		{
			cin>>val>>newVal;
			if(mySplayTree.UpdataSplayTree(val,newVal))
				cout<<"修改成功!"<<endl;
			else cout<<"修改失败!"<<endl;
		}
		else if(4==choice)
		{
			cin>>val;
			if(NULL!=mySplayTree.FindSplayTree(val))
				cout<<"查找成功!"<<endl;
			else cout<<"查找失败!"<<endl;
		}
		else if(5==choice)
		{
			cout<<endl<<"*****************************"<<endl;
			cout<<endl<<"==========前序=============="<<endl;
			mySplayTree.PreOrderSTPrint();
			cout<<endl<<"==========中序================"<<endl;
			mySplayTree.InOrderSTPrint();
			cout<<endl<<"==========后续==============="<<endl;
			mySplayTree.SufOrderSTPrint();
			cout<<endl<<"==========对称+旋转==============="<<endl;
			mySplayTree.RotateSTPrint();
			cout<<endl<<"*****************************"<<endl;
		}
		else return ;
	}
}


int main()
{
	while(true)
		Menu();
	system("pause");
	return 0;
}

 

关于伸展树的其他操作，后续在其他博客中补上。由于时间有限，缺乏测试，可能有错，欢迎大家斧正！