如何实现具有最大值、最小值和中间值的栈和队列

在研究“如何实现具有最大值、最小值和中间值的栈和队列”前，我们先考虑以下问题，然后由此过度到题目问题。

1）如何用两个栈实现队列

2）如何用两个队列实现栈

3）如何实现包含获取最小值函数getMin()的栈

4）如何实现包含获取中间值函数getMedian()的栈

5）如何实现包含获取最小值函数getMin()的队列

1 如何用两个栈实现队列

在研究问题前，我们可以用2个栈模拟一下具体操作过程，可以总结出以下规律：

入队：元素插入stack1;

出队：如果stack2中为空，先将stack1中元素入栈stack2，然后再将stack2的栈顶元素出栈。否则直接将stack2中元素出栈。

队列为空：stack1和stack2同时为空

队列大小：为stack1和stack2大小之和

具体过程见下图（图来自《剑指offer》）

Java实现代码如下

public class QueueByStack<E extends Comparable<E>>  {
	
	private LinkedList stack1=null;
	private LinkedList stack2=null;
	
	//constructor
	public QueueByStack(){
		stack1=new LinkedList();
		stack2=new LinkedList();
	}//end QueueByStack
		
	public void insert(E e){
          stack1.addLast(e);
	}//end insert()
	
	public E remove(){
		if(!isEmpty()){
			if(stack2.isEmpty()){
				stack1Tostack2();
			}//end if

			return (E)stack2.removeLast();
		}//end if
		else{
			System.out.println("queue is empty");
			return null;
		}//end else
	}//end remove
	
	//将stack1中元素入栈stack2
	private void stack1Tostack2(){
		while(!stack1.isEmpty()){
			stack2.addLast(stack1.removeLast());
		}//end while	
	}//end stack1ToStack2()
	
	public boolean isEmpty(){
		return stack1.isEmpty() && stack2.isEmpty();
	}//end isEmpty()
	
	public int size(){
		return (stack1.size()+stack2.size());
	}//end size()

	/**
	 * @param args
	 */
	public static void main(String[] args) {
		QueueByStack q=new QueueByStack();
		q.insert(1);
		q.insert(2);
		q.insert(3);
		System.out.println(q.remove());
		System.out.println(q.remove());
		q.insert(4);
		System.out.println(q.remove());
		System.out.println(q.remove());
	}
}

2 如何用两个队列实现栈

还是先用2个队列模拟栈的出栈和入栈过程，可以得出以下规律：

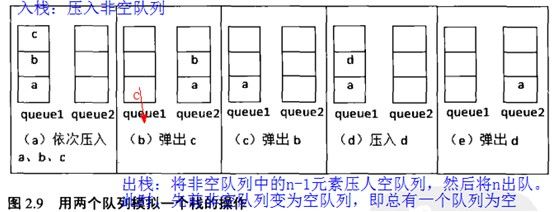
入栈：压入非空的那个队列

出栈：将非空队列中的n-1个元素压入空的队列中，然后将第n个元素出栈。

具体过程见下图（图来自《剑指offer》）

3 如何实现包含获取最小值函数的栈

问题：定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的getMin函数。在该栈中，调用getMin、push及pop的时间复杂度都是O(1).

思路：用一个辅助栈stack2记住每次入栈stack1的当前最小值:在stack1入栈时，往stack2中加入当前最小值；stack1元素出栈时，stack2也出栈一个元素。最小值从stack2中获取及栈顶元素。

4 如何实现包含获取中间值函数的栈

如果能对栈中元素进行排序，那么排序好的中间值即为所求。问题3和问题4的具体代码如下，代码中同时实现了获取栈的最大值、最小值和中间值

public class Stack<E extends Comparable<E>> {
	
	private LinkedList<E> heartStack=new LinkedList<E>(); 
	private LinkedList<E> curMinStack=new LinkedList<E>(); //辅助栈，用于记录当前最小值
	private LinkedList<E> curMaxStack=new LinkedList<E>(); //辅助栈，用于记录当前最大值
	
	public void push(E e){
           heartStack.push(e);
           //当前最小值入栈curMinStack
           E currentMin=curMinStack.peek();
           if(currentMin.compareTo(e)>0){
        	   curMinStack.push(e);
           }//end if
           else
        	   curMinStack.push(currentMin);
           
           //当前最大值入栈curMinStack
           E currentMax=curMinStack.peek();
           if(currentMax.compareTo(e)<0){
        	   curMaxStack.push(e);
           }//end if
           else
        	   curMaxStack.push(currentMax);
	}//end push()
	
	public E pull(){
		if(isEmpty())
			return null;
		else{
			E e=heartStack.poll();
			curMinStack.poll();
			curMaxStack.poll();
			return e;
		}//end else
	}//end pull()
	
	public E getMax(){
		return curMaxStack.peek();
	}//end getMax()
	
	public E getMin(){
		return curMinStack.peek();
	}//end getMin()
	
	public int size(){
		return heartStack.size();
	}//end size()
	
	public boolean isEmpty(){
		return heartStack.isEmpty();
	}//end isEmpty()
	
	public E getMedian(){
		E[] e=(E[]) heartStack.toArray();
		Arrays.sort(e);
		return e[e.length/2];
	}//end getMedian()
	
	public E[] toArray(){
		return (E[])heartStack.toArray();
	}//end toArray()
}

5 如何实现包含获取最小值函数的队列

问题：定义队列的数据结构，请在该类型中实现一个能够得到队列的最小元素的getMin函数。在该队列中，调用getMin、insert及remove的时间复杂度都是O(1).

思路1：用最小堆实现优先队列，获取最小值时间复杂度为O(nlogn)，但优先队列只能获取最小值，remove获取的不是先入队的元素。

思路2：

如果能用栈有效地实现队列，而栈的获取最小值的操作又很容易实现，那么队列的获取最小值的操作也很容易完成。

因为上面可用2个栈实现栈的min函数，而用2个栈可以实现队列。所以可以用已实现了获取最小值的栈stack1和stack2实现队列，而整个队列的最小值从min(stack1.getMin(),stack2.getMin())中获取。具体实现代码见问题6中代码。

6 如何实现具有最大值、最小值和中间值的栈和队列

问题5解决了用O(1)时间获取栈的最小值，那么解决最大值的问题也迎刃而解。对于获取队列的中间值，可以将队列中所有元素排序，然后获取排序后的中间值。

具体实现如下（代码中的stack类为上述问题4中已实现的可以获取最大值和最小值的栈）：

public class ExmaPeekableQueue<E extends Comparable<E>>  implements IExamPeekableQueue{
	Stack stack1=new Stack();
	Stack stack2=new Stack();
	
	@Override
	public void enqueue(Comparable e) {
		stack1.push(e);		
	}//end enqueue()

	@Override
	public Comparable<E> dequeue() {
		if(stack2.isEmpty()){
			stack2.push(stack1.pull());
		}//end if
		
		return stack2.pull();
	}//end dequeue()

	@Override
	public Comparable<E> peekMedian() {
		Comparable[] arr=null; //用于存储队列中当前元素的数组
		
		if(stack1.isEmpty()){
			arr=stack2.toArray();
		}//end if
		else if(stack2.isEmpty()){
			arr=stack1.toArray();
		}//end if
		else{
			arr=new Comparable[size()];
			Comparable[] arrE1=stack1.toArray();
			Comparable[] arrE2=stack2.toArray();
			
			//将2个栈中的元素复制到一个数组中
			int i=0;
            for(;i<stack1.size();i++){
            	arr[i]=arrE1[i];
            }//end for
            
            for(int j=0;j<stack2.size();j++){
            	arr[++i]=arrE2[j];
            }//end for
		}//end else
			
		Arrays.sort(arr);
		return arr[arr.length/2];
	}//end peekMedian()

	@Override
	public Comparable peekMaximum() {
		Comparable max1=stack1.getMax();
		Comparable max2=stack2.getMax();
		
		if(max1.compareTo(max2)>0){
			return max1;
		}//end if
		else
			return max2;
	}

	@Override
	public Comparable<E> peekMinimum() {
		Comparable min1=stack1.getMin();
		Comparable min2=stack2.getMin();
		
		if(min1.compareTo(min2)>0){
			return min2;
		}//end if
		else
			return min1;
	}//end peekMinimum()

	@Override
	public int size() {
		return (stack1.size()+stack2.size());
	}//end size()
}//end class