数据结构和设计模式03（排序）

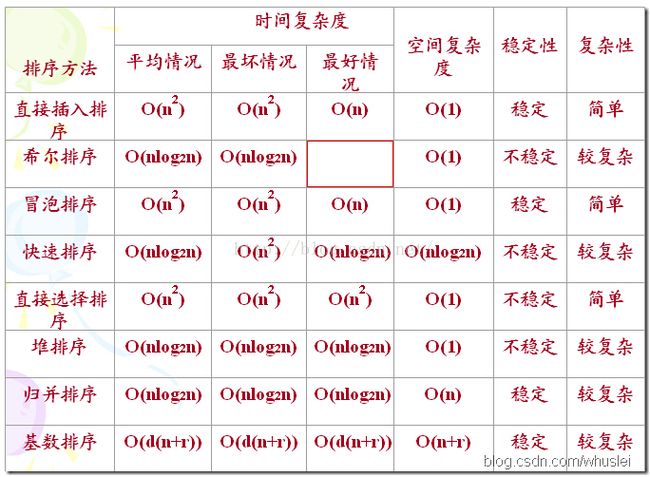
首先看一下各大排序算法的时间空间复杂度：

1.快速排序

伪代码如下

void quick_sort (int a[], int p, int r)  
{  
    if (<span style="color:#ff0000;">p < r</span>)  //终止条件
    {  
        int q = partition (a, p, r);  
        quick_sort (a, p, q - 1);  
        quick_sort (a, q + 1, r);  
    }  
}

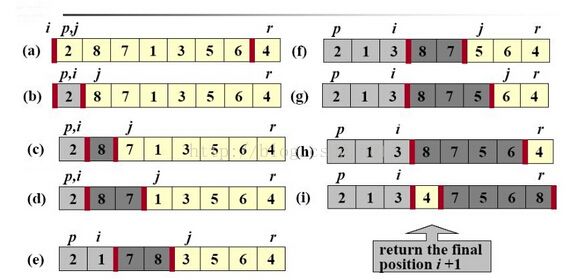
其中，partion（）函数是重点，主要思想如下图。

注意：返回值是位置（下标），因为快排是就地排序，所以函数参数为原来数组，输出还是原来数组（排好序）。

上图的主要在于：1）递归函数终止条件p<r;

2)用i,j来记录每次排序一个元素后，大于key和小于关键字的尾部位置。

理解以上两点编程很容易，此处略。

2.冒泡排序

关键：每次两两比较，不满足不等式，则交换位置（由此可知是双重for循环解决问题），所以每次只能选出一个最大（或者最小）。理解原理后，代码也很简单，略。示意例子如下：

原始待排序数组| 6 | 2 | 4 | 1 | 5 | 9 |

第一趟排序(外循环)

第一次两两比较6 > 2交换(内循环)

交换前状态| 6 | 2 | 4 | 1 | 5 | 9 |

交换后状态| 2 | 6 | 4 | 1 | 5 | 9 |

 

第二次两两比较,6 > 4交换

交换前状态| 2 | 6 | 4 | 1 | 5 | 9 |

交换后状态| 2 | 4 | 6 | 1 | 5 | 9 |

 

第三次两两比较,6 > 1交换

交换前状态| 2 | 4 | 6 | 1 | 5 | 9 |

交换后状态| 2 | 4 | 1 | 6 | 5 | 9 |

 

第四次两两比较,6 > 5交换

交换前状态| 2 | 4 | 1 | 6 | 5 | 9 |

交换后状态| 2 | 4 | 1 | 5 | 6 | 9 |

 

第五次两两比较,6 < 9不交换

交换前状态| 2 | 4 | 1 | 5 | 6 | 9 |

交换后状态| 2 | 4 | 1 | 5 | 6 | 9 |

 

第二趟排序(外循环)

第一次两两比较2 < 4不交换

交换前状态| 2 | 4 | 1 | 5 | 6 | 9 |

交换后状态| 2 | 4 | 1 | 5 | 6 | 9 |

 

第二次两两比较,4 > 1交换

交换前状态| 2 | 4 | 1 | 5 | 6 | 9 | 
交换后状态| 2 | 1 | 4 | 5 | 6 | 9 |

 ... 

第三趟排序(...) 

第四趟排序(外循环)无交换

第五趟排序(外循环)无交换

排序完毕,输出最终结果1 2 4 5 6 9

3.希尔（shell）排序

来源：http://www.cnblogs.com/kkun/archive/2011/11/23/2260288.html

希尔排序Shell Sort是基于插入排序的一种改进,同样分成两部分,

第一部分,希尔排序介绍

第二部分,如何选取关键字,选取关键字是希尔排序的关键

第一块希尔排序介绍

准备待排数组[6 2 4 1 5 9]

首先需要选取关键字,例如关键是3和1(第一步分成三组,第二步分成一组),那么待排数组分成了以下三个虚拟组:

[6 1]一组

[2 5]二组

[4 9]三组

看仔细啊,不是临近的两个数字分组,而是3(分成了三组)的倍数的数字分成了一组,

就是每隔2个数取一个,每隔2个再取一个,这样取出来的数字放到一组,

把它们当成一组,但不实际分组,只是当成一组来看,所以上边的"组"实际上并不存在,只是为了说明分组关系

对以上三组分别进行插入排序变成下边这样

[1 6] [2 5] [4 9]

具体过程:

[6 1]6和1交换变成[1 6]

[2 5]2与5不动还是[2 5]

[4 9]4与9不动还是[4 9]

第一趟排序状态演示:

待排数组:[6 2 4 1 5 9]

排后数组:[1 2 4 6 5 9]

第二趟关键字取的是1,即每隔0个取一个组成新数组,实际上就是只有一组啦,隔一取一就全部取出来了嘛

此时待排数组为:[1 2 4 6 5 9]

直接对它进行插入排序

还记得插入排序怎么排不（就是玩扑克插入牌）?复习一下

[1 2 4]都不用动,过程省略,到5的时候,将5取出,在前边的有序数组里找到适合它的位置插入,就是4后边,6前边

后边的也不用改,所以排序完毕

顺序输出结果:[1 2 4 5 6 9]

第二块希尔排序的关键是如何取关键字,因为其它内容与插入排序一样

增量的取值规则为第一次取总长度的一半,第二次取一半的一半,依次累推直到1为止,刚从下文中看到的这一段描述,感谢!

3.选择排序：

选择排序的思想非常直接，不是要排序么？那好，我就从所有序列中先找到最小的，然后放到第一个位置。之后再看剩余元素中最小的，放到第二个位置……以此类推，就可以完成整个的排序工作了。可以很清楚的发现，选择排序是固定位置，找元素。相比于插入排序的固定元素找位置，是两种思维方式。不过条条大路通罗马，两者的目的是一样的。

4.归并排序

原理：将原序列划分为有序的两个序列，然后利用归并算法进行合并，合并之后即为有序序列。

要点：归并、分治（分治很简单，注意终止条件，合并是重点）

	Void MergeSort(Node L[], int m, int n)
	{
		Int k;
		If(m < n)
		{
			K = (m + n) / 2;
			MergeSort(L, m, k);
			MergeSort(L, k + 1, n);
			Merge(L, m, k, n);//这个函数的实现是重点
		}
	}
		

5.基排序

原理：将数字按位数划分出n个关键字，每次针对一个关键字进行排序，然后针对排序后的序列进行下一个关键字的排序，循环至所有关键字都使用过则排序完成。

要点：对关键字的选取（先排低位，后排高位），元素分配收集。

6.堆排序

堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。

堆排序的重点：就地排序，下标的推算关系(下面的例子都是堆顶下标为1开始)

	parent(i)
		return |_ i/2 _|;
	left(i)
		return 2*i;
	right(i)
		return 2*i + 1;

给定一个数组A[1...n];则

A[( |_ n/2 _| +1)...n]

全是树中的叶子。明白以上两点很重要，下面介绍保持堆的性质：

void MAX_HEAPIFY(int *A, int heap_size, int i)   //i 为待处理保持性质的结点下标
{
        int l = 2 * i + 1;                       //左孩子
        int r = 2 * i + 2;                       //右孩子
        int largest = i;
        if(l < heap_size && A[largest] < A[l])   // 左孩子数值大
        {
            largest = l;
        }
　　　　　if(r < heap_size && A[largest] < A[r])   //右孩子数值大
        {
            largest = r;
        }

        if(largest != i)
        {
            int tmp = A[i];
            A[i] = A[largest];
            A[largest] = tmp;
            MAX_HEAPIFY(A, heap_size, largest); //再从数值大的结点继续往下递归处理
        }
}

基本思路，从下标i开始，比较A[i],left[i]和right[i]，选出最大的值作为父节点，被交换的子节点再一次迭代（如果没有进行交换，算法停止）。

有了保持堆的性质，则对堆的每一个非叶子节点，从下往上调用MAX_HEAPIFY则就建立一个堆。

void BUILD_MAX_HEAP(int *A, int array_size, int heap_size)
{
        int i;
        for (i=array_size/2; i>=0; i--)
        {
            MAX_HEAPIFY(A, heap_size, i);
        }
}

建立了堆后，就可以进行堆排序了：根节点和堆尾节点（叶子）交换位置，然后调用MAX_HEAPIFY,重复这个过程。