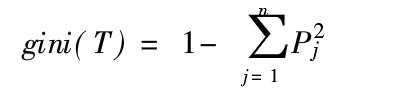数据挖掘笔记-分类-决策树-SLIQ和SPRINT

接着上面说下决策树的一些其他算法：SLIQ、SPRINT、CART。这些算法则是根据Gini指标来计算的。

 

基尼指数（Gini）

Pj为类j出现的频率

如果集合T分成两部分T1和T2，分别对应m1和m2条记录，那么这个分割的基尼指数就是:

选择最小gini作为分割的标准。其中需要注意的是分割点选择：如果是数值或连续性字段，可能的分割点是每两个值的中点；如果是离散字段，可能的分割点是属性值的所有子集。

 

SLIQ(Supervised Learning In Quest)

SLIQ算法对C4.5决策树分类算法的实现方法进行了改进，在决策树的构造过程中采用了“预排序”和“广度优先策略”两种技术。

1) 预排序。对于连续属性在每个内部结点寻找其最优分裂标准时，都需要对训练集按照该属性的取值进行排序，而排序是很浪费时间的操作。为此，SLIQ算法采用了预排序技术。所谓预排序，就是针对每个属性的取值，把所有的记录按照从小到大的顺序进行排序，以消除在决策树的每个结点对数据集进行的排序。具体实现时，需要为训练数据集的每个属性创建一个属性列表，为类别属性创建一个类别列表。

2) 广度优先策略。在C4.5算法中，树的构造是按照深度优先策略完成的，需要对每个属性列表在每个结点处都进行一遍扫描，费时很多，为此，SLIQ采用广度优先策略构造决策树，即在决策树的每一层只需对每个属性列表扫描一次，就可以为当前决策树中每个叶子结点找到最优分裂标准。

SLIQ利用三中数据结构来构造树，分别是属性表、类表和类直方图。

SLIQ算法在建树阶段,对连续属性采取预先排序技术与广度优先相结合的策略生成树,对离散属性采取快速求子集算法确定划分条件。

具体步骤如下:

step1:建立类表和各个属性表,并且进行预先排序,即对每个连续属性的属性表进行独立的排序,以避免在每个节点上都要给连续属性值重新排序;

step2:如果每个叶子节点中的样本都能归为一类,则算法停止;否则转step3;

step3:利用属性表计算gini值，选择最小gini值的属性和分割点作为最佳划分;

step4:根据step3得到的最佳划分节点,判断为真的样本划分为左孩子节点,否则划分为右孩子节点.这样就构成了广度优先的生成树策略;

step5:更新类表中的第二项,使之指向样本划分后所在的叶子节点;

step6:跳转到step2

SLIQ优异性能:

可伸缩性良好:缩短学习时间、处理常驻磁盘的数据集能力、处理结果的准确性.

缺点：

1)由于需要将类别列表存放于内存,而类别列表的元组数与训练集的元组数是相同的,这就一定程度上限制了可以处理的数据集的大小。

2) 由于采用了预排序技术，而排序算法的复杂度本身并不是与记录个数成线性关系，因此，使得SLIQ算法不可能达到随记录数目增长的线性可伸缩性。

 

SPRINT(Scalable Parallelizable Induction of Classification Tree)

SPRINT算法是一种可扩展的、可并行的归纳决策树,它完全不受内存限制,运行速度快,且允许多个处理器协同创建一个决策树模型.

SPRINT算法是对SLIQ算法的改进,其目的有两个:一是为了能够更好的并行建立决策树，二是为了使得决策树适合更大的数据集. 

SPRINT算法定义了两种数据结构,分别是属性表与直方图.属性表由一组三元组<属性值、类别属性、样本号>组成,它随节点的扩张而划分,并归附于相应的子节点.

与SLIQ算法不同,SPRINT算法采取传统的深度优先生成树策略,具体步骤如下:

step1:生成根节点,并为所有属性建立属性表,同时预先排序连续属性的属性表;

step2:如果节点中的样本都能归为一类,则算法停止;否则转step3;

step3:利用属性表寻找拥有最小gini值的划分作为最佳划分方案.算法依次扫描该节点上的每张属性表;

step4:根据划分方案,生成该节点的两个子节点;

step5:划分该节点上的各属性表;

step6:跳转到step2

 

SPRINT算法的优点是在寻找每个结点的最优分裂标准时变得更简单。其缺点是对非分裂属性的属性列表进行分裂变得很困难。解决的办法是对分裂属性进行分裂时用哈希表记录下每个记录属于哪个孩子结点，若内存能够容纳下整个哈希表，其他属性列表的分裂只需参照该哈希表即可。由于哈希表的大小与训练集的大小成正比，当训练集很大时，哈希表可能无法在内存容纳，此时分裂只能分批执行，这使得SPRINT算法的可伸缩性仍然不是很好。

CART(Classification And Regression Tree)

分类回归树算法：CART算法采用一种二分递归分割的技术，将当前的样本集分为两个子样本集，使得生成的的每个非叶子节点都有两个分支。因此，CART算法生成的决策树是结构简洁的二叉树。

分类树两个基本思想：第一个是将训练样本进行递归地划分自变量空间进行建树的想法，第二个想法是用验证数据进行剪枝。

 

这里只对SPRINT算法用Java进行了简单实现:

@Override
public Object build(Data data) {
	//对数据集预先判断，特征属性为空时候选取最多数量的类型,数据集全部为统一类型时候直接返回类型
	Object preHandleResult = preHandle(data);
	if (null != preHandleResult) return preHandleResult;
	//创建属性表
	Map<String, List<Attribute>> attributeTableMap = 
			new HashMap<String, List<Attribute>>();
	for (Instance instance : data.getInstances()) {
		String category = String.valueOf(instance.getCategory());
		Map<String, Object> attrs = instance.getAttributes();
		for (Map.Entry<String, Object> entry : attrs.entrySet()) {
			String attrName = entry.getKey();
			List<Attribute> attributeTable = attributeTableMap.get(attrName);
			if (null == attributeTable) {
				attributeTable = new ArrayList<Attribute>();
				attributeTableMap.put(attrName, attributeTable);
			}
			attributeTable.add(new Attribute(instance.getId(), 
					attrName, String.valueOf(entry.getValue()), category));
		}
	}
	//计算属性表的基尼指数
	Set<String> attributes = data.getAttributeSet();
	String splitAttribute = null;
	String minSplitPoint = null;
	double minSplitPointGini = 1.0;
	for (Map.Entry<String, List<Attribute>> entry : attributeTableMap.entrySet()) {
		String attribute = entry.getKey();
		if (!attributes.contains(attribute)) {
			continue;
		}
		List<Attribute> attributeTable = entry.getValue();
		Object[] result = calculateMinGini(attributeTable);
		double splitPointGini = Double.parseDouble(String.valueOf(result[1]));
		if (minSplitPointGini > splitPointGini) {
			minSplitPointGini = splitPointGini;
			minSplitPoint = String.valueOf(result[0]);
			splitAttribute = attribute;
		}
	}
	System.out.println("splitAttribute: " + splitAttribute);
	TreeNode treeNode = new TreeNode(splitAttribute);
		
	//根据分割属性和分割点分割数据集
	attributes.remove(splitAttribute);
	Set<String> attributeValues = new HashSet<String>();
	List<List<Instance>> splitInstancess = new ArrayList<List<Instance>>();
	List<Instance> splitInstances1 = new ArrayList<Instance>();
	List<Instance> splitInstances2 = new ArrayList<Instance>();
	splitInstancess.add(splitInstances1);
	splitInstancess.add(splitInstances2);
	for (Instance instance : data.getInstances()) {
		Object value = instance.getAttribute(splitAttribute);
		attributeValues.add(String.valueOf(value));
		if (value.equals(minSplitPoint)) {
			splitInstances1.add(instance);
		} else {
			splitInstances2.add(instance);
		}
	}
	attributeValues.remove(minSplitPoint);
	StringBuilder sb = new StringBuilder();
	for (String attributeValue : attributeValues) {
		sb.append(attributeValue).append(",");
	}
	if (sb.length() > 0) sb.deleteCharAt(sb.length() - 1);
	String[] names = new String[]{minSplitPoint, sb.toString()};
	for (int i = 0; i < 2; i++) {
		List<Instance> splitInstances = splitInstancess.get(i);
		if (splitInstances.size() == 0) continue;
		Data subData = new Data(attributes.toArray(new String[0]),
				splitInstances);
		treeNode.setChild(names[i], build(subData));
	}
	return treeNode;
}

/** 计算基尼指数*/
public Object[] calculateMinGini(List<Attribute> attributeTable) {
	double totalNum = 0.0;
	Map<String, Map<String, Integer>> attrValueSplits = 
			new HashMap<String, Map<String, Integer>>();
	Set<String> splitPoints = new HashSet<String>();
	Iterator<Attribute> iterator = attributeTable.iterator();
	while (iterator.hasNext()) {
		Attribute attribute = iterator.next();
		String attributeValue = attribute.getValue();
		splitPoints.add(attributeValue);
		Map<String, Integer> attrValueSplit = attrValueSplits.get(attributeValue);
		if (null == attrValueSplit) {
			attrValueSplit = new HashMap<String, Integer>();
			attrValueSplits.put(attributeValue, attrValueSplit);
		}
		String category = attribute.getCategory();
		Integer categoryNum = attrValueSplit.get(category);
		attrValueSplit.put(category, null == categoryNum ? 1 : categoryNum + 1);
		totalNum++;
	}
	String minSplitPoint = null;
	double minSplitPointGini = 1.0;
	for (String splitPoint : splitPoints) {
		double splitPointGini = 0.0;
		double splitAboveNum = 0.0;
		double splitBelowNum = 0.0;
		Map<String, Integer> attrBelowSplit = new HashMap<String, Integer>();
		for (Map.Entry<String, Map<String, Integer>> entry : attrValueSplits.entrySet()){
			String attrValue = entry.getKey();
			Map<String, Integer> attrValueSplit = entry.getValue();
			if (splitPoint.equals(attrValue)) {
				for (Integer v : attrValueSplit.values()) {
					splitAboveNum += v;
				}
				double aboveGini = 1.0;
				for (Integer v : attrValueSplit.values()) {
					aboveGini -= Math.pow((v / splitAboveNum), 2);
				}
				splitPointGini += (splitAboveNum / totalNum) * aboveGini;
			} else {
				for (Map.Entry<String, Integer> e : attrValueSplit.entrySet()) {
					String k = e.getKey();
					Integer v = e.getValue();
					Integer count = attrBelowSplit.get(k);
					attrBelowSplit.put(k, null == count ? v : v + count);
					splitBelowNum += e.getValue();
				}
			}
		}
		double belowGini = 1.0;
		for (Integer v : attrBelowSplit.values()) {
			belowGini -= Math.pow((v / splitBelowNum), 2);
		}
		splitPointGini += (splitBelowNum / totalNum) * belowGini;
		if (minSplitPointGini > splitPointGini) {
			minSplitPointGini = splitPointGini;
			minSplitPoint = splitPoint;
		}
	}
	return new Object[]{minSplitPoint, minSplitPointGini};
}

代码托管:https://github.com/fighting-one-piece/repository-datamining.git