Cracking the coding interview--Q2.5

Cracking the coding interview--Q2.5

December 17, 2012

作者：Hawstein
出处： http://hawstein.com/posts/2.5.html
声明：本文采用以下协议进行授权：  自由转载-非商用-非衍生-保持署名|Creative Commons BY-NC-ND 3.0 ，转载请注明作者及出处。

题目

原文：

Given a circular linked list, implement an algorithm which returns node at the beginning of the loop.

DEFINITION

Circular linked list: A (corrupt) linked list in which a node’s next pointer points to an earlier node, so as to make a loop in the linked list.

EXAMPLE

Input: A –> B –> C –> D –> E –> C [the same C as earlier]

Output: C

译文：

给定一个循环链表，实现一个算法返回这个环的开始结点。

定义：

循环链表：链表中一个结点的指针指向先前已经出现的结点，导致链表中出现环。

例子：

输入：A –> B –> C –> D –> E –> C [结点C在之前已经出现过]

输出：结点C

解答

关于带环链表的题目，《编程之美》中也有讲过。方法很tricky，设置快慢指针， (快指针速度为2，慢指针速度为1)使它们沿着链表移动，如果这个链表中存在环， 那么快指针最终会追上慢指针而指向同一个结点。接下来的问题是，快指针追上慢指针后， 怎么找到这个环的开始结点？ 现在我们还没有答案，那让我们先来分析一下，快指针会在哪里追上慢指针。

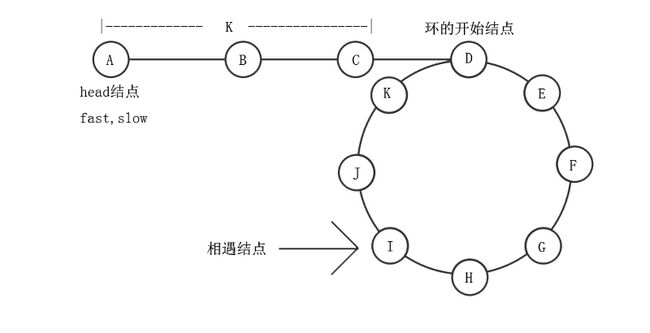
无图无真相，先上图：

设环的开始结点(图中的D)前有k个结点，环有n个结点(上图中n从D到K共8个结点)。 快指针fast和慢指针slow一开始都指向头结点head，它们移动k步可到环的开始结点。 假设慢指针走过m个结点后，快指针追上了它，这时快指针走过了2m个结点。 快指针比慢指针多走过的结点都在环里转圈了，是环中结点数n的整数倍，即：

2m - m = pn --> m = pn, p为正整数

如果头结点是第一个结点的话，那么相遇结点就是第m+1=pn+1个结点(慢指针走了m步)。 当环开始结点为起点1时，相遇结点为第pn+1-k个结点(减去前k个结点)。这pn+1-k 有可能是绕环转了很多圈后的一个数，假设继续走过一些结点，它就绕环刚好q圈， 则从相遇结点需要再经过 qn-(pn+1-k)+1=(q-p)n+k个结点，才能回到环的开始结点(图中结点D)。 由于从相遇结点走回到环的开始结点(图中D)所需要步数一定是小于等于一圈的，因此有

(q-p)n+k <= n 

由于q，p，n，k都是正整数，因此有q-p <= 0，否则上式左边大于右边。 因为q-p <= 0，可以得出上式左边是小于等于k的。即：

(q-p)n+k <= k

如果让快指针在相遇结点继续走，不过这次把速度变成了慢指针一样， 那么它要走(q-p)n+k步到达环开始结点，让慢指针从头结点head开始走， 它要走k步到达环开始结点。最后，它们将在环开始结点处相遇。

这个是怎么得出来的呢？假设快指针走了(q-p)n+k个结点到达环的开始结点，这时， 慢指针也走了(q-p)n+k步，它离环的开始结点还有

k - [ (q-p)n + k ] = (p-q)n (步)

从上面我们知道q-p <= 0，因此p-q >= 0。 这说明慢指针离环开始结点的步数正好是环中结点数的整数倍， 所以当慢指针到达环的开始结点时， 快指针(此时它的速度也是1)刚好在环中转了(p-q)圈，然后和慢指针在环的开始结点处相遇。

代码如下：

node* loopstart(node *head){
    if(head==NULL) return NULL;
    node *fast = head, *slow = head;
    while(fast && fast->next){
        fast = fast->next->next;
        slow = slow->next;
        if(fast==slow) break;
    }
    if(!fast || !fast->next) return NULL;
    slow = head;
    while(fast!=slow){
        fast = fast->next;
        slow = slow->next;
    }
    return fast;
}

这个思路确实很巧很tricky。但，还有没有别的方法呢？更直观更简单的方法。 既然这么问了，当然是有了。:p一个无环的链表，它每个结点的地址都是不一样的。 但如果有环，指针沿着链表移动，那这个指针最终会指向一个已经出现过的地址。 答案是不是已经呼之欲出了。嗯，没错，哈希表！

以地址为哈希表的键值，每出现一个地址，就将该键值对应的实值置为true。 那么当某个键值对应的实值已经为true时，说明这个地址之前已经出现过了， 直接返回它就OK了。

由于C++标准中没有哈希表的操作，我用map进行模拟。不过哈希表的插入和取值操作是O(1) 的时间。而map是由一个RB tree组织，为了维护这个RB tree，插入和取值都会花更多的时 间。

代码如下：

map<node*, bool> hash;
node* loopstart1(node *head){
    while(head){
        if(hash[head]) return head;
        else{
            hash[head] = true;
            head = head->next;
        }
    }
    return head;
}

完整代码如下：

#include <iostream>
#include <map>
using namespace std;

typedef struct node{
    int data;
    node *next;
}node;

node* init(int a[], int n, int m){
    node *head, *p, *q;
    for(int i=0; i<n; ++i){
        node *nd = new node();
        nd->data = a[i];
        if(i==m) q = nd;
        if(i==0){
            head = p = nd;
            continue;
        }
        p->next = nd;
        p = nd;
    }
    p->next = q;
    return head;
}

node* loopstart(node *head){
    if(head==NULL) return NULL;
    node *fast = head, *slow = head;
    while(fast && fast->next){
        fast = fast->next->next;
        slow = slow->next;
        if(fast==slow) break;
    }
    if(!fast || !fast->next) return NULL;
    slow = head;
    while(fast!=slow){
        fast = fast->next;
        slow = slow->next;
    }
    return fast;
}

map<node*, bool> hash;
node* loopstart1(node *head){
    while(head){
        if(hash[head]) return head;
        else{
            hash[head] = true;
            head = head->next;
        }
    }
    return head;
}
int main(){
    int n = 10, m = 9;// m<n
    int a[] = {
        3, 2, 1, 3, 5, 6, 2, 6, 3, 1 
    };
    node *head = init(a, n, m);
    //node *p = loopstart(head);
    node *p = loopstart1(head);
    if(p)
        cout<<p->data<<endl;
    return 0;
}