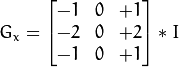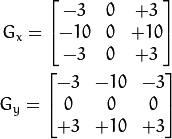Sobel滤波，Laplace滤波介绍与opencv实现

四、高通滤波器        

        前面一章介绍了使用内核矩阵实现低通滤波器，这个滤波器能够删除或者减弱高频分量。这本节中，我们将介绍相反转换的增加高频分量的方法，也就是高通滤波器。主要用于边缘的检测。

4.1 Sobel函数

      opencv中提供了函数cv::Sobel，利用矩阵卷积方法 近似 实现方向导数的计算。
      函数头文件：#include <opencv2/imgproc/imgproc.hpp>

     函数定义：

CV_EXPORTS_W void Sobel( InputArray src, OutputArray dst, int ddepth,
                         int dx, int dy, int ksize=3,
                         double scale=1, double delta=0,
                         int borderType=BORDER_DEFAULT );

     函数使用：

cv::Sobel(image,sobelX,CV_8U,1,0,3,0.4,128);

cv::Sobel(image,sobelY,CV_8U,0,1,3,0.4,128);

     函数参数介绍：

     int ddepth ： 图像深度，或者说图像处理后值的大小范围

    dx，dy        ：决定是对横向和纵向的Sobel处理

     ksize          ：内核矩阵的大小，默认为3

    scale           ：函数处理后值乘以的系数 即 值*scale

   delta             ：函数处理后值的补偿， 即 值*scale + delta

     函数说明：

     函数实现对图像进行求方向导数，当ksize等于3时，方向导数可以近似用内核Gx，Gy和图像I卷积，如下：

        

    水平与垂直相加，也可以近似为： 。

    当然还有另外一个比Sobel函数的近似效果更好的 Scharr函数，其内核矩阵如下:

        

      

4.2 Laplace函数

     在opencv中也提供cv：Laplace函数 ，对图像求二阶导数。因为图像是二维的，所以不用分开求横向和纵向的导数，然后相加。laplace的函数计算如下：，当梯度最大时，二阶导数为0，也能很好的表现出函数边界和轮廓。

    函数定义： 

//! applies Laplacian operator to the image
CV_EXPORTS_W void Laplacian( InputArray src, OutputArray dst, int ddepth,
                             int ksize=1, double scale=1, double delta=0,
                             int borderType=BORDER_DEFAULT );

五、程序实例

#include <iostream>
#include <iomanip>
#include <opencv2/core/core.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include "laplacianZC.h"

int main()
{
	// Read input image
	cv::Mat image= cv::imread("boldt.jpg",0);
	if (!image.data)
		return 0; 

    // Display the image
	cv::namedWindow("Original Image");
	cv::imshow("Original Image",image);
	cv::imwrite("Original Image.jpg",image);

	// Compute Sobel X derivative
	cv::Mat sobelX;
	cv::Sobel(image,sobelX,CV_8U,1,0,3,0.4,128);

    // Display the image
	cv::namedWindow("Sobel X Image");
	cv::imshow("Sobel X Image",sobelX);
	cv::imwrite("Sobel X Image.jpg",sobelX);
	
	// Compute Sobel Y derivative
	cv::Mat sobelY;
	cv::Sobel(image,sobelY,CV_8U,0,1,3,0.4,128);

    // Display the image
	cv::namedWindow("Sobel Y Image");
	cv::imshow("Sobel Y Image",sobelY);
	cv::imwrite("Sobel Y Image.jpg",sobelY);

	// Compute norm of Sobel
	cv::Sobel(image,sobelX,CV_16S,1,0);
	cv::Sobel(image,sobelY,CV_16S,0,1);
	cv::Mat sobel;
	//compute the L1 norm
	sobel= abs(sobelX)+abs(sobelY);

	double sobmin, sobmax;
	cv::minMaxLoc(sobel,&sobmin,&sobmax);
	std::cout << "sobel value range: " << sobmin << "  " << sobmax << std::endl;

	// Print window pixel values
	for (int i=0; i<12; i++) {
		for (int j=0; j<12; j++)
			std::cout << std::setw(5) << static_cast<int>(sobel.at<short>(i+135,j+362)) << " ";
		std::cout << std::endl;
	}
	std::cout << std::endl;
	std::cout << std::endl;
	std::cout << std::endl;

	// Conversion to 8-bit image
	// sobelImage = -alpha*sobel + 255
	cv::Mat sobelImage;
	sobel.convertTo(sobelImage,CV_8U,-255./sobmax,255);

    // Display the image
	cv::namedWindow("Sobel Image");
	cv::imshow("Sobel Image",sobelImage);
	cv::imwrite("Sobel Image.jpg",sobelImage);

	// Apply threshold to Sobel norm (low threshold value)
	cv::Mat sobelThresholded;
	cv::threshold(sobelImage, sobelThresholded, 225, 255, cv::THRESH_BINARY);

    // Display the image
	cv::namedWindow("Binary Sobel Image (low)");
	cv::imshow("Binary Sobel Image (low)",sobelThresholded);
	cv::imwrite("Binary Sobel Image (low).jpg",sobelThresholded);

	// Apply threshold to Sobel norm (high threshold value)
	cv::threshold(sobelImage, sobelThresholded, 190, 255, cv::THRESH_BINARY);

    // Display the image
	cv::namedWindow("Binary Sobel Image (high)");
	cv::imshow("Binary Sobel Image (high)",sobelThresholded);
	cv::imwrite("Binary Sobel Image (high).jpg",sobelThresholded);

	// Compute Laplacian 3x3
	cv::Mat laplace;
	cv::Laplacian(image,laplace,CV_8U,1,1,128);

    // Display the image
	cv::namedWindow("Laplacian Image");
	cv::imshow("Laplacian Image",laplace);
	cv::imwrite("Laplacian Image 3x3 .jpg",laplace);

	// Print window pixel values
	for (int i=0; i<12; i++) {
		for (int j=0; j<12; j++)
			std::cout << std::setw(5) << static_cast<int>(laplace.at<uchar>(i+135,j+362))-128 << " ";
		std::cout << std::endl;
	}
	std::cout << std::endl;
	std::cout << std::endl;
	std::cout << std::endl;

	// Compute Laplacian 7x7
	cv::Laplacian(image,laplace,CV_8U,7,0.01,128);

    // Display the image 
	cv::namedWindow("Laplacian Image");
	cv::imshow("Laplacian Image",laplace);
	cv::imwrite("Laplacian Image 7x7 .jpg",laplace);

	// Print window pixel values
	for (int i=0; i<12; i++) {
		for (int j=0; j<12; j++)
			std::cout << std::setw(5) << static_cast<int>(laplace.at<uchar>(i+135,j+362))-128 << " ";
		std::cout << std::endl;
	}

    // Extract small window
	cv::Mat window(image,cv::Rect(362,135,12,12));
	cv::namedWindow("Image window");
	cv::imshow("Image window",window);
	cv::imwrite("window.bmp",window);

	// Compute Laplacian using LaplacianZC class
	LaplacianZC laplacian;
	laplacian.setAperture(7);
	cv::Mat flap= laplacian.computeLaplacian(image);
	double lapmin, lapmax;
	cv::minMaxLoc(flap,&lapmin,&lapmax);
	std::cout << "Laplacian value range=[" << lapmin << "," << lapmax << "]\n";
	laplace= laplacian.getLaplacianImage();
	cv::namedWindow("Laplacian Image (7x7)");
	cv::imshow("Laplacian Image (7x7)",laplace);
	cv::imwrite("Laplacian Image (7x7).jpg",laplace);
	// Print Laplacian values
	std::cout << std::endl;
	for (int i=0; i<12; i++) {
		for (int j=0; j<12; j++)
			std::cout << std::setw(5) << static_cast<int>(flap.at<float>(i+135,j+362)/100) << " ";
		std::cout << std::endl;
	}
	std::cout << std::endl;

	// Compute and display the zero-crossing points
	cv::Mat zeros;
	zeros= laplacian.getZeroCrossings(lapmax);
	cv::namedWindow("Zero-crossings");
	cv::imshow("Zero-crossings",zeros);
	cv::imwrite("Zero-crossings.jpg",zeros);

	// Compute and display the zero-crossing points (Sobel version)
	zeros= laplacian.getZeroCrossings();
	zeros= laplacian.getZeroCrossingsWithSobel(50);
	cv::namedWindow("Zero-crossings (2)");
	cv::imshow("Zero-crossings (2)",zeros);
	cv::imwrite("Zero-crossings (2).jpg",zeros);

	// Print window pixel values
	for (int i=0; i<12; i++) {
		for (int j=0; j<12; j++)
			std::cout << std::setw(2) << static_cast<int>(zeros.at<uchar>(i+135,j+362)) << " ";
		std::cout << std::endl;
	}

    // Display the image with window
	cv::rectangle(image,cv::Point(362,135),cv::Point(374,147),cv::Scalar(255,255,255));
	cv::namedWindow("Original Image with window");
	cv::imshow("Original Image with window",image);
	cv::imwrite("Original Image with window.jpg",image);

	cv::waitKey();
	return 0;
}

原图形：

程序和图形结果下载：

http://download.csdn.net/detail/skeeee/5763305