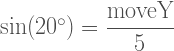使用正弦和余弦来朝着某个角度移动

2. Sine on the Dotted Line: using sine and cosine to move at an angle

This post is about moving at a given angle, or: what use are sine and cosine anyway?

这篇帖子讨论如何根据给定的角度进行运动，即：sin和cos函数如何使用？

Imagine you have a game where you control a spaceship in 2D, flying it around the screen. Positions on the screen in a 2D system use X and Y coordinates, so any movement on the screen is simply an alteration of the X and/or Y coordinates.

想象你在2D游戏中控制一艘飞船在屏幕四周飞行。在2D系统中物体的位置使用x和y坐标来表示，因此物体运动可以简单地看作是其x/y坐标的改变。

Let’s say that the spaceship has a fixed speed of 5 units per frame. If it’s pointing exactly to the right, that’s really easy to implement. You just move 5 units to the right, which means adding 5 to its X coordinate. InGreenfoot, this is:

我们假设飞船的速度固定为每帧5个单位。如果让它完全向右运动，那是很容易实现的。你只需要朝右移动5个单位，即给它的x坐标值增加5。在Greenfoot中的代码如下：

  
  
  
  
setLocation(getX() + 5, getY());

Similarly, if the spaceship is pointing upwards, the code is simple:

类似地，如果飞船向上运动，则代码很简单：

  
  
  
  
setLocation(getX(), getY() - 5);

(Remember that while in maths, positive values on the Y-axis are upwards, in computing they are generally downwards. Seethis note.) But what if the spaceship is pointing at a diagonal angle somewhere between right and upwards, let’s say 20 degrees from horizontal. How many units do you move then?

This problem is a common application of sine and cosine (which fall under the umbrella oftrigonometry). First, let’s draw a little diagram of our problem:

（请记住，在数学中Y轴的正方向是向上的，而在计算机中一般是朝下。）倘若飞船朝着右边和上边之间的某个角度斜线运动的话，比如距离水平方向20度运动，那么需要移动多少单元呢？

这个问题涉及到sin和cos函数（三角学的内容）的基本使用。首先让我们根据问题绘制一幅示意图：

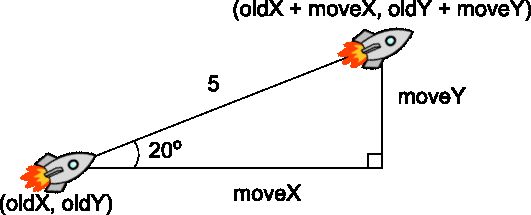
(NB: one thing computing does much better than mathematics is use meaningful variable names, and we will do the same.) So we have a starting position for the spaceship labelled (oldX, oldY) in the bottom left, and a position we want to move to, which will be (oldX + moveX, oldY + moveY). We know the angle (20 degrees in this example) and the distance in a straight line (5, our movement speed). What we need to know are the amounts to move: moveX and moveY.

（注意：计算机信息处理技术比数学好的一点在于能够使用有意义的变量名称，我们将利用这一点。）我们将飞船在左下方的初始位置标记为(oldX, oldY) ，将移动的目标位置标记为(oldX + moveX, oldY + moveY)。我们知道移动的角度（本例中是20度）和直线距离（5，即移动速度）。我们需要知道移动的坐标分量：moveX and moveY。

Calculating the X and Y distances when moving at an angle is where sine and cosine come in useful. Sine and cosine are functions that take an angle, and give back a ratio between two sides of the corresponding right-angle triangle.No matter which two points you are interested in on an X-Y grid system, you can always form a right-angled triangle by drawing connecting lines parallel to the X and Y axes. This is key for much of the use of trigonometry in games and simulations.

sin和cos函数可用于计算斜向运动时的x和y距离分量。sin和cos函数根据给定的角度值返回相关直角三角形的两条直角边的比值。对于直角坐标系中的任意两个点，总是可以通过绘制平行于x轴和y轴的连线来形成一个直角三角形。这是游戏及模拟开发中应用三角学的关键。

Back in maths class, you might have tried to memorise which sides sine and cosine refer to, using an acronym for the letter jumble SOHCAHTOA. Nowadays you can google it, or just go straight to wikipedia (score one for computing!). Here is the relevant sidebox fromthe current wikipedia article:

倘若回到数学课堂上，你或许得试着回忆一下sin和cos函数所涉及的是哪条边。如今你可以用谷歌搜索一下，或者直接去维基百科查看。

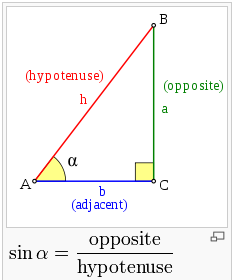
A few notes. The hypotenuse is always the side that is opposite the right-angle: in all our diagrams, this is the slanted diagonal line between the two points we’re interested in. Of the other two sides, the adjacent is the one that is adjacent to the angle you’re interested in (labelled with the greek letter alpha,α, above), and the opposite is the one opposite the angle you’re interested in. So let’s match these two diagrams:

这里有一些说明。斜边始终是与直角相对的：在所有的示意图中，它是连接两个点的倾斜的对角线。邻边是与倾斜角（用希腊字母阿尔法α表示）相邻的边，对边是于倾斜角相对的边。让我们将上面的两幅图匹配一下：

We can see that the hypotenuse is 5, and alpha is 20 degrees. We want to know the length of the adjacent side (the horizontal line, labelled moveX) and the opposite side (the vertical line, labelled moveY). We can adapt the equation from wikipedia to our setting:

图中可以看到斜边值是5，倾斜角的值是20度。我们想知道邻边（水平线，用moveX表示）和对边（垂线，用moveY表示）的长度。可以使用如下公式计算：

The cosine equation is similar, but rather than opposite divided by hypotenuse, it’s adjacent divided by hypotenuse, which in our setting is:

cos函数公式是相似的，只是不再用对边除以斜边，而是用邻边除以斜边，公式如下：

The tiniest bit of re-arrangement in each equation gives:

变形后的公式如下：

   ，    

You can bang that into your calculator right now (being wary ofdegrees vs radians), to get moveX=4.70 (to 2dp) and moveY=1.71 (to 2dp). You can always sanity check those figures using good old pythagoras: it should be the case that (or near enough, given that we’ve rounded).

现在可以直接进行计算了（主意角度与弧度的区别），结果为moveX=4.70 (to 2dp)，moveY=1.71 (to 2dp)。你可以通过勾股定理来检查这些数据：（考虑到四舍五入，结果近似即可）

That’s the calculation for our specific example, but we need to put it in our code. For this, we use Java’s standard maths libraries. Our code for moving at an angle is:

以上是对我们例子的计算，然而需要将它写到代码中去。我们需要用到java中的标准数学库。以下是斜向运动的代码：

  
  
  
  
double radians = Math.toRadians(getRotation());
double moveSpeed = 5;

double moveX = (int)(Math.cos(radians) * moveSpeed);
double moveY = (int)(Math.sin(radians) * moveSpeed);

setLocation(getX() + (int)moveX, getY() + (int)moveY);

For our rocket ship, that’s all you need to move at an angle. This function is so useful that in Greenfoot it’s now provided for you: you can callmove(5);, which will perform the above calculations for you, and move 5 units at the current rotation. But don’t feel cheated: understanding this use of sine and cosine is necessary for us to build more interesting games in future posts.

对于我们的飞船，以上代码足以实现斜向运动。Greenfoot将以上代码写成了一个非常实用的函数：你可以调用move(5)，它便会为你执行以上的计算，即根据当前角度值的方向移动5个单位的距离。然而不要感觉受到欺骗：理解sin和cos的用法对于以后创建更加有趣的游戏是非常必要的。

I’ve made a quick scenario to demonstrate it in action, combining the above code with the usual Greenfoot code for turning based on keyboard control. You canhave a play (use the left and right arrow keys to turn), and download the project to look at the code in Greenfoot .