正定对称矩阵快速求解
作者:JHJ([email protected])
日期:2012/08/24
欢迎转载,请注明出处
关于正定稀疏矩阵的一种快速求解方法。对Cholesky分解的一种优化。四年前的论文,当时做语音信号处理时写的,现在分享给大家。具体内容见点这里。
1.大型稀疏正定矩阵的cholesky分解
文[1]利用无向图来确定cholesky分解的下三角矩阵的非零结构图,提出了两种算法,即消去图和通过商图找顶点的可达集。本文主要利用有向图来确定cholesky分解的下三角矩阵的非零结构图,采用有向图算法可以进一步减小算法的时间和空间复杂度,提出利用动态规划思想确定顶点的终点集(即文[1]可达集的概念)以及有向图中的消去图算法。本文同时给出了这两种算法的数据结构,这种数据结构有利于大型稀疏矩阵的压缩。
1.1标准choleskey算法时间复杂度分析
本文介绍直接法求解对称正定线性方程组
Ax = b, (1.1)
其中A是N阶大型稀疏对称正定矩阵。应用cholesky分解求解(1.1)是一稳定有效的方法。Cholesky分解的MATLAB算法如下[1]:
for j = 1 : n 1
for i = j : n 2
v(i) = aij 3
for k = 1 : j – 1 4
v(i) = v(i) - gjk *gik; 5
end 6
gij = v(i) /![]() ; 7
; 7
end 8
end 9
其中gij为对称正定矩阵A经过Cholesky分解得到的下三角矩阵L。
记s(i)为程序中第i行程序运行的次数。
1.2理论上稀疏矩阵choleskey分解最小时间复杂度
标准choleskey分解计算了下三角矩阵L的主对角线及以下元素的所有值。但是若L为稀疏矩阵,如果我们能事先知道L中非零元素的位置,则我们只需要这些非零元值。显然,这可以很好的降低时间复杂度。
若我们只计算L中非零元的值,则我们可知,
对于第2个for循环,第j列有δ×(n-j+1)个非零元素。
对于第3个for循环,由于第i行有i×δ个非零元素,如果我们只操作第j行的非零元素,则此循环平均次数为t/n。此时
比较式(1.2)、(1.3)、(1.4)我们发现,当我们只优化前两个for循环时,时间复杂度可减少δ倍,当我们优化第三个for循环时,时间复杂度可减少δ2倍。这就是理论上choleskey分解最优值。若L为稀疏矩阵,一般δ=0.05[2],若能实现式(1.4)的优化,则时间性能可以提高约1/400倍。
优化后的choleskey分解算法的伪代码如下:
for j = 1 : n 1
对第j列每个非零元素i 2
v(i) = aij 3
对每个gjk不为零的k(k = 1:j-1) 4
v(i) = v(i) - gjk *gik; 5
end 6
gij = v(i) / ![]() ; 7
; 7
end 8
end 9
1.3稀疏矩阵choleskey优化――矩阵操作
(1) choleskey分解算法分析
设A是一个N阶对称稀疏矩阵,A的非零结构记为Nonz(A)= {(i, j)| aij≠ 0, i≠ j}。设经Cholesky分解,A被分解为A = LLT,其中L为下三角矩阵。称F=L+LT为A的填充矩阵,F的非零结构为Nonz(F)={(i, j )| gij≠ 0, i ≠ j}。
Cholesky分解中,有关系式
其中i为矩阵A的行,j为矩阵A的列。我们所关心的是gij什么情况等于零,显然有以下三种情况:
这三种情况都可能发生,只有第(3)种情况下,我们是无需计算就可以确定gij的值,其它两种情况我们都需要计算才可以确定gij的值。
因此我们可以得到结论:
gij是需要计算的,如果 (i , j)满足以下两个条件的任何一个:(1) aij ≠0;(2) aij = 0,且gjk≠ 0,gik≠ 0 (k < j < i, )。
我们称gij是一个填充元素,如果(i, j)满足条件(2)。
(2) 优化算法实现
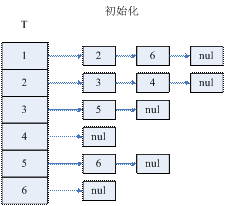
初始条件:L为N×N其中所有元素初始化为零的空矩阵。其中aij为A中第i行第j列的元素,gij为L中第i行第j列矩阵,gij = 0表示(i, j)元在choleskey分解中无需被计算。
//(i , j)满足aij≠0
for i= 1 to n
for j = 1 to i
if (aij≠ 0 ) gij = 1
end for
end for
//(i , j)满足aij = 0,且gjk≠ 0且gik≠ 0
count = 0; //count记录第j列中主对角线下面非零元的个数
for j = 1 to n
for i = j+1 to n
if (aij≠ 0)
count = count +1;
tmp[count] = i; //记录第j列中主对角线下面非零元的行号
end for
for k = 1 to count-1
for i = k+1 to count
g[tmp[i]][tmp[k]] = 1
end for
end for
end for
(3) 优化复杂度分析
则此程序的时间复杂度为
考虑平均情况,count = t/n,代入式(4.2)得时间复杂度为![]() 。
。
1.4稀疏矩阵choleskey优化――图论应用
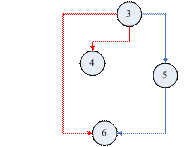
用 G(X, E)表示一个有向图,其中,X是图G顶点的集合,E是X中有序顶点对所构成的边的集合。图G(X, E)的一个排序α是{1, 2, ……, N}到X的一个映射,N是G中顶点的个数,以G(Xα, Eα)记之。
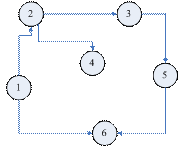
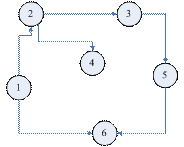
现在建立图与矩阵之间的关系。设A = (aij)是一个N阶对称正定矩阵(根据A的对称性,矩阵中只需要存储其下三角部分即可,这并不影响cholesky分解,同时可以节省内存空间),它所对应的图为GA = (XA, EA)。其顶点xi = aii(i = 1 to N),其边<xj, xi> = aij(aij≠ 0 且j <= i)。图3.2.1、3.2.2、3.2.3分别给出了一个有向图及其两种表现形式。其中①表示矩阵的第i个对角线元素,它对应图的第i个顶点,”x”表示对角线以外的非零元素,它对应图中的边。
图 1.4.1 一个有向图
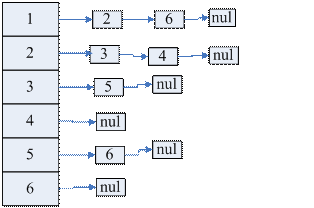
图 1.4.2 图的邻接矩阵表示 图 1.4.3 图的邻接表表示
我们可以将矩阵A的下三角部分表示成图的形式。下面分析如何从A的非零元结构图得到cholesky分解下三角矩阵L的非零结构图。
定义3.2.1图G = (X, E)中,若<x, y>属于E,则<x,y>表示从x到y的一条弧,且称x为起始点(Initial node),y为终端点(Terminal node)。
图1.4.4 弧的示意图
本文中,<x,y>属于E的必要条件是x < y。即起始点的序号要大于终端点的序号。
在1.3中,我们有这样一个结论:gij是需要计算的,如果 (i , j)满足以下两个条件的任何一个:(1) aij ≠0;(2) aij = 0,且gjk≠ 0且gik≠ 0 (k < j < i, )。
此结论在有向图中是这样的:
结论(1):i到j的一条弧存在,如果<i, j>满足以下两个条件中的任何一个:(1) <i, j>∈E;(2)<i, j>不属于E,但存在顶点k (k < i <j, ),使<k, i>∈E且<k, j>∈E。
矩阵中aij ≠0在有向图中的意义为<i, j>存在。
结论(1)确定了弧<i,j>存在的条件。对结论(1)的第(2)种情况,图G发生了“增弧现象”,这对应矩阵中的“填充现象”。
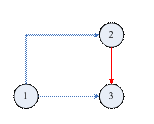
图1.4.5 增弧现象示意图
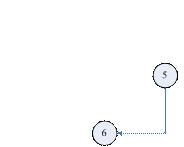
如图1.4.5所示,G(X, E)中,X = {1, 2, 3},E = {<1,2>, <1,3>},但是对于<2, 3>,图中存在顶点1(1 < 2 < 3),使<1,2>和<1,3>属于E,因此根据结论(1),发生了“增弧现象”,即G中增加了一条弧<2,3>。
现在的问题是:对任意顶点j (j = 1 to n),需要找到其所有的增弧。如果把顶点j看成起始点的话,则需要找到j的所有增加的终端点。
算法(1)
记点集T(j) = {i | <j,i>∈E, j < i},称T(j)为以顶点j为的起始点的弧的终端点集。记I(j) = {i | <i,j>∈E, i < j },称I (j)为以顶点j为的终端点的弧的起始点集。
若要确定T(j),则必须先要确定T(k),k∈I(j)。
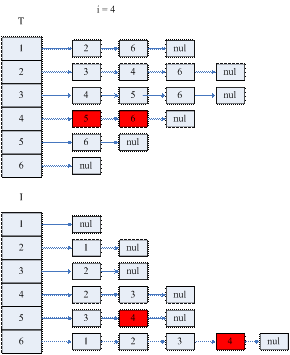
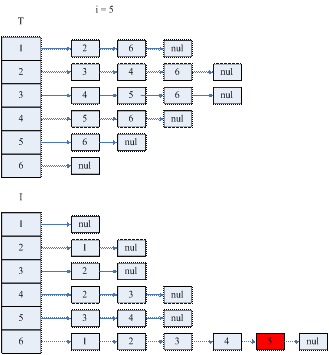
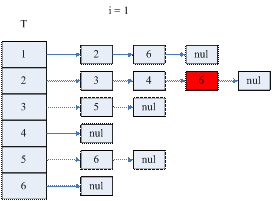
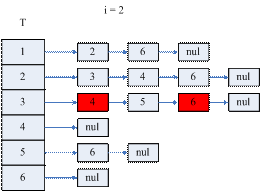
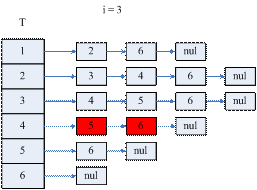
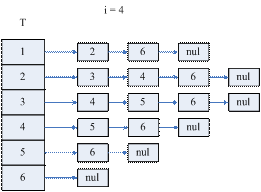
因为这里有子问题重叠现象,且需要自底向上的求解问题,因此可以采用动态规划思想来解决这个问题,即我们依次求解I (1)、T(1)、I (2)、T(2)、……、I (n)、T(n),这样便可以确定L的非零元结构了。即在矩阵L中,(i, j)元是需要求解的,若(i, j) ∈{(i,j) | i∈T(j)或i = j }。
算法(1)描述如下:
根据矩阵A先初始化T(i)
for i = 1 to n
I(i) = φ
I(k) ← 1, ( k∈T(1) )
end for
for i = 2 to n-1
T(i) ← t, ( t∈T(k), k∈I(i), i < t )
I(k) ← i, ( k∈T(i) )
end for
如果采用图1.4.3的链表结构,则需要两个此结构T和I,T用来存放T(i),I用来存放I(i)。
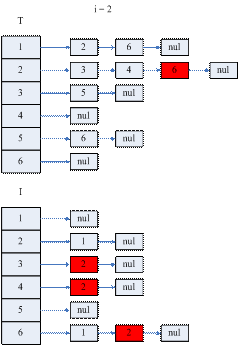
图1.4.6 算法(1)的示意图
i = 5时T的结构就确定了L的结构。
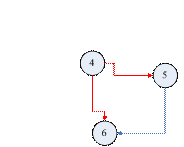
算法(2)
在文[1]消去图算法种,若要消去第i个顶点,记第i个顶点的相邻点有n个,则需要n2次操作,而采用有向图的消去图算法,则只需n-1次操作,显然这种算法可以很好的减小时间复杂度。其算法如下:
算法描述
for i = 1 to n-2
a = min(T(i));
b∈{x | x > a, x∈T(i)};
T(a) ← b;
end for
图1.4.5(图1.4.1)的最终图
图1.4.6 (图1.4.4) 的表示图
参考文献
[1] 图论在稀疏对称矩阵中的应用
[2] 数据结构