hdu1255-----覆盖的面积

覆盖的面积

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 3870    Accepted Submission(s): 1906

Problem Description

给定平面上若干矩形,求出被这些矩形覆盖过至少两次的区域的面积.

 

Input

输入数据的第一行是一个正整数T(1<=T<=100),代表测试数据的数量.每个测试数据的第一行是一个正整数N(1<=N&lt;=1000),代表矩形的数量,然后是N行数据,每一行包含四个浮点数,代表平面上的一个矩形的左上角坐标和右下角坐标,矩形的上下边和X轴平行,左右边和Y轴平行.坐标的范围从0到100000.

注意:本题的输入数据较多,推荐使用scanf读入数据.

 

Output

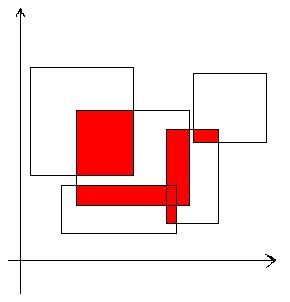
对于每组测试数据,请计算出被这些矩形覆盖过至少两次的区域的面积.结果保留两位小数.

 

Sample Input

   
   
   
   

    
    
    
    2
5
1 1 4 2
1 3 3 7
2 1.5 5 4.5
3.5 1.25 7.5 4
6 3 10 7
3
0 0 1 1
1 0 2 1
2 0 3 1
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    7.63
0.00
   
   
   
   

 

Author

Ignatius.L & weigang Lee

 

Recommend

Ignatius.L   |   We have carefully selected several similar problems for you:   1698  1823  2871  1541  3333 

 

这题用线段树维护时,要多维护一个len2,表示被覆盖至少2次的线段长度, 其他和矩形并一样, 在纸上画一下图就知道为什么了

当add >= 2

区间里被覆盖一次及一次以上的线段长度和被覆盖至少2次的线段长度一样,都是区间长度

当add==1

区间里被覆盖一次及一次以上的线段长度是区间长度, 被覆盖至少2次的线段长度是左右子树被覆盖至少一次的线段长度之和(这些线段在子树上被覆盖一次, 在根上又被覆盖一,所以一共被覆盖2次)

当add == 0

根状态由子树决定

注意特判叶子节点

/*************************************************************************
    > File Name: hdu1255.cpp
    > Author: ALex
    > Mail: [email protected] 
    > Created Time: 2015年01月15日 星期四 17时46分07秒
 ************************************************************************/

#include <map>
#include <set>
#include <queue>
#include <stack>
#include <vector>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 2010;

struct node
{
	double l, r;
	double h;
	int flag;
}lines[N << 1];

struct segment
{
	int l, r;
	int add;
	double len1, len2;
}tree[N << 2];

double xis[N << 1];
int n, cnt;

int cmp (node a, node b)
{
	return a.h < b.h;
}

int BinSearch(double val)
{
	int l = 1;
	int r = cnt;
	int mid;
	while (l <= r)
	{
		mid = (l + r) >> 1;
		if (xis[mid] < val)
		{
			l = mid + 1;
		}
		else if (xis[mid] > val)
		{
			r = mid - 1;
		}
		else
		{
			break;
		}
	}
	return mid;
}

void build (int p, int l, int r)
{
	tree[p].l = l;
	tree[p].r = r;
	tree[p].add = 0;
	tree[p].len1 = 0;
	tree[p].len2 = 0;
	if (l == r)
	{
		return;
	}
	int mid = (l + r) >> 1;
	build (p << 1, l, mid);
	build (p << 1 | 1, mid + 1, r);
}

void pushup (int p)
{
	if (tree[p].add >= 2)
	{
		 tree[p].len2 = xis[tree[p].r + 1] - xis[tree[p].l];
		 tree[p].len1 = tree[p].len2;
	}
	else if (tree[p].add == 1)
	{
		tree[p].len1 = xis[tree[p].r + 1] - xis[tree[p].l];
		if (tree[p].l == tree[p].r)
		{
			tree[p].len2 = 0;
		}
		else
		{
			tree[p].len2 = tree[p << 1].len1 + tree[p << 1 | 1].len1;
		}
	}
	else
	{
		if (tree[p].l == tree[p].r)
		{
			tree[p].len1 = tree[p].len2 = 0;
		}
		else
		{
			tree[p].len1 = tree[p << 1].len1 + tree[p << 1 | 1].len1;
			tree[p].len2 = tree[p << 1].len2 + tree[p << 1 | 1].len2;
		}
	}
}

void update (int p, int l, int r, int val)
{
	if (tree[p].l == l && r == tree[p].r)
	{
		tree[p].add += val;
		pushup (p);
		return;
	}
	int mid = (tree[p].l + tree[p].r) >> 1;
	if (r <= mid)
	{
		update (p << 1, l, r, val);
	}
	else if (l > mid)
	{
		update (p << 1 | 1, l, r, val);
	}
	else
	{
		update (p << 1, l, mid, val);
		update (p << 1 | 1, mid + 1, r, val);
	} 
	pushup (p);
}

int main()
{
	int t;
	double x1, y1, x2, y2;
	scanf("%d", &t);
	while (t--)
	{
		cnt = 0;
		scanf("%d", &n);
		for (int i = 1; i <= n; ++i)
		{
			scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
			lines[i].l = x1;
			lines[i].r = x2;
			lines[i].h = y1;
			lines[i].flag = 1;
			lines[i + n].l = x1;
			lines[i + n].r = x2;
			lines[i + n].h = y2;
			lines[i + n].flag = -1;
			xis[++cnt] = x1;
			xis[++cnt] = x2;
		}
		sort (xis + 1, xis + cnt + 1);
		cnt = unique (xis + 1, xis + cnt + 1) - xis - 1;
		build (1, 1, cnt);
		sort (lines + 1, lines + 2 * n + 1, cmp);
		double ans = 0;
		int l = BinSearch (lines[1].l);
		int r = BinSearch (lines[1].r) - 1;
		update (1, l, r, lines[1].flag);
		for (int i = 2; i <= 2 * n; ++i)
		{
			ans += tree[1].len2 * (lines[i].h - lines[i - 1].h);
			l = BinSearch (lines[i].l);
			r = BinSearch (lines[i].r) - 1;
			update (1, l, r, lines[i].flag);
		}
		printf("%.2lf\n", ans);
	}
	return 0;
}