Hough变换的线段检测

 

   学习Hough变换过程中发现检测线段的算法资料不少，但实际能高效实现的不多。自己也在学习过程，水平问题只能提供思路和部分代码。

 

Hough变换的基本思想：

 

Hough变换的基本思想就是点- 线的对偶性。它是对图像进行某种形式的坐标变换,将原始图像中给定形状的曲线或直线变换成空间中的一个点,在变换空间中形成峰值点。从而使检测整体特性变成检测局部特性,使问题简化。设在原始图像空间( x, y)直线方程为:

y = kx + b;
我们将其转换为极坐标作为变换空间,即:
ρ= xcosθ+ y sinθ

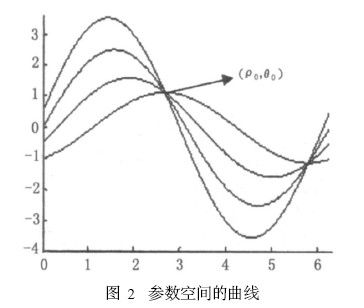
其中,ρ是原点到直线的距离;θ是该直线法线与x轴的夹角。这样空间中的一个点( xi , yi )对应着极坐标中的ρ= xi cosθ+ yi sinθ是一条正弦曲线, 那么原始图像空间中的一条直线上的所有点对应着变换空间的一个曲线族,如图1和图2所示,并且过点(ρ0 ,θ0 ) ,即为参数空间的共线, 也就是图像空间的拟和参数。所以,只要找到这个公共点就可以检测出直线。

 

Hough变换的基本步骤：
(1)首先对图像进行前期预处理, 得到边缘点(二值化的图像)也就是特征点。
(2)设定一个累加器数组, Accumulator (ρ, θ) ,初值为0,对每一个像素点( xi , yi )遍历θ的取值,计算对应的ρ值,如果其值对应累加器数组中某个值,则该累加器值加1。
3)当遍历完所有的( x, y)点以后, 再遍历所有的累加器的值,找出累加器的峰值点,其对应的就是原是图像空间的共线点。

 

直线检测代码：

 //第0步：创建sin,cos表
 /*************************************************************************
   Function Name: _rtCreateSinCos

   Function Action: //第0步：创建sin,cos表

   Input Parameter: NULL

   Output Parameter: sinv--正弦值表
                     cosv--余弦值表

   Return Value: NULL

   Author :  WangFei  2010/4/29   16:12

   Remark:

 *************************************************************************/
 static void _rtCreateSinCos(float* sinv, float* cosv)
 {
     static bool isCreate = false;
     static float sin_tab[361], cos_tab[361];//sin,cos表

     float ratio = 0; //temp
     int inc = 0;

     if (!isCreate)//第一次创建
     {
         for (inc = DEGREES; inc >= 0; inc--)
         {
             ratio = inc * POL2CART;//角度转弧度
             sin_tab[inc] = (float)sin(ratio);
             cos_tab[inc] = (float)cos(ratio);
         }
         isCreate = true;
     }

     memcpy(sinv, sin_tab, sizeof(float)*361);
     memcpy(cosv, cos_tab, sizeof(float)*361);
 }

 /*************************************************************************
   Function Name: _rtImage2Hough

   Function Action: 对图像进行扫描．对于边缘点(x，y)作Hough变换，得到直线r = x*cos(a) + y*sin(a),
                    在Hough平面A[a、r]中、凡是直线经过的象元(a,r)处．使A[a、r] = A[a、r] + 1.

   Input Parameter: src--笛卡尔坐标中的图像数据
                    sinv--正弦值表
                    cosv--余弦值表

   Output Parameter: list--每个图像极坐标数据位置对应的值（笛卡尔坐标中的图像数据直线对应像数的位置数据）

   Return Value: NULL

   Author :  WangFei  2010/4/29   16:14

   Remark:

 *************************************************************************/
 static void _rtImage2Hough(const RtImage* src, CRtList<RtPoint>* list)
 {
     float sin_tab[361], cos_tab[361];//sin,cos表

     //第0步：创建sin,cos表
     _rtCreateSinCos(sin_tab, cos_tab);

     //中间变量
     int   x = 0, y = 0, deg = 0, rad = 0, inc = 0, index = 0;

     int  cartSize = src->height * src->width;//Cartesian坐标大小

     while (inc < cartSize)
     {
         if (255 == (*(src->pData + inc)))
         {
             x = inc % src->width;
             y = inc / src->width;

             for (deg = 0; deg <= DEGREES; deg++)
             {
                 if ( (rad = (int)(x * cos_tab[deg] + y * sin_tab[deg])) > 0)//r = x*cos(a) + y*sin(a)
                 {
                     index = rad * (DEGREES + 1) + deg;
                     (list + index)->Insert_back( rtPoint(x, y) );//添加队列数据//增加Hough平面A[a、r]统计值
                 }
             }
         }
         inc++;
     }
 }

 

线段检测思路：

1，在直线检测到基础上，在极坐标系内对靠近直线统计，使靠近直线为同一直线（滤波作用）。

2，对直线分析其连续性，统计出各线段具体数据（细化）