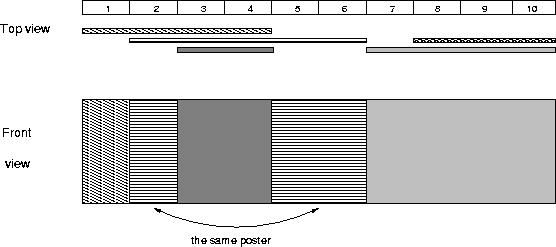
Mayor's posters（线段树区间更新+离散化）
Link：http://poj.org/problem?id=2528
|
Mayor's posters
Description
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections. Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall. Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l
i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l
i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l
i, l
i+1 ,... , ri.
Output
For each input data set print the number of visible posters after all the posters are placed.
The picture below illustrates the case of the sample input. 
Sample Input 1 5 1 4 2 6 8 10 3 4 7 10 Sample Output 4 Source
Alberta Collegiate Programming Contest 2003.10.18
|
用到的线段树功能有:update:成段替换 query:简单hash
AC code：
/*
不离散化势必MLE,此题离散化即是区间压缩，就是把
一些无用的区间进行压缩，而不改变区间的覆盖关系，
从而达到节省空间的目的。
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<queue>
#define LL long long
#define MAXN 40005
using namespace std;
int linecover[MAXN];
LL ans;
struct node{
int l,r,c;
}tree[MAXN*3];
struct linenode{
int id;
int s;
int f;
}p[MAXN*3];
struct lisan{
int id;
int st;
int ed;
}pp[MAXN*3];
bool cmp(linenode x,linenode y)
{
return x.s<y.s;
}
void build(int rt,int s,int e)
{
tree[rt].l=s;
tree[rt].r=e;
tree[rt].c=0;
if(s==e)
{
return;
}
int mid=(s+e)/2;
build(rt*2,s,mid);
build(rt*2+1,mid+1,e);
}
void update(int rt,int l,int r,int cnt)
{
if(tree[rt].l==l&&tree[rt].r==r)
{
tree[rt].c=cnt;
return;
}
int mid=(tree[rt].l+tree[rt].r)/2;
if(tree[rt].c!=0)//pushdown操作
{
tree[rt*2].c=tree[rt*2+1].c=tree[rt].c;
tree[rt].c=0;
}
if(r<=mid)
{
update(rt*2,l,r,cnt);
}
else if(l>mid)
{
update(rt*2+1,l,r,cnt);
}
else
{
update(rt*2,l,mid,cnt);
update(rt*2+1,mid+1,r,cnt);
}
}
void query(int rt,int l,int r)
{
if(tree[rt].c!=0)
{
if(!linecover[tree[rt].c])
{
ans++;
linecover[tree[rt].c]=1;
}
return;
}
int mid=(l+r)/2;
query(rt*2,l,mid);
query(rt*2+1,mid+1,r);
}
int main()
{
int t,n,i,st,ed;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%d%d",&st,&ed);
p[i*2-1].s=st;
p[i*2-1].f=0;
p[i*2-1].id=i;
p[i*2].s=ed;
p[i*2].id=i;
p[i*2].f=1;
}
sort(p+1,p+2*n+1,cmp);
int tmp=p[1].s;
int cnt=1;
/*不知为何，我把下面两行注释掉的代码写在外面poj就会RE,全部写在循环里面才AC*/
//pp[p[1].id].id=p[1].id;
//pp[p[1].id].st=cnt;//排序后第一个点肯定是某一条线段的起点
for(i=1;i<=2*n;i++)//离散化
{
if(tmp!=p[i].s)
{
cnt++;
tmp=p[i].s;
}
pp[p[i].id].id=p[i].id;
if(p[i].f==0)
{
pp[p[i].id].st=cnt;
}
else if(p[i].f==1)
{
pp[p[i].id].ed=cnt;
}
}
memset(linecover,0,sizeof(linecover));
build(1,1,cnt);
for(i=1;i<=n;i++)
{
update(1,pp[i].st,pp[i].ed,pp[i].id);
}
ans=0;
query(1,1,cnt);
cout<<ans<<endl;
}
return 0;
}