岭回归与lasso

作者：金良（[email protected]） csdn博客： http://blog.csdn.net/u012176591

岭回归(ridge regression)

回忆 LR 的优化目标

L=(Y−Xw)T(Y−Xw)

为防止过拟合，增加正则化项 λ||w||2 ，目标函数就变成

L=(Y−Xw)T(Y−Xw)+λ||w||2

对其进行求导，得到

∂L∂w=−2XT(Y−Xw)+2λw

令导数为0，得

w=(XTX+λI)−1XTY

这就是岭回归的公式。

岭回归具有以下优点：

• 在特征数 M 大于样本数 N 时， XTX 不可逆，故不能直接用 LR ，而岭回归就可以。
• 通过引入 λ 惩罚项，防止过拟合。

Lasso

与岭回归不同，lasso增加的正则化项是 λ||w||1 ，目标函数就变成

L=(Y−Xw)T(Y−Xw)+λ||w||1

这个细微的变化，极大增加了计算复杂度，因为其不可直接求导。

前向逐步回归(Forward Stagewise Linear Regression)

前向逐步回归的伪代码：

相关代码：

datas = []
values = []
with open('abalone','r') as f: 
    for line in f: 
        linedata =  line.split('\t')
        datas.append(linedata[0:-1]) #前4列是4个属性的值
        values.append(linedata[-1].replace('\n',''))  #最后一列是类别 
datas = np.array(datas)
datas = datas.astype(float) 
values = np.array(values)
values = values.astype(float) 

N,M =  datas.shape #N是样本数，M是参数向量的维
means = datas.mean(axis=0) #各个属性的均值
stds = datas.std(axis=0) #各个属性的标准差
datas = (datas-means)/stds #标准差归一化
values = (values-values.mean())/values.std() #标准差归一化


fig,axes = plt.subplots(nrows=2,ncols=2,figsize=(8,8))
plt.suptitle(u'Forward Stepwise Regression Example',fontsize = 18) #用中文会出错，不知为何
plt.subplots_adjust(wspace = 0.25,hspace=0.25)
lambds = [0.05,0.5,1.0,3.0]

axes = axes.flatten()
for i in range(4):
    numIt = 600 #迭代次数
    delta = 0.01 # 调整系数
    wlog = np.zeros((numIt,M)) #记录weights的变化
    weights = np.zeros(M) #系数向量
    lambd = lambds[i]

    for it in range(1,numIt):
        Lmin = {'value':np.inf,'loc':np.nan,'sign':np.nan} #记录本次迭代的目标函数最小值
        for m in range(M-1,0,-1):
            for sign in (-1,1):
                wbak = cp.deepcopy(weights)
                wbak[m] += delta*sign
                Lcur = np.linalg.norm(values-np.dot(datas,wbak),2)+ lambd*np.linalg.norm(wbak,1)
                #print m,sign,Lcur
                if Lmin['value'] > Lcur: # 如果目标函数值比当前最优值小
                    Lmin['value'] = Lcur
                    Lmin['loc'] = m
                    Lmin['sign'] = sign
        weights[Lmin['loc']] += delta*Lmin['sign']
        wlog[it,:] = weights[:]
    ax = axes[i]
    for m in range(M):
        ax.plot(wlog[:,m])  
    ax.set_title('lambda='+np.str(lambd),{'fontname':'STFangsong','fontsize':10})
    ax.set_xlabel(u'迭代次数',{'fontname':'STFangsong','fontsize':10})
    ax.set_ylabel(u'各权值系数',{'fontname':'STFangsong','fontsize':10})
savefig('lasso1.png',dpi=300,bbox_inches='tight')

Lasso Shooting Algorithm

如下求导

∂L(w)∂wk=−2∑i=1Nxik(yi−wTxi)=−2∑i=1Nxik(yi−wkTxik−(wTxi−wkTxik))=wk⋅2∑i=1Nx2ik−2∑i=1Nxik(yi−wTxi+wkxik)

令其中

αk=2∑i=1Nx2ik,ck=2∑i=1Nxik(yi−wTxi+wkxik)

,

则可写成

∂L(w)∂wk=αk⋅wk−ck

令 L(w,λ)=L(w)+λ||w||1

则

∂L(w,λ)∂wk=⎧⎩⎨αk⋅wk−ck−λ[−ck−λ,−ck+λ]αk⋅wk−ck+λwk<0wk=0wk>0

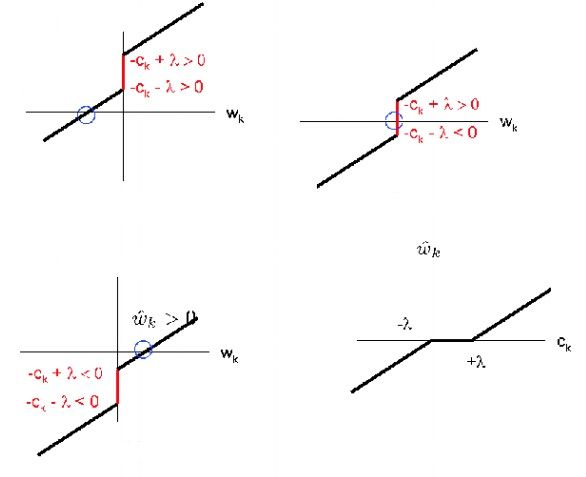
进而可得 wk 的更新公式

wk=⎧⎩⎨(ck+λ)/αk0(ck−λ)/αkck<−λck∈[−λ,λ]ck>−λ

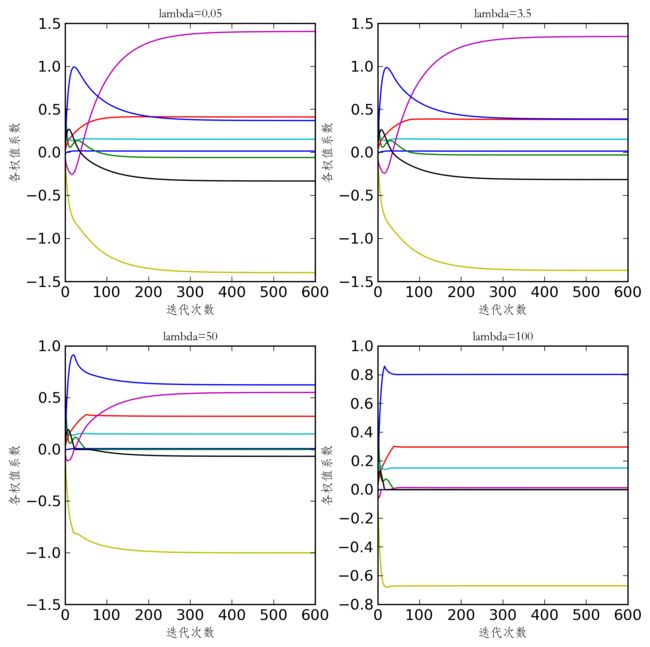
fig,axes = plt.subplots(nrows=2,ncols=2,figsize=(8,8))
plt.suptitle(u'Lasso Shooting Algorithm Example',fontsize = 18) #用中文会出错，不知为何
plt.subplots_adjust(wspace = 0.25,hspace=0.25)
lambds = [0.05,3.5,50,100]
axes = axes.flatten()

for i in range(4):
    lambd = lambds[i]
    numIt = 600 #迭代次数
    wlog = np.zeros((numIt,M)) #记录weights的变化
    weights = np.zeros(M) #系数向量

    XX2 = 2*np.dot(datas.transpose(),datas)
    XY2 = 2*np.dot(datas.transpose(),values)
    for it in range(numIt):
        for k in range(M):
            ck = XY2[k]-np.dot(XX2[k,:],weights)+XX2[k,k]*weights[k]
            ak = XX2[k,k]
            #print ck,lambd
            if ck < -lambd:
                weights[k] = (ck+lambd)/ak
            elif ck > lambd:
                weights[k] = (ck-lambd)/ak
            else:
                weights[k] = 0
        wlog[it,:] = weights[:]
    ax = axes[i]
    for m in range(M):
        ax.plot(wlog[:,m])  
    ax.set_title('lambda='+np.str(lambd),{'fontname':'STFangsong','fontsize':10})
    ax.set_xlabel(u'迭代次数',{'fontname':'STFangsong','fontsize':10})
    ax.set_ylabel(u'各权值系数',{'fontname':'STFangsong','fontsize':10})   
savefig('lasso2.png',dpi=300,bbox_inches='tight')

L1 vs L2

岭回归正则化项是 L2 约束，而lasso的正则化项是 L1 约束。
下表展示了 L1,L2 的区别。

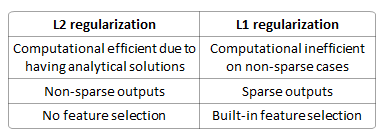
L1 具有的特征选择(稀疏性)的作用可以用下图来解释：
左侧的正方形表示 L1 约束，等高线图先与正方形的角上的点相切的可能性大，这时 β1=0 ， β2≠0 ，这起到了选择特征的目的；右侧的圆形表示 L2 约束，等高线图与圆上任一点相切的概率相同，故起不到特征选择的效果。