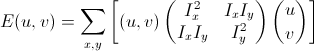Harris角点检测原理及openCV实现



本文转自：http://blog.csdn.net/next9pm/article/details/25345115

理论：

“如果某一点在任意方向的一个微小变动都会引起灰度很大的变化，那么我们就把它称之为角点”

 

由上面定义，我们可以想到算法思路：去检测图像像素的灰度变化情况，即求解　　

，其中，I(x,y)表示像素的灰度值

对于上式，我们希望找到使E的值尽量大的点，则，将上式右边泰勒展开得：

整理可得：

，进而可以表示为下式

这里考虑进去窗函数，设

于是，Harris整理出Harris算子的公式：

，其中M即为上面的矩阵，但是为什么会有这个算子呢，我试着给一点解释。

让我们来重新来考虑矩阵，一切的问题还得回归到数学上去

，这个矩阵先摆在这里，我们先看一下协方差矩阵。

　　协方差矩阵的作用为什么比方差和均值要大呢？显而易见方差和均值只是一维随机变量的统计值，而协方差就不一样了，它可以表示多维随机变量之间的相关性信息。协方差矩阵的一个很出色的应用就是在PCA中，选择主方向。协方差矩阵的对角线的元素表示的是各个维度的方差，而非对角线上的元素表示的是各个维度之间的相关性，因此，在PCA中，我们尽量将非对角线上的元素化为0，即将矩阵对角化，选特征值较大的维度，去掉特征值较小的维度，来获得主方向，并且使主方向与其他方向的相关性尽量小。那现在看看这个矩阵M,通过上面对协方差的描述，我们完全可以把这个矩阵看做一个二维随机分布的协方差矩阵，那么我们要做的就是将其对角化，求矩阵的两个特征值，然后根据这两个特征值来判断是不是角点（两个特征值都大代表角点）。

而对于Harris算子来说，我们也可以写成下式的形式：

，单单从这个式子中我们无法与上面联系起来，上面是说要让两个特征值都大的点，而这个式子是要求使R最大的点，而也没有办法一眼看出R与两个特征值之间的单调性关系。

下面我只是去验证此式的正确性，至于它到底是根据什么构造的，我还不清楚，如果有人知道，请告诉我一下~~

我们这里设，进而可以设，所以,现在我们对求导，整理后可得下式：

，对于k值，我们一般取0.04~0.06，所以对于角点，导数是正的，且随着特征值的增大，导数呈上升的趋势。也就是说这个算子是符合上面的理论分析的。

 

像上面这样去求解原则上是没有问题的，可是，众所周知，原始的Harris角点检测算法不具有尺度不变性（也就是说如果图像的尺度发生变化，那么可能原来是角点的点在新的尺度就不是角点了）。

所以，我们在进行运算的开始先将图像转化到尺度空间表示，即将原图像进行尺度变换，而尺度变换的方式就是问题的输入信号与尺度核函数做卷积运算：

，其中这里的运算为卷积运算，不是乘运算。即

，其中sigma表示尺度。然后，我们就使用L代替原图像去进行运算，而尺度成了我们运算的参数了。

我们知道Harris角点本身就不受光照，旋转的影响，现在我们又使其满足尺度不变性，所以，Harris角点可以作为一个优秀的特征来帮助我们解决问题。

<span style="font-size: 12px;">%Matlab 角点检测程序Harris

ori_im2 = rgb2gray(imread('test.jpg'));

fx = [5 0 -5; 8 0 -8; 5 0 -5];              % la gaucienne, ver axe x
Ix = filter2(fx, ori_im2);                  % la convolution vers axe x
fy = [5 8 5; 0 0 0; -5 -8 -5];              % la gaucienne, ver axe y
Iy = filter2(fy, ori_im2);

Ix2 = Ix.^2;
Iy2 = Iy.^2;
Ixy = Ix.*Iy;
clear Ix Iy;

h = fspecial('gaussian', [3 3], 2);         % générer une fonction gaussienne，sigma=2

Ix2 = filter2(h, Ix2);
Iy2 = filter2(h, Iy2);
Ixy = filter2(h, Ixy);

[height, width] = size(ori_im2);
result = zeros(height, width);              % enregistrer la position du coin

R = zeros(height, width);

k = 0.04;
Rmax = 0;                                   % chercher la valeur maximale de R

for i = 1:height
    for j = 1:width
        M = [Ix2(i,j) Ixy(i,j);Ixy(i,j) Iy2(i,j)];
        R(i,j) = det(M) - k*(trace(M))^2;
        if R(i,j) > Rmax
            Rmax = R(i,j);
        end
    end
end

cnt = 0;
for i = 2:height-1
    for j = 2:width-1
        % réduire des valuers minimales ，la taille de fenetre 3*3
        if R(i,j) > 0.01*Rmax && R(i,j) > R(i-1, j-1) && R(i,j) > R(i-1, j) ...
            && R(i,j) > R(i-1, j+1) && R(i,j) > R(i, j-1) && R(i,j) > R(i, j+1) ...
            && R(i,j) > R(i+1, j-1) && R(i,j) > R(i+1, j) && R(i,j) > R(i+1, j+1)
            result(i,j) = 1;
            cnt = cnt + 1;
        end
    end
end

[posr2, posc2] = find(result == 1);
cnt                                     % compter des coins
figure
imshow(ori_im2);
hold on;
plot(posc2, posr2, 'w*');
</span>

<span style="font-size: 12px;">%Matlab 角点检测程序Harris

ori_im2 = rgb2gray(imread('test.jpg'));

fx = [5 0 -5; 8 0 -8; 5 0 -5];              % la gaucienne, ver axe x
Ix = filter2(fx, ori_im2);                  % la convolution vers axe x
fy = [5 8 5; 0 0 0; -5 -8 -5];              % la gaucienne, ver axe y
Iy = filter2(fy, ori_im2);

Ix2 = Ix.^2;
Iy2 = Iy.^2;
Ixy = Ix.*Iy;
clear Ix Iy;

h = fspecial('gaussian', [3 3], 2);         % générer une fonction gaussienne，sigma=2

Ix2 = filter2(h, Ix2);
Iy2 = filter2(h, Iy2);
Ixy = filter2(h, Ixy);

[height, width] = size(ori_im2);
result = zeros(height, width);              % enregistrer la position du coin

R = zeros(height, width);

k = 0.04;
Rmax = 0;                                   % chercher la valeur maximale de R

for i = 1:height
    for j = 1:width
        M = [Ix2(i,j) Ixy(i,j);Ixy(i,j) Iy2(i,j)];
        R(i,j) = det(M) - k*(trace(M))^2;
        if R(i,j) > Rmax
            Rmax = R(i,j);
        end
    end
end

cnt = 0;
for i = 2:height-1
    for j = 2:width-1
        % réduire des valuers minimales ，la taille de fenetre 3*3
        if R(i,j) > 0.01*Rmax && R(i,j) > R(i-1, j-1) && R(i,j) > R(i-1, j) ...
            && R(i,j) > R(i-1, j+1) && R(i,j) > R(i, j-1) && R(i,j) > R(i, j+1) ...
            && R(i,j) > R(i+1, j-1) && R(i,j) > R(i+1, j) && R(i,j) > R(i+1, j+1)
            result(i,j) = 1;
            cnt = cnt + 1;
        end
    end
end

[posr2, posc2] = find(result == 1);
cnt                                     % compter des coins
figure
imshow(ori_im2);
hold on;
plot(posc2, posr2, 'w*');
</span>

优化后的角点检测

<span style="font-size: 12px;">%%% 时间优化--相邻像素用取差的方法

clear;
Image = imread('test.jpg');
Image = im2uint8(rgb2gray(Image));

dx = [-1 0 1; -1 0 1; -1 0 1];  % dx: 横向Prewitt查分模板
Ix2 = filter2(dx, Image).^2;
Iy2 = filter2(dx', Image).^2;
Ixy = filter2(dx, Image).*filter2(dx', Image);

%生成9*9高斯窗口。窗口越大，探测到的焦点越少。
h = fspecial('gaussian', 9, 2);
A = filter2(h, Ix2);    %用高斯窗口查分Ix2得到A
B = filter2(h, Iy2);
C = filter2(h, Ixy);

nrow = size(Image, 1);
ncol = size(Image, 2);
Corner = zeros(nrow, ncol); %矩阵Corner用来保存候选焦点位置，初值全0，值为1的点是角点
                            %真正的角点在117行由（row_ave，col_ave）得到
%参数t：点（i，j）八邻域的“相似度”参数，只有中心点与邻域其他八个点的像素值之差在
%（-t，+t）之间，才确认它们为相似点，相似点不在候选点之列
t = 20;

boundary = 8;
for i = boundary:nrow-boundary+1
    for j = boundary:ncol-boundary+1
        nlike = 0;  %相似点个数
        if Image(i-1,j-1) > Image(i,j)-t && Image(i-1,j-1) < Image(i,j)+t;
            nlike = nlike + 1;
        end
        if Image(i-1,j) > Image(i,j)-t && Image(i-1,j) < Image(i,j)+t
            nlike = nlike + 1;
        end
        if Image(i-1,j+1) > Image(i,j)-t && Image(i-1,j+1) < Image(i,j)+t
            nlike = nlike + 1;
        end
        if Image(i,j+1) > Image(i,j)-t && Image(i,j+1) < Image(i,j)+t
            nlike = nlike + 1;
        end
        if Image(i,j-1) > Image(i,j)-t && Image(i,j-1) < Image(i,j)+t
            nlike = nlike + 1;
        end
        if Image(i+1,j-1) > Image(i,j)-t && Image(i+1,j-1) < Image(i,j)+t
            nlike = nlike + 1;
        end
        if Image(i+1,j) > Image(i,j)-t && Image(i+1,j) < Image(i,j)+t
            nlike = nlike + 1;
        end
        if Image(i+1,j+1) > Image(i,j)-t && Image(i+1,j+1) < Image(i,j)+t
            nlike = nlike + 1;
        end
        if nlike>=2 && nlike<=6
            Corner(i,j) = 1;%如果周围有0,1,7,8个与中心相似的（i，j）
                            %那（i，j）就不是角点，所以，直接忽略
        end
    end
end

CRF = zeros(nrow, ncol);
CRFmax = 0;
t = 0.05;

for i = boundary:nrow-boundary+1
    for j = boundary:ncol-boundary+1
        if Corner(i,j) == 1
            M = [A(i,j) C(i,j); C(i,j) B(i,j)];
            CRF(i,j) = det(M) - t*(trace(M))^2;
            if CRF(i,j) > CRFmax
                CRFmax = CRF(i,j);
            end
        end
    end
end

count = 0;
t = 0.01;

for i = boundary:nrow-boundary+1
    for j = boundary:ncol-boundary+1
        if Corner(i,j) == 1
            if CRF(i,j) > t*CRFmax && CRF(i,j) > CRF(i-1, j-1) && CRF(i,j) > CRF(i-1, j) ...
            && CRF(i,j) > CRF(i-1, j+1) && CRF(i,j) > CRF(i, j-1) && CRF(i,j) > CRF(i, j+1) ...
            && CRF(i,j) > CRF(i+1, j-1) && CRF(i,j) > CRF(i+1, j) && CRF(i,j) > CRF(i+1, j+1)
                count = count + 1;
            else
                Corner(i,j) = 0;
            end
        end
    end
end

disp('角点个数');

count

figure,imshow(Image);
hold on;
for i = boundary:nrow-boundary+1
    for j = boundary:ncol-boundary+1
        col_ave = 0;
        row_ave = 0;
        k = 0;
        if Corner(i,j) == 1
            for x = i-3:i+3
                for y = j-3:j+3
                    if Corner(x,y) == 1
                        row_ave = row_ave + x;
                        col_ave = col_ave + y;
                        k = k + 1;
                    end
                end
            end
        end
        if k > 0
            plot(col_ave/k, row_ave/k, 'g.');
        end
    end
end</span>