【默慈金数+高精度】HDU3723Delta Wave【未AC】
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3723
Problem Description
A delta wave is a high amplitude brain wave in humans with a frequency of 1 – 4 hertz which can be recorded with an electroencephalogram (EEG) and is usually associated with slow-wave sleep (SWS).
-- from Wikipedia
The researchers have discovered a new kind of species called "otaku", whose brain waves are rather strange. The delta wave of an otaku's brain can be approximated by a polygonal line in the 2D coordinate system. The line is a route from point (0, 0) to (N, 0), and it is allowed to move only to the right (up, down or straight) at every step. And during the whole moving, it is not allowed to dip below the y = 0 axis.
For example, there are the 9 kinds of delta waves for N = 4:
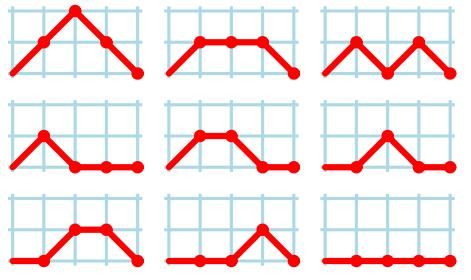
Given N, you are requested to find out how many kinds of different delta waves of otaku.
-- from Wikipedia
The researchers have discovered a new kind of species called "otaku", whose brain waves are rather strange. The delta wave of an otaku's brain can be approximated by a polygonal line in the 2D coordinate system. The line is a route from point (0, 0) to (N, 0), and it is allowed to move only to the right (up, down or straight) at every step. And during the whole moving, it is not allowed to dip below the y = 0 axis.
For example, there are the 9 kinds of delta waves for N = 4:

Given N, you are requested to find out how many kinds of different delta waves of otaku.
Input
There are no more than 20 test cases. There is only one line for each case, containing an integer N (2 < N <= 10000)
Output
Output one line for each test case. For the answer may be quite huge, you need only output the answer module 10
100.
Sample Input
3 4
Sample Output
4 9
代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<algorithm>
using namespace std;
const int N=10100; // 最大位数;
// 高精度加法;
string add(string aa,string bb)
{
string ans="";
int a[N]={0},b[N]={0};
int aLen=aa.size();
int bLen=bb.size();
for(int i=aLen-1;i>=0;i--)
a[aLen-i-1]=aa[i]-'0';
for(int i=bLen-1;i>=0;i--)
b[bLen-i-1]=bb[i]-'0';
int MaxLen=max(aLen,bLen);
for(int i=0;i<MaxLen;i++){
a[i]+=b[i];
a[i+1]+=a[i]/10;
a[i]%=10;
}
if(a[MaxLen]) MaxLen++;
for(int i=MaxLen-1;i>=0;i--) ans+=a[i]+'0';
return ans;
}
// 高精度减法; 保证aa>bb;
string sub(string aa,string bb)
{
string ans="";
int a[N]={0},b[N]={0};
int aLen=aa.size(),bLen=bb.size();
for(int i=0;i<aLen;i++)
a[aLen-i-1]=aa[i]-'0';
for(int i=0;i<bLen;i++)
b[bLen-i-1]=bb[i]-'0';
for(int i=0;i<aLen;i++){
a[i]-=b[i];
if(a[i]<0){
a[i+1]--;
a[i]+=10;
}
}
int MaxLen=aLen-1;
while(a[MaxLen]==0&&MaxLen) MaxLen--;
for(int i=MaxLen;i>=0;i--)
ans+=a[i]+'0';
return ans;
}
// 高精度乘以高精度;
string mul(string aa,string bb)
{
string ans="";
int a[N]={0},b[N]={0},c[N]={0};
int aLen=aa.size();
int bLen=bb.size();
for(int i=aLen-1;i>=0;i--)
a[aLen-1-i]=aa[i]-'0';
for(int i=bLen-1;i>=0;i--)
b[bLen-1-i]=bb[i]-'0';
for(int i=0;i<aLen;i++)
for(int j=0;j<bLen;j++)
c[i+j]+=a[i]*b[j];
for(int i=0;i<aLen+bLen;i++){
c[i+1]+=c[i]/10;
c[i]%=10;
}
int MaxLen=aLen+bLen;
while(c[MaxLen]==0) MaxLen--;
for(int i=MaxLen;i>=0;i--) ans+=c[i]+'0';
return ans;
}
// 高精度乘以单精度;
string mul_LL(string aa,long long b)
{
string ans="";
int a[N]={0};
int aLen=aa.size();
for(int i=0;i<aLen;i++)
a[aLen-i-1]=aa[i]-'0';
long long w=0;
for(int i=0;i<aLen;i++){
a[i]=a[i]*b+w;
w=a[i]/10;
a[i]%=10;
}
int MaxLen=aLen;
while(w){
a[MaxLen++]=w%10;
w/=10;
}
for(int i=MaxLen-1;i>=0;i--)
ans+=a[i]+'0';
return ans;
}
// 高精度除以高精度; aa/bb; s_v的值为1表示返回余数,为0表示返回商;
string div(string aa,string bb,int s_v)
{
string s="",v=""; // 存商,存余数;
int a[N]={0},b[N]={0},c[N]={0};
int aLen=aa.size();
int bLen=bb.size();
for(int i=0;i<aLen;i++)
a[aLen-i-1]=aa[i]-'0';
for(int i=0;i<bLen;i++)
b[bLen-i-1]=bb[i]-'0';
if(aLen<bLen||(aLen==bLen&&aa<bb)){
v=aa;
s="0";
if(s_v) return v; // 返回余数;
else return s;
}
int t=aLen-bLen; // 除数与被除数相差的位数;
for(int i=0;i<t;i++) bb+="0"; // 将除数bb扩大10^t倍;
for(int j=0;j<=t;j++){ // 商最多有t+1位;
while(1){
if((aa.size()>bb.size())||(aa.size()==bb.size()&&aa>=bb)){
aa=sub(aa,bb);
c[t-j]++;
}else{
bb=bb.substr(0,bb.size()-1);
break;
}
}
}
int MaxLen=aLen;
while(c[MaxLen]==0) MaxLen--;
for(int i=MaxLen;i>=0;i--)
s+=c[i]+'0';
v=aa;
if(s_v) return v;
else return s;
}
// 高精度除以单精度;
string div_LL(string aa,long long bb)
{
string ans="";
int aLen=aa.size();
if(aa=="0") return aa;
long long d=0;
for(int i=0;i<aLen;i++){
ans+=(d*10+(aa[i]-'0'))/bb+'0'; // 商;
d=(d*10+(aa[i]-'0'))%bb; // 余数;
}
int p=0;
int MaxLen=ans.size();
for(int i=0;i<MaxLen;i++)
if(ans[i]!='0'){
p=i;
break;
}
return ans.substr(p);
}
// 将一个long long 数据转换成string类型;
string exchang(long long a)
{
string ans="";
while(a){
ans+=a%10+'0';
a/=10;
}
reverse(ans.begin(),ans.end());
return ans;
}
/*
默慈金数和卡特兰数的关系;
T[k]=C(n,2*k)*h(k); 其中h(k),表示卡特兰数;
公式:sum(n)=T[0]+...T[m];其中m*2<=n;
T[k]=(n-2*k+1)*(n-2*k+2)/(k*(k+1))*T[k-1];
显然T[0]=1;
*/
string h[10010];
string H(int n)
{
string T[10010];
T[0]="1";
string sum="1";
for(int i=1;i+i<=n;i++){
long long tmp=(n-2*i+1)*(n-2*i+2);
long long tmp2=i*(i+1);
//T[i]=mul(exchang(tmp),T[i-1]);
T[i]=mul_LL(T[i-1],tmp); // O(n);n为字符串长度;
//T[i]=div(T[i],exchang(tmp2),0);
T[i]=div_LL(T[i],tmp2); // O(n);n为字符串长度;
sum=add(sum,T[i]); // O(n);
}
/*string mod="1";
for(int i=0;i<100;i++) mod+="0";
return div(sum,mod,1);
// 对10^100去模,
//2390662653430600799292157231322691445940220885813937208291336238647899820465455047642711310413072602
//6931034666534175155289953905326098910534128693214689917140093377138459245912955193770266157466468457
/*/
int p=0;
for(int i=0;i<sum.size();i++)
if(sum[i]!='0'){
p=i;
break;
}
return sum.substr(p,100-p);
}
int main()
{
int n;
cin.sync_with_stdio(false);
while(cin>>n){
if(h[n]!=""){
cout<<h[n]<<endl;
continue;
}
h[n]=H(n);
cout<<h[n]<<endl;
}
return 0;
}
Problem Description
A delta wave is a high amplitude brain wave in humans with a frequency of 1 – 4 hertz which can be recorded with an electroencephalogram (EEG) and is usually associated with slow-wave sleep (SWS).
-- from Wikipedia
The researchers have discovered a new kind of species called "otaku", whose brain waves are rather strange. The delta wave of an otaku's brain can be approximated by a polygonal line in the 2D coordinate system. The line is a route from point (0, 0) to (N, 0), and it is allowed to move only to the right (up, down or straight) at every step. And during the whole moving, it is not allowed to dip below the y = 0 axis.
For example, there are the 9 kinds of delta waves for N = 4:

Given N, you are requested to find out how many kinds of different delta waves of otaku.
-- from Wikipedia
The researchers have discovered a new kind of species called "otaku", whose brain waves are rather strange. The delta wave of an otaku's brain can be approximated by a polygonal line in the 2D coordinate system. The line is a route from point (0, 0) to (N, 0), and it is allowed to move only to the right (up, down or straight) at every step. And during the whole moving, it is not allowed to dip below the y = 0 axis.
For example, there are the 9 kinds of delta waves for N = 4:

Given N, you are requested to find out how many kinds of different delta waves of otaku.
Input
There are no more than 20 test cases. There is only one line for each case, containing an integer N (2 < N <= 10000)
Output
Output one line for each test case. For the answer may be quite huge, you need only output the answer module 10
100.
Sample Input
3
4
Sample Output
4
9