快速排序的划分算法的总结和思考
关于快速排序,它的关键点就在于划分算法,基本上有两种思路。
第一种是算法导论的解法,这种比较好理解,搜索一遍,找到比r小的元素然后调换位置, 并且i++。
第2种思路就比较难理解一点了,可以用一个数组进行比较。
设置两个指针,先从右向左遍历,找到比划分元小的数,然后调换位置;
再从左向右遍历,找到比划分元大的数,再和划分元调换位置。
如此循环直到,l>r为止。
int Partition3(int *a, int left, int right)
{
int pivot = a[right];
int tmp=a[right];
//这里是一个关键点,下面的while循环会改变a[right]的值,所以要用变量保存a[right]初值
while (left < right){
while (left < right && a[left] <= pivot){
left++;
}
a[right] = a[left];
while (left < right && a[right] >= pivot){
right--;
}
a[left] = a[right];
}
a[right]=tmp;
return right;
}
似乎感觉第2种应该会快一点,然而实际上,它们从时间复杂度来看,没有任何区别,都是O(n)的算法。
一会,通过下面的代码实际运行结果也可以清晰的看到。
关于快速排序,我觉得还有个重点就是是否使用随机数来确定划分元的位置。
刚开始学快排的时候,我总认为当数据量比较大的时候,随机化算法肯定是优于一般算法的。
在我们考虑,最坏情况下(即数组本来就是有序的),确实如此。
每次取最后一个元素的时候,这个时候生成的树会很深,因为每次都是1和n-1的划分。
时间复杂度接近0(n^2)。这个时候随机化算法才有巨大的提升!
#include <iostream>
#include <cstdio>
#include <ctime>
#include <time.h>
#include <cstdlib>
using namespace std;
#define MAX 30000
int randomRange(int a,int b){
return (int)((double)rand()/(double)RAND_MAX*(b-a+1)+a);
}
int Partition1(int *a,int left,int right)
{
int pivot=a[right];
int i=left-1,j;
for(j=left;j<right;++j){
if(a[j]<pivot){
i++;
swap(a[i],a[j]);
}
}
swap(a[i+1],a[right]);
return i+1;
}
int Partition2(int *a, int left, int right)
{
int t=randomRange(left,right);
swap(a[t],a[right]);
int pivot=a[right];
int i=left-1,j;
for(j=left;j<right;++j){
if(a[j]<pivot){
i++;
swap(a[i],a[j]);
}
}
swap(a[i+1],a[right]);
return i+1;
}
int Partition3(int *a, int left, int right)
{
int pivot = a[right];
int tmp=a[right];
//这里是一个关键点,下面的while循环会改变a[right]的值,所以要用变量保存a[right]初值
while (left < right){
while (left < right && a[left] <= pivot){
left++;
}
a[right] = a[left];
while (left < right && a[right] >= pivot){
right--;
}
a[left] = a[right];
}
a[right]=tmp;
return right;
}
int Partition4(int *a, int left, int right)
{
int t=randomRange(left,right);
int pivot = a[t];
//而这里就不需要tmp作为变量保存初值了,因为下面是直接交换的。而不是partition3写法的直接覆盖
while (left < right){
while (left < right && a[right] >= pivot){
right--;
}
swap(a[t],a[right]);
t=right;
while (left < right && a[left] <= pivot){
left++;
}
swap(a[t],a[left]);
t=left;
}
return left;
}
void quickSort1(int *a, int left, int right){
if (left < right){
int pivot = Partition1(a, left, right);
quickSort1(a, left, pivot-1);
quickSort1(a, pivot+1, right);
}
}
void quickSort2(int *a, int left, int right){
if (left < right){
int pivot = Partition2(a, left, right);
quickSort2(a, left, pivot-1);
quickSort2(a, pivot+1, right);
}
}
void quickSort3(int *a, int left, int right){
if (left < right){
int pivot = Partition3(a, left, right);
quickSort1(a, left, pivot-1);
quickSort1(a, pivot+1, right);
}
}
void quickSort4(int *a, int left, int right){
if (left < right){
int pivot = Partition4(a, left, right);
quickSort2(a, left, pivot-1);
quickSort2(a, pivot+1, right);
}
}
int main(void)
{
int a[MAX] = {0};
int i;
clock_t start,finish;
srand(time(NULL));
printf("算法导论的划分算法:\n");
for (i=0; i<MAX; i++){
// a[i] = rand()%100;
a[i]=i;
}
start=clock();
quickSort1(a, 0, MAX-1);
finish=clock();
cout <<"最后一个元素作为划分的时间 :"<<finish-start << "/" << CLOCKS_PER_SEC << " (s) "<< endl;
for (i=0; i<MAX; i++){
// a[i] = rand()%100;
a[i]=i;
}
start=clock();
quickSort2(a, 0, MAX-1);
finish=clock();
cout <<"取随机数作为划分的时间 :"<<finish-start << "/" << CLOCKS_PER_SEC << " (s) "<< endl<<endl;
printf("另一种划分算法:\n");
for (i=0; i<MAX; i++){
a[i] = i;
}
start=clock();
quickSort3(a, 0, MAX-1);
finish=clock();
cout <<"最后一个元素作为划分的时间 :"<<finish-start << "/" << CLOCKS_PER_SEC << " (s) "<< endl;
for (i=0; i<MAX; i++){
a[i] = i;
}
start=clock();
quickSort4(a, 0, MAX-1);
finish=clock();
cout <<"取随机数作为划分的时间 :"<<finish-start << "/" << CLOCKS_PER_SEC << " (s) "<< endl<<endl;
return 0;
}
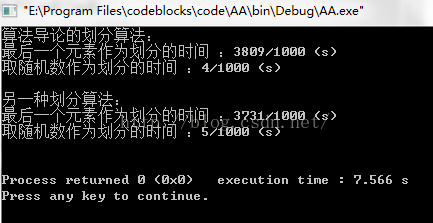
清晰的看到,时间的巨大的提升。
注意,这里的数组的大小MAX是30000,若再开大一点,一般的计算机最坏情况下就算不出来了。
上面这个数组是最坏情况,如果我们把数组的初始化改为:
for (i=0; i<MAX; i++){
a[i] = rand()%100;
}
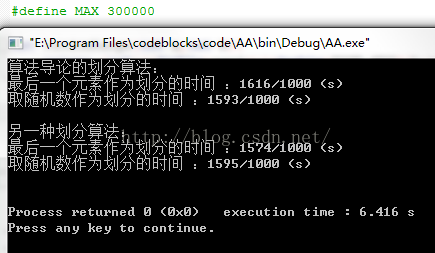
并且把数组的大小MAX改为300000,那么运行的结果是什么样的呢?
总结:随机化算法对于大量的随机数,即一般排序情况,几乎没有任何提升。
两种划分算法从时间复杂度来考虑也几乎没有任何区别。
最后想到,之前好像做过一个关于快排的题目,当时还没有做出来,去翻下了以前的博客果然有一个坑还没有填上。
题目为:
著名的快速排序算法里有一个经典的划分过程:我们通常采用某种方法取一个元素作为主元,通过交换,把比主元小的元素放到它的左边,比主元大的元素放到它的右边。 给定划分后的N个互不相同的正整数的排列,请问有多少个元素可能是划分前选取的主元?
例如给定N = 5, 排列是1、3、2、4、5。则:
因此,有3个元素可能是主元。
输入格式:
输入在第1行中给出一个正整数N(<= 105); 第2行是空格分隔的N个不同的正整数,每个数不超过109。
输出格式:
在第1行中输出有可能是主元的元素个数;在第2行中按递增顺序输出这些元素,其间以1个空格分隔,行末不得有多余空格。
输入样例:5 1 3 2 4 5输出样例:
3 1 4 5这个是浙大PAT的练习题。感觉这个题目还是挺好的,可以加深对快排的理解!
解题思路和代码:http://blog.csdn.net/a342500329a/article/details/48598561