HDU 2818 Building Block（带权并查集）

题目链接：Click here~~

题意：

给 n 块砖头，开始各为一堆，两种操作：

1、把 X 所在的那一堆放到 Y 所在的那一堆上面。

2、询问 X 下面有多少块砖。

解题思路：

好像大家都叫它带权并查集，那为了方便，这里也这样叫吧。

应该比较容易联想到用并查集吧，因为操作 1 又是关于两个集合的合并。

开始惯性思维，想着用集合的根代表这堆砖的顶部，发现 GG 了。

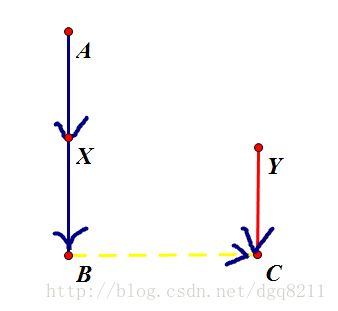
那我们尝试一下，如果用集合的根代表这堆砖的底部，能否处理这样的询问。先上个图。

图中箭头表示父亲的指向，这样说好像欠妥，其实有了路径压缩以后，每个节点存的前驱不再是父亲，而是祖先。

那为什么还会有一些节点指向了父亲而不是指向根呢？

是因为当这些节点的祖先指向其他节点的祖先时，并没有来得及更新它们。

而路径压缩的思想就是，先暂时舍弃这些更新，等到每次查找根的时候，把集合中的每个节点全都指向根，这样操作均摊的复杂度比较低。

————————————————————上面这段话完全是针对初学者来的啊，牛牪犇请无视———————————————————————

图中所示的操作是一种关于 X 移向 Y 的情况。

我们尝试维护一个 under[i] 数组，表示 i 下面有多少块砖。

当将 X 的根指向 Y 的根的时候，有 under[root(x)] = count[root(y)]。

所以，还需要再维护一个 count[i] 数组，表示以 i 为根的这个集合共有多少个节点。（这个很好维护，入门选手都可以。

可是我们难以避免的，会遇到上段话中提到的问题。

采用与路径压缩相似的思想，先暂时舍弃这些更新，等到每次查找根的时候，再去更新。也就是我们可以和路径压缩一起进行这个更新。

所以，under[i] 其实代表的只是从 i 下面到它当前所标记的根有多少块砖。

而 under[i] 的改变只会随着它当前所标记的那个根节点的改变而改变，而且每次改变后，新的根节点的 under[] 的值一定是 0。

从而更新可以直接写成 under[x] += under[old_root(x)] ，不过要保证 old_root(x) 已经得到更新，所以也要先递归。

#include <stdio.h>
#include <string.h>
#include <algorithm>

using namespace std;

const int N = 3e4 + 5;

namespace ufSet
{
    int pre[N], count[N], under[N];
    void init(){
        memset(under,0,sizeof(under));
        memset(pre,-1,sizeof(pre));
        fill(count,count+N,1);
    }
    int root(int u){
        int &fa = pre[u];
        if(fa == -1)
            return u;
        else
        {
            int rt = root(fa);
            under[u] += under[fa];
            return fa = rt;
        }
    }
    bool gather(int u,int v){
        int ru = root(u);
        int rv = root(v);
        if(ru == rv)
            return false;
        else
        {
            pre[ru] = rv;
            under[ru] = count[rv];
            count[rv] += count[ru];
            count[ru] = 0;
            return true;
        }
    }
}using namespace ufSet;

int main()
{
    int q;
    while(~scanf("%d",&q))
    {
        init();
        while(q--)
        {
            char op[4];
            int u,v;
            scanf("%s",op);
            if(op[0] == 'M')
            {
                scanf("%d%d",&u,&v);
                gather(u,v);
            }
            else
            {
                scanf("%d",&u);
                root(u);
                printf("%d\n",under[u]);
            }
        }
    }
    return 0;
}