最小生成树—— Prim算法 ▪ Kruskal算法C语言实现
在一给定的 无向图G = (V, E) 中,(u, v) 代表连接顶点 u 与顶点 v 的边(即),而 w(u, v) 代表此 边的权重,若存在 T 为 E 的 子集(即)且为无循环图,使得
的 w(T) 最小,则此 T 为 G 的
最小生成树。
最小生成树其实是
最小权重生成树的简称。
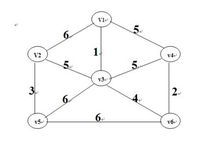
许多应用问题都是一个求无向连通图的最小生成树问题。例如:要在n个 城市之间铺设光缆,主要目标是要使这 n 个城市的任意两个之间都可以通信,但铺设光缆的费用很高,且各个城市之间铺设光缆的费用不同;另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。
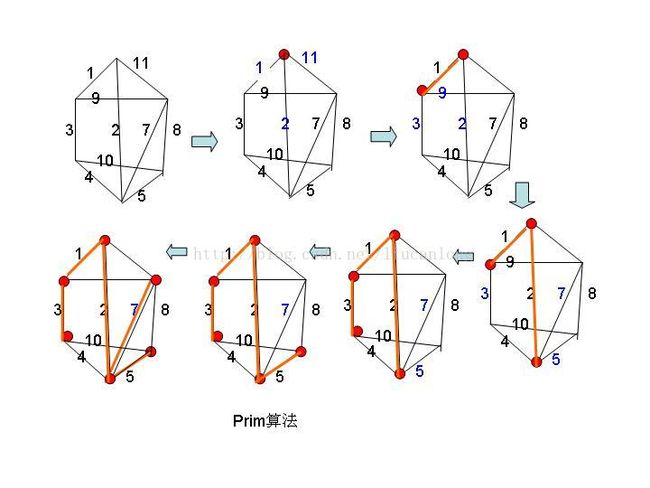
Prim算法
就是点优先,原始集合里面存放所有的点,目标集合最初为空,先任意从原始集合取一个点放在目标集合,此时开始搜索,原始集合到目标集合最近的一个点,找到后将他放入目标集合,更新原始集合中的点到目标集合的距离,一直将原始集合中的点全部加入到目标集合中,完成搜索。
#include<stdio.h>
int arr[101][101];
int main(){
int n,ttt = 0;
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
scanf("%d",&arr[i][j]);
}
}
for(int j=2;j<=n;j++){
int min = 100000000;
int index = 0;
for(int i=1;i<=n;i++){
if(arr[1][i]==0) continue;
if(arr[1][i]<min){
min = arr[1][i];
index = i;
}
}
ttt += arr[1][index];
for(int i=1;i<=n;i++){
arr[1][i] = arr[1][i]<arr[index][i]?arr[1][i]:arr[index][i];
}
}
printf("%d\n",ttt);
return 0;
}
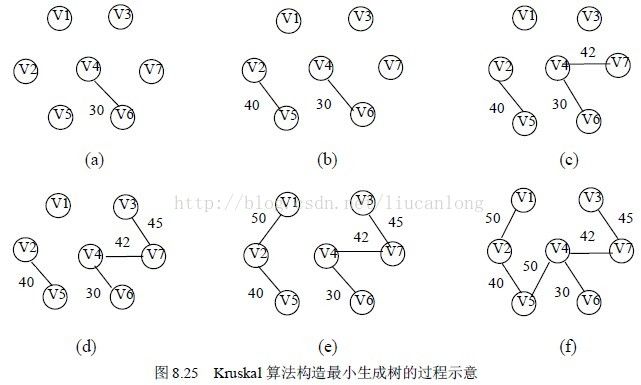
Kruskal算法
就是边优先,先将每一条边从大到小排序,每次去最小的一条边连接两个点,但是需要判断,是否形成回路。#include<iostream>
#include<stdio.h>
#include<cstdlib>
using namespace std;
struct eg{
int start;
int end;
int weight;
};
int addNum = 0;
eg arr[5060];
int cmp(const void *v1,const void *v2){
eg t1 = *(eg*)v1;
eg t2 = *(eg*)v2;
return t1.weight-t2.weight;
}
int main(){
int n,index=0,ttt;
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(j<=i){
scanf("%d",&ttt);
}else{
scanf("%d",&arr[index].weight);
arr[index].start = i;
arr[index].end = j;
index++;
}
}
}
int num = n*(n-1)/2;
qsort(arr,num,sizeof(eg),cmp);
int countW = 0;
int x[101];
for(int i=1;i<=100;i++){
x[i] = i;
}
for(int i=0;i<num&&addNum<n;i++){
int k,g;
for(k=arr[i].start;x[k]!=k;k=x[k]) //判断线段的起始点所在的集合
x[k]=x[x[k]];
for(g=arr[i].end;x[g]!=g;g=x[g]) //判断线段的终点所在的集合
x[g]=x[x[g]];
if(k!=g) //如果线段的两个端点所在的集合不一样
{
x[g]=k;
countW+=arr[i].weight;
addNum++;
//printf("最小生成树中加入边:%d %d/n",a[i].m,a[i].n);
}
}
printf("%d\n",countW);
return 0;
}
样例输入
4
0 4 9 21
4 0 8 17
9 8 0 16
21 17 16 0
样例输出
28