B-Tree和B+Tree

B-Tree

为了描述B-Tree，首先定义一条数据记录为一个二元组[key, data]，key为记录的键值，对于不同数据记录，key是互不相同的；data为数据记录除key外的数据。那么B-Tree是满足下列条件的数据结构：

d为大于1的一个正整数，称为B-Tree的度。

h为一个正整数，称为B-Tree的高度。

每个非叶子节点由n-1个key和n个指针组成，其中d<=n<=2d。

每个叶子节点最少包含一个key和两个指针，最多包含2d-1个key和2d个指针，叶节点的指针均为null 。

所有叶节点具有相同的深度，等于树高h。

key和指针互相间隔，节点两端是指针。

一个节点中的key从左到右非递减排列。

所有节点组成树结构。

每个指针要么为null，要么指向另外一个节点。

如果某个指针在节点node最左边且不为null，则其指向节点的所有key小于 v(key1) ，其中 v(key1) 为node的第一个key的值。

如果某个指针在节点node最右边且不为null，则其指向节点的所有key大于 v(keym) ，其中 v(keym) 为node的最后一个key的值。

如果某个指针在节点node的左右相邻key分别是 keyi 和 keyi+1 且不为null，则其指向节点的所有key小于 v(keyi+1) 且大于 v(keyi) 。

图2是一个d=2的B-Tree示意图。

图2

由于B-Tree的特性，在B-Tree中按key检索数据的算法非常直观：首先从根节点进行二分查找，如果找到则返回对应节点的data，否则对相应区间的指针指向的节点递归进行查找，直到找到节点或找到null指针，前者查找成功，后者查找失败。B-Tree上查找算法的伪代码如下：

BTree_Search(node, key) {
    if(node == null) return null;
    foreach(node.key)
    {
        if(node.key[i] == key) return node.data[i];
            if(node.key[i] > key) return BTree_Search(point[i]->node);
    }
    return BTree_Search(point[i+1]->node);
}
data = BTree_Search(root, my_key);

关于B-Tree有一系列有趣的性质，例如一个度为d的B-Tree，设其索引N个key， 则其树高h的上限为 logd((N+1)/2) ，检索一个key，其查找节点个数的渐进复杂度为 O(logdN) 。从这点可以看出，B-Tree是一个非常有效率的索引数据结构。

另外，由于插入删除新的数据记录会破坏B-Tree的性质，因此在插入删除时，需要对树进行一个分裂、合并、转移等操作以保持B-Tree性质.

The height of a B-Tree:

Number of disk accesses on a B-tree is often proportional to the B-tree height.

Theorem 18.1

If n ≥ 1 then h ≤ log_t (n + 1)/2                                                     Note:  log_2t n ≤ log_t n

for any n-keyB-Tree T of height h, and minimum degree t ≥ 2:

2t-1 is maximum number of keys

2t is the maximum number of children

t-1 is the minimum number of keys

t is the minimum number of children

Proof

By B-tree definition, root contains at least one key and all other nodes at least t-1 keys.

t-1 key node must have t children nodes.

Root has at least 1 key

• depth 0 root 1 node with at least 1 key
• depth 1 at least 2 nodes with at least t-1 keys
• depth 2 at least 2t nodes with at least t-1 keys
• depth 3 at least 2t² nodes with at least t-1 keys

  :

• depth h at least 2t^h-1 nodes

The number n of keys satisfies (by A. 5 of text):

• 1 is the root key
• t-1 is minimum keys per node of non-root nodes
• summation of total number of non-root nodes

 Theorem 18.1 Proof

n	≥ 2th-1
(n+1)/2	≥ th
th	≤ (n+1)/2
logt th	≤ logt (n+1)/2
h	≤ logt (n + 1)/2

Example

t = 2, n = 65536

h ≤ log₂ (65536 + 1)/2 = log₂ 32768 = log₂ 2¹⁵ = 15

t = 8, n = 65536

h ≤ log₈ (65536 + 1)/2 = log₈ 32768 = log₈ 8⁵ = 5

B+Tree

B-Tree有许多变种，其中最常见的是B+Tree，例如MySQL就普遍使用B+Tree实现其索引结构。

与B-Tree相比，B+Tree有以下不同点：

每个节点的指针上限为2d而不是2d+1。

内节点不存储data，只存储key；叶子节点不存储指针。

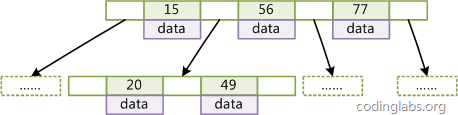
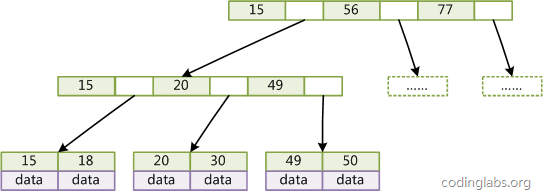
图3是一个简单的B+Tree示意。

图3

由于并不是所有节点都具有相同的域，因此B+Tree中叶节点和内节点一般大小不同。这点与B-Tree不同，虽然B-Tree中不同节点存放的key和指针可能数量不一致，但是每个节点的域和上限是一致的，所以在实现中B-Tree往往对每个节点申请同等大小的空间。

一般来说，B+Tree比B-Tree更适合实现外存储索引结构，具体原因与外存储器原理及计算机存取原理有关，将在下面讨论。

带有顺序访问指针的B+Tree

一般在数据库系统或文件系统中使用的B+Tree结构都在经典B+Tree的基础上进行了优化，增加了顺序访问指针(称为B* tree)。

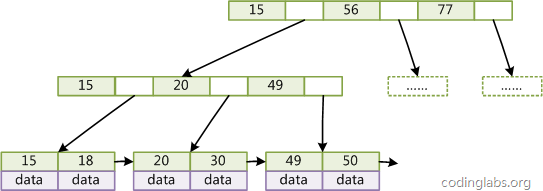
图4

如图4所示，在B+Tree的每个叶子节点增加一个指向相邻叶子节点的指针，就形成了带有顺序访问指针的B+Tree。做这个优化的目的是为了提高区间访问的性能，例如图4中如果要查询key为从18到49的所有数据记录，当找到18后，只需顺着节点和指针顺序遍历就可以一次性访问到所有数据节点，极大提到了区间查询效率。

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。

B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。

所以，B*树分配新结点的概率比B+树要低，空间使用率更高；