poj 1556 The Doors (建图+最短路)
|
The Doors
Description
You are to find the length of the shortest path through a chamber containing obstructing walls. The chamber will always have sides at x = 0, x = 10, y = 0, and y = 10. The initial and final points of the path are always (0, 5) and (10, 5). There will also be from 0 to 18 vertical walls inside the chamber, each with two doorways. The figure below illustrates such a chamber and also shows the path of minimal length.
Input
The input data for the illustrated chamber would appear as follows.
2 4 2 7 8 9 7 3 4.5 6 7 The first line contains the number of interior walls. Then there is a line for each such wall, containing five real numbers. The first number is the x coordinate of the wall (0 < x < 10), and the remaining four are the y coordinates of the ends of the doorways in that wall. The x coordinates of the walls are in increasing order, and within each line the y coordinates are in increasing order. The input file will contain at least one such set of data. The end of the data comes when the number of walls is -1. Output
The output should contain one line of output for each chamber. The line should contain the minimal path length rounded to two decimal places past the decimal point, and always showing the two decimal places past the decimal point. The line should contain no blanks.
Sample Input 1 5 4 6 7 8 2 4 2 7 8 9 7 3 4.5 6 7 -1 Sample Output 10.00 10.06 Source
Mid-Central USA 1996
|
思路：
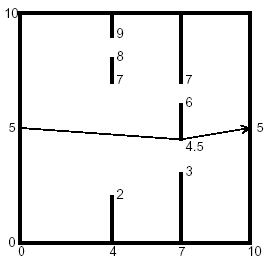
将一个门可以看成两个点，将所有点建图，如果两点能到达，则距离为坐标距离，不能到达则距离为INF。
ps：其他点是没有用的，这个可以根据三角形的两边之和大于第三边和两点之间线段最短证明。
代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#define maxn 105
using namespace std;
const int INF=0x3f3f3f3f;
int n,m,ans,dcnt,pcnt;
bool vis[maxn];
double dist[maxn];
double city[maxn][maxn];
struct Node
{
double x1,y1,y2;
} door[55]; // 开始开小了 WA了一次 一道墙有两个门
struct node
{
double x,y;
} point[maxn];
void init()
{
int i,j;
for(i=1; i<=80; i++)
{
dist[i]=INF;
for(j=1; j<=80; j++)
{
city[i][j]=INF;
}
}
memset(vis,0,sizeof(vis));
}
void Dijkstra()
{
int i,j,mi,k,now=1;
vis[1]=1;
dist[1]=0;
n=pcnt;
for(i=1; i<n; i++)
{
for(j=1; j<=n; j++)
{
if(!vis[j]&&city[now][j]+dist[now]<dist[j])
dist[j]=city[now][j]+dist[now];
}
mi=INF;
for(j=1; j<=n; j++)
{
if(!vis[j]&&dist[j]<mi)
{
mi=dist[j];
k=j;
}
}
now=k;
if(k==n) break ;
vis[k]=1;
}
}
bool isok(int k1,int k2) // 判断两点之间能否到达
{
int i,j;
double k,x,y,xx1,yy1,xx2,yy2;
xx1=point[k1].x;
yy1=point[k1].y;
xx2=point[k2].x;
yy2=point[k2].y;
k=(yy2-yy1)/(xx2-xx1);
for(i=1; i<=dcnt; i+=2)
{
if(door[i].x1<=xx1) continue ;
if(door[i].x1>=xx2) break ;
x=door[i].x1;
y=yy1+k*(x-xx1);
if(!(y>=door[i].y1&&y<=door[i].y2||y>=door[i+1].y1&&y<=door[i+1].y2)) return false ;
}
return true ;
}
double caldist(int k1,int k2) // 计算两点之间的距离
{
double xx,yy;
xx=(point[k1].x-point[k2].x);
yy=(point[k1].y-point[k2].y);
return sqrt(xx*xx+yy*yy);
}
void buildgraph() // 建图
{
int i,j;
for(i=1; i<=pcnt; i++)
{
for(j=i+1; j<=pcnt; j++)
{
if(point[i].x==point[j].x) continue ;
if(isok(i,j)) city[i][j]=city[j][i]=caldist(i,j);
}
}
}
int main()
{
int i,j;
double x1,y1,y2,yy1,yy2;
while(scanf("%d",&n),n!=-1)
{
init();
dcnt=pcnt=0;
pcnt++;
point[pcnt].x=0;
point[pcnt].y=5;
for(i=1; i<=n; i++) // 加door 加point
{
scanf("%lf%lf%lf%lf%lf",&x1,&y1,&y2,&yy1,&yy2);
dcnt++;
door[dcnt].x1=door[dcnt+1].x1=x1;
door[dcnt].y1=y1;
door[dcnt].y2=y2;
dcnt++;
door[dcnt].y1=yy1;
door[dcnt].y2=yy2;
pcnt++;
point[pcnt].x=x1;
point[pcnt].y=y1;
pcnt++;
point[pcnt].x=x1;
point[pcnt].y=y2;
pcnt++;
point[pcnt].x=x1;
point[pcnt].y=yy1;
pcnt++;
point[pcnt].x=x1;
point[pcnt].y=yy2;
}
pcnt++;
point[pcnt].x=10;
point[pcnt].y=5;
buildgraph();
Dijkstra();
printf("%.2f\n",dist[n]);
}
return 0;
}