LCA转RMQ 模版及解析 + LCA倍增法模版
九野的博客,转载请注明出处:http://blog.csdn.net/acmmmm/article/details/15490519
LCA: 最近公共祖先
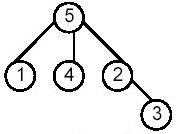
所谓最近公共祖先,是针对一棵树上的任意2个不同节点来说的。
则 LCA(2,3) = 2 ; LCA(3,4) = 5; LCA(1,2) = 5; LCA(1,5) = 5;
RMQ: 区间最值问题, 给定一组数,在O(logn) 的复杂度内回答区间的最值 (一般采用线段树 或 ST算法解决 ,这里采用ST算法解决,可以把复杂度降到O(1) )
ST算法:http://blog.csdn.net/acmmmm/article/details/15026475
LCA问题: 找到任意点的父节点(时常问题是给定树求任意点的最短路,对于任意点 u,v 答案为 ans = dis(u) + dis(v) - 2* dis( LCA(u,v) ) ,dis(u)表示u点与根节点的距离
对于无根树,在上述最短路问题中可直接转为有根树求解,不影响结果
图解LCA转RMQ:点击打开链接
LCA转RMQ:
对树从根节点开始 DFS
得到3个数组
int deep [N]; //第i个访问的结点的深度
int index[N]; //第i个访问的结点的编号
int first[N]; //第i个结点是第几个访问的
我们可以在DFS中加个时间戳(就是DFS的次数)time 来表示这是第几次访问
***在遍历完一个子节点要再扫一遍父节点 再遍历其子节点*** 保证父节点始终穿插在子节点中
如父节点为a 子节点为b1 b2 b3 则遍历顺序是 a -> b1 -> a -> b2 -> a -> b3 -> a
(DFS过程顺便也可以求出dis数组)
对于任意节点 u v 和其公共祖先 c = LCA(u, v)
很显然红字可以得出结论 :
先遍历u 再遍历 c 再遍历 v
那么在deep数组中的位置关系就是 [ u c v ]
这样:c 的深度一定是区间中最小的
问题就转化为:求区间最小值 -> 即 RMQ问题
用u v 求出deep中最小值,再用index数组得到最小值对应的点标
用first可以定位 区间范围,若求红字部分 LCA(a, b1) ,区间可以为 [a,b1] 也可以为[b1 a b2 a...]
所以只需用点第一次 出现位置 (first记录)即可。
注意:图可能不连通,即图为森林(众多的树)此时可以建一个虚根,把虚根和每个联通块之间连一条 权值为 inf 的边
(或指定1点为根,并查集把和1不在一个集合的联通块 建权值为inf 的边)
log() 是以e为底的!!!
LCA倍增法:
#include"cstdio"
#include"iostream"
#include"queue"
#include"algorithm"
#include"set"
#include"queue"
#include"cmath"
#include"string.h"
#include"vector"
using namespace std;
#define N 10050
struct Edge{
int from, to, dis, nex;
}edge[5*N];
int head[N],edgenum,dis[N],fa[N][20],dep[N]; //fa[i][x] 是i的第2^x个父亲(如果超过范围就是根)
void add(int u,int v,int w){
Edge E={u,v,w,head[u]};
edge[edgenum] = E;
head[u]=edgenum++;
}
void bfs(int root){
queue<int> q;
fa[root][0]=root;dep[root]=0;dis[root]=0;
q.push(root);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=1;i<20;i++)fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=head[u]; ~i;i=edge[i].nex){
int v=edge[i].to;if(v==fa[u][0])continue;
dep[v]=dep[u]+1;dis[v]=dis[u]+edge[i].dis;fa[v][0]=u;
q.push(v);
}
}
}
int Lca(int x,int y){
if(dep[x]<dep[y])swap(x,y);
for(int i=0;i<20;i++)if((dep[x]-dep[y])&(1<<i))x=fa[x][i];
if(x==y)return x;
for(int i=19;i>=0;i--)if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
void init(){memset(head, -1, sizeof head); edgenum = 0;}