hdoj 3879 Base Station 【最小割 之 最大权闭合图】
Base StationTime Limit: 5000/2000 MS (Java/Others) Memory Limit: 65768/32768 K (Java/Others)Total Submission(s): 2100 Accepted Submission(s): 885
Problem Description
A famous mobile communication company is planning to build a new set of base stations. According to the previous investigation, n places are chosen as the possible new locations to build those new stations. However, the condition of each position varies much, so the costs to built a station at different places are different. The cost to build a new station at the ith place is P
i (1<=i<=n).
When complete building, two places which both have stations can communicate with each other. Besides, according to the marketing department, the company has received m requirements. The ith requirement is represented by three integers A i, B i and C i, which means if place A i and B i can communicate with each other, the company will get C i profit. Now, the company wants to maximize the profits, so maybe just part of the possible locations will be chosen to build new stations. The boss wants to know the maximum profits.
Input
Multiple test cases (no more than 20), for each test case:
The first line has two integers n (0<n<=5000) and m (0<m<=50000). The second line has n integers, P1 through Pn, describes the cost of each location. Next m line, each line contains three integers, A i, B i and C i, describes the ith requirement.
Output
One integer each case, the maximum profit of the company.
Sample Input
Sample Output
|
题意:一个公司计划建N个基站,已给出建造每个基站所需要的成本。现在市场营销部收到M个请求,每个请求由3个整数a、b、c组成,表示若a基站和b基站可以相互联系则该公司会得到c的利润。问你该公司可以得到的最大收益。(并不一定要建造N个基站)
这里只详细说明建图,具体证明请看神级论文 受益匪浅
希望你已经看过上面的论文
分析:对于第i个请求,我们已经知道满足它的必要条件建造a基站和b基站,这也就意味着当第i个请求被满足的时候,那么基站a和基站b肯定已经建好了。我们把第i个请求和基站a、b各虚拟成一个点,则i -> a && i -> b是成立的。知道了这么多,我们就可以得到一个每个点都具有点权的有向图。
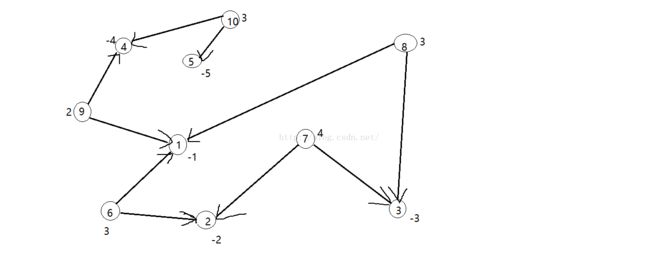
这里以标准输入为例,将第i个请求虚拟成点i+N,将第i个基站虚拟成点i。根据必要关系我们可以得到该图
图中每个点都具有点权,代表选择此点的收益。这样就将问题变成——求该图的最大权闭合图。
根据已经构建好的有向图——建新图:设置超级源点source,超级汇点sink
1,source向所有点权为正的点建边,容量为点权;
2,按图中所有边建图,容量为无穷大;
4,所有点权为负的点向sink建边, 容量为点权的绝对值。
统计出所有点权为正的点的权值之和sum,最后结果就是sum - 最小割。
AC代码:
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define MAXN 60000
#define MAXM 400000+10
#define INF 0x3f3f3f3f
using namespace std;
struct Edge
{
int from, to, cap, flow, next;
};
Edge edge[MAXM];
int head[MAXN], edgenum;
int dist[MAXN], cur[MAXN];
bool vis[MAXN];
int N, M;
void init()
{
edgenum = 0;
memset(head, -1, sizeof(head));
}
void addEdge(int u, int v, int w)
{
Edge E1 = {u, v, w, 0, head[u]};
edge[edgenum] = E1;
head[u] = edgenum++;
Edge E2 = {v, u, 0, 0, head[v]};
edge[edgenum] = E2;
head[v] = edgenum++;
}
int sum;//记录图中所有正权点 的权值之和
int source, sink;
void getMap()
{
int a, b, c;
source = 0, sink = N+M+1;
sum = 0;
for(int i = 1; i <= N; i++)
{
scanf("%d", &a);
//点权为负->收益是正的 它向汇点建边
addEdge(i, sink, a);
}
for(int i = 1; i <= M; i++)
{
scanf("%d%d%d", &a, &b, &c);
addEdge(i+N, a, INF);
addEdge(i+N, b, INF);
//点权为正->收益是正的 源点向它建边
addEdge(source, i+N, c), sum += c;
}
}
bool BFS(int s, int t)
{
queue<int> Q;
memset(dist, -1, sizeof(dist));
memset(vis, false, sizeof(vis));
dist[s] = 0;
vis[s] = true;
Q.push(s);
while(!Q.empty())
{
int u = Q.front();
Q.pop();
for(int i = head[u]; i != -1; i = edge[i].next)
{
Edge E = edge[i];
if(!vis[E.to] && E.cap > E.flow)
{
dist[E.to] = dist[u] + 1;
if(E.to == t) return true;
vis[E.to] = true;
Q.push(E.to);
}
}
}
return false;
}
int DFS(int x, int a, int t)
{
if(x == t || a == 0) return a;
int flow = 0, f;
for(int &i = cur[x]; i != -1; i = edge[i].next)
{
Edge &E = edge[i];
if(dist[E.to] == dist[x] + 1 && (f = DFS(E.to, min(a, E.cap-E.flow), t)) > 0)
{
edge[i].flow += f;
edge[i^1].flow -= f;
flow += f;
a -= f;
if(a == 0) break;
}
}
return flow;
}
int Maxflow(int s, int t)
{
int flow = 0;
while(BFS(s, t))
{
memcpy(cur, head, sizeof(head));
flow += DFS(s, INF, t);
}
return flow;
}
int main()
{
while(scanf("%d%d", &N, &M) != EOF)
{
init();
getMap();
printf("%d\n", sum - Maxflow(source, sink));
}
return 0;
}