约束条件下二次误差度量简化方法

上一章主要从场景可见性剔除、多分辨率模型简化、基于图像与GPU的加速绘制以及场景数据组织等方面介绍场景加速绘制的基本原理与方法。本章将首先介绍多分辨率模型简化部分中的二次误差度量方法，然后提出约束条件下的改进算法，最后完成模型简化实验。虽然此方法在预处理阶段完成，属于静态简化的范畴，但也是下一章将要介绍的动态简化方法的基础，在预处理阶段与实时运行阶段都可作为边折叠操作的基础。

3.1 引言

由于三维场景浏览和交互操作更贴近人们在现实环境中的观察方式和感受，以及虚拟仿真技术、图形技术、网络技术和数字城市技术的快速发展，对三维仿真应用的需求越来越大。而通过建模工具生成或扫描仪得到的三维模型，作为仿真场景的组成部分，其数据量往往较大，若直接将其交给图形流水线处理，往往超出硬件的承受能力，无法达到实时显示的要求。

奥运主场馆区仿真场景中模型类型多，有地面、水体、植物和建筑物等类型，并且几何图形数据量较大，往往包含几万，甚至几十万个三角面。通过实验发现，即使在高配置的计算机（奔4，双CPU；2G内存）中也只有几帧每秒左右的渲染速度，没有达到实时浏览的要求。同时，为在互联网上发布奥运三维仿真场景，满足迅速获取场馆及周边地区空间信息的要求，也需要对原始模型进行一定处理，缩减文件尺寸。

自动简化技术为处理复杂、大数据量模型提供了一种解决途径。在尽量保证场景显示不失真的前提下，依据模型表面的重要程度来逐渐简化细节，从而降低硬件负担。其用途在于，能产生场景中物体的细节层次模型，来提高整个场景的渲染速度；缩减模型文件尺寸，适合网络发布和下载；自动处理技术还可以降低人工编辑大数据量三维场景的作业强度。

3.2简化技术相关工作

三角面消除算法（Schroeder, Zarge, 1992）在不损害邻近区域的局部拓扑性前提下，删除顶点和所处的三角形，同时对产生的空洞重新三角化。由于简化模型的顶点是原始模型顶点集合的子集，虽然能方便的重新利用顶点处的法向量和纹理坐标等信息，但在保真方面有所欠缺。

顶点聚类算法（Rossignac，1993）首先依据所属三角形面积或曲率为每个顶点分配一个重要度参数。然后，覆盖一个三维格网到模型上，聚类每个单元格的所有顶点到最重要的一个顶点。可见，简化的质量由三维格网的分辨率来决定。另外，在几何误差的控制上此类算法会比较困难。

迭代的边收缩算法通过不断的收缩各条边来简化模型。此类型算法的本质不同是如何选择一条边进行收缩。Hoppe在累进格网框架中的算法是依赖所有待收缩边对一个能量函数的影响程度，来将它们在优先队列中排序。二次误差度量（Garland，Heckbert，1997）算法在顶点合并操作时引入误差评价，然后依据误差大小来排序各条待收缩边。在二次型误差度量算法的基础上，引入边界约束条件和法向量限制，是本章研究的主要内容。基于边收缩不同算法的主要差异在被用于排列边的误差矩阵。这些算法一般能产生较好的显示效果，虽然运行时间有很大的不同。

3.3 二次误差度量基本原理与方法

现阶段，相当多的计算机图形应用要求使用复杂、高细节模型来给人更加真实的视觉感受。这样，在模型制作时，就要求达到非常高的分辨率来满足这种细节上的需求。然而，在应用的时候并不总是要求模型以完整的模式从始至终的表现出来，且模型越复杂，计算开销越大，有时使用一个复杂模型的简化版本就足够了。因此，自动产生这些模型的简化版本成为本章节的研究目标。

首先，介绍基于迭代的边收缩和二次型误差度量简化算法，其特点是能快速的产生多边形模型的高质量近似，是一种兼顾效率和质量的方案。并且，多边形模型不仅仅是几何要素比较复杂，而且还可能包含不同的表面属性如颜色、纹理和面法向量等数据。而这种方法的一般形式，在简化模型表面几何要素的同时，还涉及到顶点的颜色和纹理属性。

     因为每个原始模型的多边形能在预处理阶段被三角化，不失一般性，假定模型仅有三角形组成。


 

选择何种收缩方式，要依赖具体应用的要求。一般说来，最佳点替代方法产生的模型外观更加忠实于原始模型。

简单的分析上面的推导，上述算法能隐含的保留表面形状的不连续性。比如说，一个立方盒子的形状，由于面是互相垂直的，沿着边移动的点的代价就比移开点的代价低。

上面推导的基本算法仅仅考虑了模型简化时的表面几何位置要素，这是明显的缺陷。下面将介绍一个基本算法的扩展，会引入表面的颜色、贴图坐标等其它属性。

 

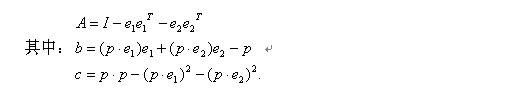
3.4 受约束二次误差度量方法

3.4.1最小值求解

     在边收缩时，采用基于二次型误差度量的方法计算两个顶点收缩到最优顶点


 

当三维模型读入，简化流程开始时，首先为每个顶点计算度量误差的矩阵，并计算每条边假若收缩，则付出的误差代价。当简化进行时，具有最小误差数值的边被收缩，此时，最优顶点作为新加入的顶点，其度量误差的矩阵为被收缩边两端点上矩阵之和。 基本算法忽略一些约束条件，现考虑将它们加入进来。

在边界曲线方面，采用的方法是，若边的三角形集合中只有小于或等于一个三角形元素时，则边被判定为边界，在误差度量时，赋予极大数值。边界的两端点在初始化阶段被认定为边界点，而边界点可能从属除边界外的其它边集合。这些边若被收缩，则会牵连到边界点的移动，从而边界有可能被改动，因而它们被判定为邻近边界的特殊集合，在误差度量时，也赋予极大数值。

在法向量偏移引起的改动方面，主要是考虑到，若一条边将被收缩，得到的最优顶点与周边顶点新组成的三角形平面，与原始三角形平面相比较，假若造成了翻转现象，则这条边的收缩应该被制止，即在误差度量时，这条边也应该被赋予极大数值。通过平面法向量点乘的计算，可得到平面间的交角，从而能预测某些边的收缩会造成翻转现象。

3.4.2约束条件算法描述

      本文实现的边折叠简化算法从折叠对象获取模型的数据开始，到中间执行边的误差度量和边折叠等操作，最后以重新计算的模型数据覆盖原始数据结束，其实现如图3.1所示。更新所有边的误差度量在算法的开始阶段进行，中间加入了约束条件，其实现如图3.2所示。更新一条边的误差度量方法在边不断的收缩过程中进行，其实现与更新所有边方法类似，不过是从折叠对象的边集合中首先删除此条边，计算度量误差后，重新插入到边集合中。
    
 

执行误差度量最小的边折叠操作，首先从折叠对象中的边集合中取出第一个元素，若其误差已经达到极大数值，则直接返回；否则，计算最佳点后，执行边折叠操作，其流程如图3.3所示。

    
    
 

3.4.3 结果分析

将三维仿真场景中的芡苓等植物模型进行原始、普通二次型度量和带约束二次型度量三种模式下成像的实验分析，可以得出如下结果。将带约束度量方法获取的三维模型图像与原始模型图像比较，通过线框模式观察，花瓣的细节被处理，但基本形状依旧保留。在实体模式下，从稍远处观察，除了茎干部分有简化后变形外，花瓣部分较难看出区别。由于三角形个数降低为原始模型三角形个数的三分之一，因而渲染速度有明显提升。
    
      
 

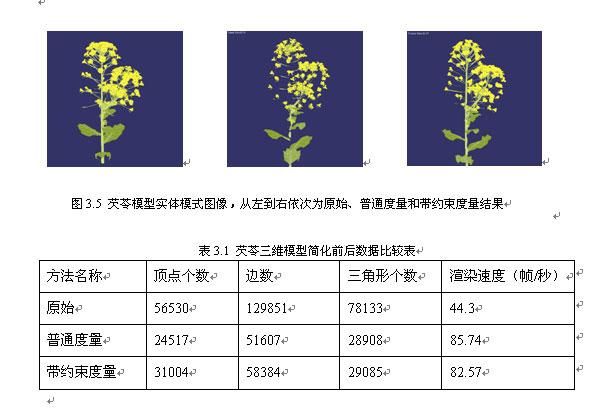
将带约束度量方法与普通度量方法相比较，在简化后得到的三角形个数相当的情况下，渲染速度基本相同（如表3.1所示），但边数与顶点个数却相差越来越大。可见两种方法选择的简化部分有所不同。从线框与实体模式的效果图（见图3.4与图3.5）均能看到，普通度量方法中的枝桠与茎干部分被简化的断断续续甚至消失，而带约束度量方法能较好的保留这些连接部分。

在简化比率（简化后三角形个数与原始个数相比）为0.5的设置下，使用带约束度量方法简化宾馆区三维仿真模型，得到的模型文件尺寸变小（如表3.2），在场景的外观上，能与原始场景保持较高的近似。经线框模式下的观察，被减掉的三角形主要集中在游泳池的水波和球场的靠背椅这些图形密集的地方（如图3.6、图3.7），而建筑物由于多为相互正交的简单平面，基本上不被简化。
    
     
       
      
        
       
         
             

3.5 本章小结

大数据量仿真场景给图形硬件造成了很大的压力，而自动简化技术为处理这类模型提供了解决途径。本章在二次误差度量算法的基础上，引入边界约束条件和法向量限制，扩展了算法的应用范围。实验结果显示，这种方法在尽量保持模型外观的前提下，处理其细节部分，达到减少了模型三角形数量，从而生成场景中不同细节层次模型的目标。也能根据在网络上发布三维场景的需求，缩减原始的模型文件尺寸到合适的大小。从三维成像效果上看，比普通二次型度量简化方法，改进算法得到的结果在外观显示上与原始模型能保持更高的相似性，有较好的显示质量。