POJ3056The Bavarian Beer Party题解动态规划DP
The Bavarian Beer Party
| Time Limit: 6000MS | Memory Limit: 65536K | |
| Total Submissions: 750 | Accepted: 253 |
Description
The professors of the Bayerische Mathematiker Verein have their annual party in the local Biergarten. They are sitting at a round table each with his own pint of beer. As a ceremony each professor raises his pint and toasts one of the other guests in such a way that no arms cross.
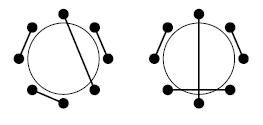
Figure 2: Toasting across a table with eight persons:no arms crossing(left), arms crossing(right)
We know that the professors like to toast with someone that is drinking the same brand of beer, and we like to maximize the number of pairs of professors toasting with the same brand , again without crossing arms. Write an algorithm to do this, keeping in mind that every professor should take part in the toasting.

Figure 2: Toasting across a table with eight persons:no arms crossing(left), arms crossing(right)
We know that the professors like to toast with someone that is drinking the same brand of beer, and we like to maximize the number of pairs of professors toasting with the same brand , again without crossing arms. Write an algorithm to do this, keeping in mind that every professor should take part in the toasting.
Input
The frist line of the input contains a single number: the number of test cases to follow. Each test case has the following format:
One line with an even number p, satisfying 2 <= p <= 1000: the number of participants
One line with p integers (separated by single spaces) indicating the beer brands fro the consecutive professors( in clockwise order, starting at an arbitrary position). Each value is between 1 and 100 (boudaries included).
One line with an even number p, satisfying 2 <= p <= 1000: the number of participants
One line with p integers (separated by single spaces) indicating the beer brands fro the consecutive professors( in clockwise order, starting at an arbitrary position). Each value is between 1 and 100 (boudaries included).
Output
For every test case in the input, the output should contain a single number on a single line: the maximum number of non-intersecting toasts of the same beer brand for this test case.
Sample Input
2 6 1 2 2 1 3 3 22 1 7 1 2 4 2 4 9 1 1 9 4 5 9 4 5 6 9 2 1 2 9
Sample Output
3 6
Source
The 2006 Benelux Algorithm Programming Contest
求最大配对数不能有交叉
状态:
d[i][j]表示第i个数到第j个数最大配对数
状态转移方程:
d[i][j]=d[i+1][j-1]+(a[i]==a[j]);
d[i][j]=max(d[i][j],d[i][k]+d[k+1][j]) (i<=k<j)
代码:
#include<cstdio> #include<cstring> #define max(a,b) ((a)>(b)?(a):(b)) int d[1005][1005],n,t,a[1005]; int main() { scanf("%d",&t); while(t--) { int i,j,k,p; memset(d,0,sizeof(d)); scanf("%d",&n); for(i=1;i<=n;i++) scanf("%d",a+i); for(p=1;p<n;p+=2) for(i=1;i+p<=n;i++) { j=i+p; d[i][j]=d[i+1][j-1]+(a[i]==a[j]); for(k=i;k<j;k++) d[i][j]=max(d[i][j],d[i][k]+d[k+1][j]); } printf("%d/n",d[1][n]); } }