如何选择样本方差的计算方法

译自：http://www.visiondummy.com/2014/03/divide-variance-n-1/

1 简介

为了回答本文的标题，在这篇文章中将介绍正太分布数据的均值和方差计算公式。如果有些读者对这些公式的背后推导不感兴趣，而仅仅只是想知道两种计算公式（除以 N 和除以 N−1 ）的使用场景，请看如下的概述

• 如果需要同时估计均值和方差（这种情况非常常见，均值和方差都未知），此时采用除以 N−1 公式，此时的方差计算公式如下：
  
  σ2=1N−1∑i=1N(xi−μ)2
• 如果样本的均值已知，只需要计算样本的方差，则此时采用除以 N−1 的公式，方差计算公式如下：
  
  σ2=1N∑i=1N(xi−μ)2
  
  前一个公式是最常用的，后一个公式经常用来估计高斯噪声的方差。因为高斯噪声的均值是已知的为0，仅仅需要估计它的方差即可。

对于正太分布的数据，可以用均值 μ 和方差 σ2 对其刻画，方差是标准差 σ 的平方，标准差表示每个样本点偏离均值的程度。换句话说标准差刻画了数据的散布程度。对于正太分布在区间[ μ−σ,μ+σ ]中的数据占全部数据的68.3%。下图表示的是 μ=10，σ2=32=9 的高斯概率密度函数

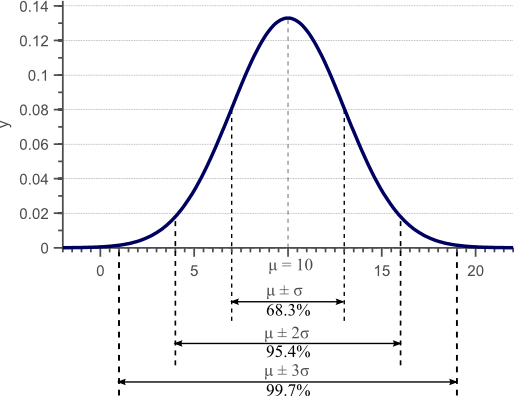
图1 高斯概率密度函数，68%的样本点落在 2σ 的区间范围内

通常情况下我们无法获得全部的样本数据。例如，在上面的例子中，我们无法获取x轴上的全部数据点，而只能获得少量的样本点，假设只能获得如下表的观察数据

表1 高斯分布的观察数据

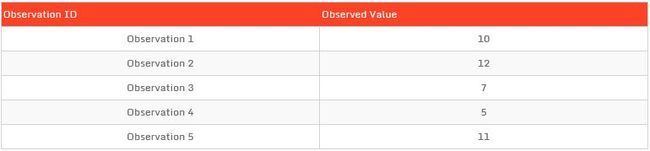
可以通过下式计算经验均值为

μ=10+12+7+5+115=9−[1]

通常加设经验均值趋近于实际均值，因此可以认为以上的观察数据来自于均值为9的高斯分布。在这个例子中 真实的样本均值为10，所以可以证明经验均值趋近于实际的样本均值。

样本的方差计算如下：

σ2=1N−1∑i=1N(xi−μ)2=(10−9)2+(12−9)2+(7−9)2+(5−9)2+(11−9)24=8.5−[2]

通常情况下假设经验方差趋近于实际方差，在这个例子中实际方差为9，这表明确实可以用经验方差代表实际方差。

现在的问题是，为什么使用如上的计算方法是正确的，如果用另一种计算方差的方法（除以 N ），如下:

σ2=1N∑i=1N(xi−μ)2=(10−9)2+(12−9)2+(7−9)2+(5−9)2+(11−9)25=6.8−[3]

[2]和[3]式的区别仅为除以的是 N−1 还是 N 。两种计算公式都是正确的，可是如何根据不同的计算情景采用不同的计算公式哪。

对参数的近似计算称为估计。下面给出一些计算符号，用 μ^ 和 σ^2 分别表示均值和方差的真值， μ 和 σ2 分别表示估计出的均值和方差的经验值。

为了获得最优的估计值，首先应该获得观测数据 xi 的似然函数，假设观测样本来自均值为 μ 和标准差为 σ 的正太分布，表示为 N(μ,σ2) ，则样本 xi 概率分布函数为:

xi∼N(μ,σ2)

⇒P(xi;μ,σ)=12πσ2−−−−√e−12σ2(xi−μ)2−4

为了估计均值和方差，至少需要两个以上的观测样本。记观测样本为 x⃗ =(x1,x2,...,xN) ，假设这些样本统计独立，可以得到观测样本的似然函数为：

P(x⃗ ;μ,σ)=P(x1,x2,...,xN;μ,σ)=P(x1;μ,σ)P(x2;μ,σ)...P(xN;μ,σ)=∏i=1NP(xi;μ,σ2)−[5]

将[4]式代入[5]中，可以得到似然函数的解析表达式

P(x⃗ ;μ,σ2)=∏i=1N12πσ2−−−−√e−12σ2(xi−μ)2=1(2πσ2)N2e−12σ2∑Ni=1(xi−μ)2−[6]

[6]式非常重要，下面将会利用这个式子到处高斯分布的均值和方差的计算公式。

2 最小方差，无偏估计

为了确定估计结果的质量，首先需要定义一个标准用于度量估计结果是否准确。估计结果的好坏与两个因素有关，即偏差(bias)和方差(variance)，下面将会讨论估计均值的方差(mean-estimator)和估计方差的方差(variance-estimator)。下面简单的讨论这两个方面。

• 参数偏差(Parameter bias)
  假设可以获得分布不重合的样本子集，与表1中的数据类似，假设还有表2，表3等不同的观测数据。则为了获得均值的最佳估计结果，需要对这些样本子集的均值做平均，平均后的均值可能会更趋近于真实的均值。虽然我们可能认为一个样本子集的经验均值不等于真实均值，一个最优的估计结果必须保证平均后的均值要等于真实均值。这种约束用数学公式表示为估计的均值等于真实的参数值，即如下
  
  E[μ]=μ^
  
  
  E[σ2]=σ^2−[7]
  
  如果估计的结果满足[7]式，则称为无偏估计。如果不满足[7] 式则称为有偏估计，此时的估计结果比真实值偏大或者偏小。
• 参数方差(Parameter variance)
  无偏估计能够保证平均后的估计结果等于真实参数。但是这并不意味着每个估计结果都是好的估计。例如，如果真实的均值为10，一个无偏估计的结果在一个样本子集上的结果为50，另一个样本子集上的估计结果为-30，估计的期望确实为10，当时估计的质量显然还依赖于每个估计的跨度。(10, 15, 5, 12, 8)和(50, -30, 100, -90, 10)的估计结果都是无偏的，都是第一个集合中的个体更接近于真实的估计值。
  因此一个好的估计不但要有低偏差，同时还要有低方差。方差可以表示为估计的均方差：
  
  Var(μ)=E[(μ^−μ)2]
  
  
  Var(σ2)=E[(σ^−σ)2]
  
  好的估计结果不但要有低偏差还要有低方差。最优的估计如果存在的话，它的偏差和方差要比任何其它的估计都要小。这种估计称为最小方差无偏估计(minimum variance, unbiased (MVU) )。下一节中将会推导高斯分布的均值和方差计算公式。将会看到在特定的假设条件下正太分布的方差MVU估计采用的是除以 N 的公式，当条件不符合时采用的是除以 N−1 的公式。

3 极大似然估计

虽然有多种技术可以估计参数，但是最简单的还是极大似然估计法。

观测数据 x⃗  的概率可以用[6]式定义为 P(x⃗ ;μ,σ2) 。固定 μ 和 σ2 ，改变 x⃗  ，可以得到如图1所示的高斯分布。如果固定 x⃗  而改变 μ 和 σ2 ，例如取 x⃗ =(10,12,7,5,11) ，同时取 μ=10 让 σ2 发生变化，图2是固定 x⃗  和 σ2 ，不同的 σ2 对应的似然函数值。

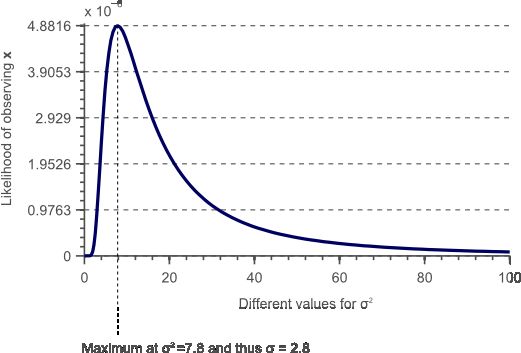
图2 固定 x⃗ ，μ=10 不同的 σ2 对应的似然函数分布
在图2中通过固定 μ=10 ，改变 σ2 计算似然函数 P(x⃗ ;σ2) ，曲线上的每个点表示从方差为 σ2 的高斯分布中采样的观测数据 x⃗  的似然函数值。曲线中的峰值对应的 σ2 最有可能是产生观测数据的分布对应的真值。因此可以把峰值对应的 σ2 当作最优的参数。在这个例子中峰值对应的 σ2=7.8 ，因此标准差为 σ2−−√=2.8 。在均值 μ=10 固定时，按照如下方法计算出的方差为7.8：

(10−10)2+(12−10)2+(7−10)2+(5−10)2+(11−10)25=7.8

因此，通过观测数据估计方差只需要找到似然函数的极大值对应的 σ 即可。如果不固定 μ ，而是 μ和σ 同时发生改变。此时要估计 μ和σ ，就需要找到二维似然函数的极大值。
为了找打函数的极大值，只要使函数的梯度为0。如果要找到二维函数的极大值，需要求解二维函数的偏导数，并使其为0。用 μ^ML 和 σ^2ML 分别表示极大似然估计方法估计的均值和方差，求解极大似然函数的偏导数，并令其为0，如下：

μ^ML=argmaxμP(x⃗ ;μ,σ2)⇒∂P(x⃗ ;μ,σ2)∂μ=0

以及

σ^2ML=argmaxσ2P(x⃗ ;μ,σ2)⇒∂P(x⃗ ;μ,σ2)∂σ2=0

稍后将会从此技术计算 μ^和σ^2 的MVU。主要考虑如下两种情况：
第一种情况为，假设 μ^ 已知，此时只要估计方差，这对应于求解一维似然函数的极大值问题，实际上这种问题在实际中并不常见，但是也有少量的实际应用。例如，如果希望计算被白噪声（也就是均值为0的高斯分布的噪声）污染的信号值，由于均值是已知的所以只需要计算方差即可。
第二种情况是，均值和方差都是未知的，这种情况是实际中最常见的。下面将介绍不同的情况下的MVU。具体来说第一种情况下使用除以 N 的方差计算公式，第二种情况使用 N−1 的方差计算公式。

4 均值已知估计方差

• 参数估计
  如果分布的均值已知，似然函数仅仅是参数 σ2 的函数，极大似然估计对应下式：
  

  σ^2ML=argmaxσ2P(x⃗ ;σ2)−[8]
  
  实际上直接计算[6]式的梯度还是比较复杂的。不过计算对数似然函数的梯度就简单的多了，因为对数函数是单调的，最大化对数似然函数和极大化原始问题是等价的，因此可以求解如下问题得到最优解：
  
  σ^2ML=argmaxσ2log(P(x⃗ ;σ2))−[9]
  
  为了表示简单，设 s=σ2 ，为了求解对数似然函数的极大值，我们计算[6]式对数的梯度并设其为0：
  
  ∂log(P(x⃗ ;σ2))∂σ2=0⇔∂log(P(x⃗ ;s))∂s=0⇔∂∂slog⎛⎝1(2πs)N2e−12s∑i=1N(xi−μ)2⎞⎠=0⇔∂∂slog⎛⎝1(2π)N2⎞⎠+∂∂slog⎛⎝⎜1(s)−−−√N2⎞⎠⎟+∂∂slog⎛⎝e−12s∑i=1N(xi−μ)2⎞⎠=0⇔∂∂slog((s)−N2)+∂∂s(−12s∑i=1N(xi−μ)2)=0⇔−N2∂∂slog(s)−12∑i=1N(xi−μ)2∂∂s(1s)=0⇔−N2s+12∑i=1N(xi−μ)2(1s2)=0⇔N2s2(−s+1N∑i=1N(xi−μ)2)=0⇔N2s2(1N∑i=1N(xi−μ)2−s)=0
  
  显然如果 N>0 ，解的结果为：
  
  s=σ2=1N∑i=1N(xi−μ)2−[10]
  
  此时极大似然估计求得的 σ^ 是计算正太分布数据的原生方法，此时的归一化因子为 1N 。
  由于极大似然估计并不能保证估计结果是无偏的。也就是说如果获得的估计是无偏的，极大似然估计法不能保证估计结果使方差最小。因此需要检测估计[10]式的估计值是否是无偏的。

• 对估计结果评估
  只要[10]式满足以下条件，其就是无偏的
  

  E[s]=s^
  
  将[10]式
  两边取平均得如下：
  
  E[s]=E[1N∑i=1N(xi−μ)2]=1N∑i=1NE[(xi−μ)2]=1N∑i=1NE[x2i−2xiμ+μ2]=1N(NE[x2i]−2NμE[xi]+Nμ2)=1N(NE[x2i]−2Nμ2+Nμ2)=1N(NE[x2i]−Nμ2)
  
  根据方差的性质 s^=E[x2i]−E[xi]2 ，因此有 E[x2i]=s^+E[xi]2=s^+μ2 ，使用以上性质看得：
  
  E[s]=1N(NE[x2i]−Nμ2)=1N(Nsˆ+Nμ2−Nμ2)=1N(Nsˆ)=sˆ
  
  即 E[s]=s^ ，因此获得的方差是无偏估计。由于极大似然法能够保证无偏估计的同时还能够保证MVU，这意味这没有其它的估计结果能比现在的结果更好。
  因此当真实的均值已知时，计算方差时需要用 N 代替 N−1 。

5 均值未知的方差估计

• 参数估计
  在上一节介绍了均值已知，估计方差的计算公式。如果均值未知，那就要同时估计均值，因为在估计方差时需要均值信息。此时上节中介绍的计算方差的方法不再是无偏的了。下面将证明，此时用 N−1 代替 N 就可以得到无偏估计了。
  和上节一样用极大似然估计方法计算均值 μ^ 的极大似然结果
  

  ∂log(P(x⃗ ;s,μ))∂μ=0⇔∂∂μlog⎛⎝1(2πs)N2e−12s∑i=1N(xi−μ)2⎞⎠=0⇔∂∂μlog⎛⎝1(2π)N2⎞⎠+∂∂μlog⎛⎝e−12s∑i=1N(xi−μ)2⎞⎠=0⇔∂∂μ(−12s∑i=1N(xi−μ)2)=0⇔−12s∂∂μ(∑i=1N(xi−μ)2)=0⇔−12s(∑i=1N−2(xi−μ))=0⇔1s(∑i=1N(xi−μ))=0⇔Ns(1N∑i=1N(xi)−μ)=0
  
  如果 N>0 以上等式的解为：
  
  μ=1N∑i=1N(xi)−[11]
  
  这就是样本均值的估计公式。现在假设[10]式的方差计算公式 s^ 仍然是MVU估计。下一节将证明在均值未知时[10]式的估计将是有偏的。

• 对估计结果评估
  只要估计结果 μ 满足[7]式，其就是无偏的
  

  E[μ]=E[1N∑i=1N(xi)]=1N∑i=1NE[xi]=1NNE[xi]=1NNμˆ
  
  因此[11]式是无偏估计，如果估计是无偏的，则极大似然估计就能保证估计的方差是最小方差估计，已经证明 μ 是均值的MVU估计。

为了检验用经验均值 μ 代替真值 μ^ 后[10]式是否依然是无偏估计，需要做如下推导：

s=σ2=1N∑i=1N(xi−μ)2=1N∑i=1N(xi−1N∑i=1N(xi))2=1N∑i=1N⎡⎣x2i−2xi1N∑i=1N(xi)+(1N∑i=1N(xi))2⎤⎦=∑i=1Nx2iN−2∑i=1Nxi∑i=1NxiN2+⎛⎝⎜⎜⎜⎜∑i=1NxiN⎞⎠⎟⎟⎟⎟2=∑i=1Nx2iN−⎛⎝⎜⎜⎜⎜∑i=1NxiN⎞⎠⎟⎟⎟⎟2

为了验证参数是否为无偏，看其是否满足[7]式：

E[s]=E⎡⎣⎢⎢⎢⎢⎢∑i=1Nx2iN−⎛⎝⎜⎜⎜⎜∑i=1NxiN⎞⎠⎟⎟⎟⎟2⎤⎦⎥⎥⎥⎥⎥=∑i=1NE[x2i]N−E⎡⎣(∑i=1Nxi)2⎤⎦N2

前面已经知道方差的计算公式有 s^=E[x2i]−E[xi]2 ，因此 E[xi]2=s^+E[x2i]=s^+μ2] ，使用以上性质可得如下等式：

E[s]=∑i=1NE[x2i]N−E⎡⎣(∑i=1Nxi)2⎤⎦N2=s+μ2−E⎡⎣(∑i=1Nxi)2⎤⎦N2=s+μ2−E[∑i=1Nx2i+∑iN∑j≠iNxixj]N2=s+μ2−E[N(s+μ2)+∑iN∑j≠iNxixj]N2=s+μ2−N(s+μ2)+∑iN∑j≠iNE[xi]E[xj]N2=s+μ2−N(s+μ2)+N(N−1)μ2N2=s+μ2−N(s+μ2)+N2μ2−Nμ2N2=s+μ2−s+μ2+Nμ2−μ2N=s+μ2−sN−μ2N−μ2+μ2N=s−sN=s(1−1N)=s(N−1N)

因为 E[s]≠s^ ，这表明方差的估计不是无偏的。随着样本数 N→∞ 偏差收敛到0。对于小样本集的情况这种偏差的影响较大，要予以消除。

• 固定偏差
  为了消除这种偏差，定义新的无偏估计 s′ 为
  
  s′=s(N−1N)−1s′=(N−1N)−11N∑i=1N(xi−μ)2s′=NN−11N∑i=1N(xi−μ)2s′=1N−1∑i=1N(xi−μ)2
  
  此时的估计 s′ 为无偏估计。注意此时的估计结果不再是最小方差估计了，但是它是最小的无偏估计。如果除以 N 则估计是有偏的，如果除以 N−1 则结果不是最小的估计方差。一般来说有偏估计的结果比稍微偏大的无偏估计结果危害更大。因此如果样本的均值是未知的应该采用除以 N−1 的公式，而不是采用除以 N 的那个公式。

6 结论

在本文中展示了正太分布的均值和方差的计算公式。证明了如果正太分布的方差已知可以采用 σ2=1N−1∑Ni=1(xi−μ)2 因子的计算公式，如果均值和方差都未知则应该用 σ2=1N∑Ni=1(xi−μ)2 。