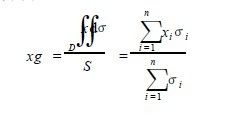计算几何-多边形的重心

1. 1　累加和求重心
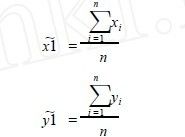
设平面上有N 个离散数据点( xi , yi ) ( i = 1, 2, ., n) , 其
多边形重心G( . x1, . y1) 为:

　　

　　这是求多边形最简单直观的方法。可以直接利用离散数
据点的x, y坐标就能求图形重心。但是缺陷在于没有对离散
数据点所围图形做任何处理和分析,精度不够。

1. 2　算法一：在讲该算法时，先要明白下面几个定理。
定理1　已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。它的重心坐标为:

　　xg = (x1+x2+x3) / 3 ;                       yg = (y1+y2+y3) / 3 ;

定理2　已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。该三角形的面积为:

　　S =  ( (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1) ) / 2 ;

　　△A1A2A3 边界构成逆时针回路时取+ , 顺时针时取 -。

　　另外在求解的过程中，不需要考虑点的输入顺序是顺时针还是逆时针，相除后就抵消了。

　　原理:将多边形划分成n个小区域, 每个小区域面积为σi ,重心为Gi ( . xi , . yi ) ,利用求平面薄板重心公式把积分变
　　成累加和:

　　　　

                           

　　　　　　　　　　　　　　　　　　

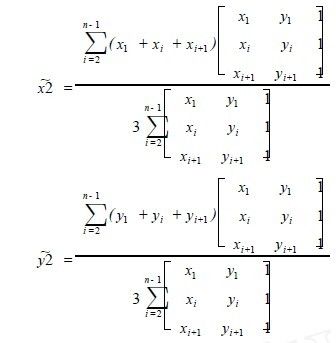
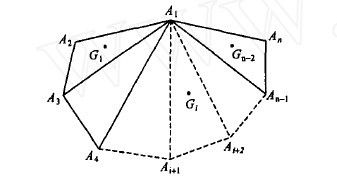
　　　　由前面所提出的原理和数学定理可以得出求离散数据点所围多边形的一般重心公式:以Ai ( xi , yi ) ( i = 1, 2, ., n) 为顶点的任意N边形A1A2 .An ,将它划　　　　分成N - 2个三角形(如图1) 。每个三角形的重心为Gi ( . xi , . yi ) ,面积为σi。那么多边形的重心坐标G( .x2, .y2) 为:

　　

                图1  多边形分解

   例题：HDU 1115 Lifting the Stone

　 代码：如下。

 

 1 #include<stdio.h>
 2 #include<math.h>
 3 #include<stdlib.h>
 4 struct centre
 5 {
 6        double x , y ;
 7 };
 8 int cas , n ;
 9 double Area( centre p0 , centre p1 , centre p2 )
10 {
11        double area = 0 ;
12        area =  p0.x * p1.y + p1.x * p2.y + p2.x * p0.y - p1.x * p0.y - p2.x * p1.y - p0.x * p2.y;
13        return area / 2 ;  // 另外在求解的过程中，不需要考虑点的输入顺序是顺时针还是逆时针，相除后就抵消了。
14 }
15 int main ()
16 {
17     centre p0 , p1 , p2 ;
18     double sum_x , sum_y , sum_area , area;
19     scanf ( "%d" , &cas ) ;
20     while ( cas -- )
21     {
22           sum_x = sum_y = sum_area = 0 ;
23           scanf ( "%d" , &n ) ;
24           scanf ( "%lf%lf" , &p0.x , &p0.y ) ;
25           scanf ( "%lf%lf" , &p1.x , &p1.y ) ;
26           for ( int i = 2 ; i < n ; ++ i )
27           {
28               scanf ( "%lf%lf" , &p2.x , &p2.y ) ;
29               area = Area(p0,p1,p2) ;
30               sum_area += area ;
31               sum_x += (p0.x + p1.x + p2.x) * area ;
32               sum_y += (p0.y + p1.y + p2.y) * area ;
33               p1 = p2 ;
34           }
35           printf ( "%.2lf %.2lf\n" , sum_x / sum_area / 3 , sum_y / sum_area / 3 ) ;
36     }
37     return 0 ;
38 }