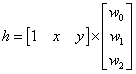Logistic回归算法简介及应用

作者：金良（[email protected]） csdn博客：http://blog.csdn.net/u012176591

情景：

二维坐标平面上有两类点集，我们知道每个点的二维直角坐标值及其类别。

需求：由一直样本的数据建立一个根据直角坐标预测类别的分类器。

logistic算法优缺点：

优点：计算代价不高，易于理解和实现

缺点：容易欠拟合，分类精度可能不高

适用数据类型：数值型和标称型数据。

利用logistic回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。

这里的回归表示找到最佳拟合的参数集合。训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法。

代码：

#encoding=UTF-8
'''
Created on 2014年6月30日

@author: jin
'''
from numpy import *
import matplotlib.pyplot as plt

def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        print lineArr
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(indata):
    return 1.0/(1+exp(-indata))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)             #转换成矩阵
    labelMat = mat(classLabels).transpose() #转换成矩阵并进行行列转置
    m,n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n,1))
    for k in range(maxCycles):              #heavy on matrix operations
        h = sigmoid(dataMatrix*weights)     #matrix mult
        error = (labelMat - h)              #vector subtraction
        weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
    return weights

def plotBestFit(weights,dataMat,labelMat):
    dataArr = array(dataMat)
    n = shape(dataArr)[0] 
    class1 = []
    class2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            class1.append([dataArr[i,1],dataArr[i,2]])
        else:
            class2.append([dataArr[i,1],dataArr[i,2]])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(list(array(class1)[:,0]), list(array(class1)[:,1]), s=30, c='red', marker='s')
    ax.scatter(list(array(class2)[:,0]), list(array(class2)[:,1]), s=30, c='green')
    x = arange(-3.0, 3.0, 0.1)
    y = array((-weights[0]-weights[1]*x)/weights[2])[0]#矩阵，1*60的，所以要第一个元素，即这60个数据
    ax.plot(x, y)
    plt.xlabel('X1')
    plt.ylabel('X2');
    plt.show()
def Main():
    dataArr,labelMat = loadDataSet()
    weights = gradAscent(array(dataArr),labelMat)#
    print weights
    plotBestFit(weights,dataArr,labelMat)
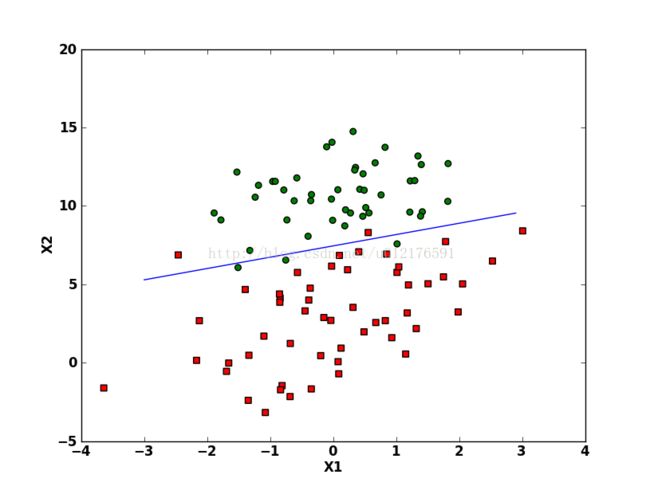
Main()

程序截图如下：

梯度上升法和梯度下降法：

梯度上升法基于的思想是：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。如果梯度记为，则函数f(x,y)的梯度由下式表示：

注意这里梯度算子只是表示移动方向，而不是移动量的大小。记该量值为，用向量来表示梯度上升算法的迭代公式如下：

该公式将一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个允许的误差范围。

梯度上升算法的示意图如下：

对自变量施加一个沿梯度算子的方向的增量，函数值越来越大。

梯度下降算法用于求函数的最小值，它与梯度上升算法是一样的，只是公式中的加法需要变成减法。因此对应的公式可以写成：

梯度下降法的示意图如下图所示，可以看到对自变量施加一个沿梯度算子相反的方向的增量，函数值变小。

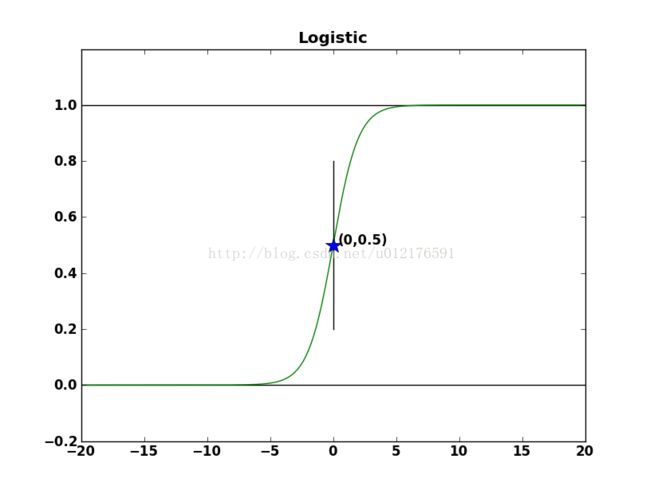
我们所使用的sigmoid函数图像如下：

可以看到函数图像的上下极限值分别是0和1，当自变量为0时，函数值为0.5，很容易发现此函数图像关于坐标点（0,0.5）呈中心对称。

作图的代码：

def sigmoid(indata):
    return 1.0/(1+exp(-indata))
x = linspace(-20,20,10000);y = sigmoid(x)
x1 = [0]*10;y1 = linspace(0.2,0.8,10);x2 = linspace(-20,20,10);y21 = [0]*10;y22 = [1]*10
plt.plot(x1,y1,'k');plt.plot(x2,y21,'k');plt.plot(x2,y22,'k');plt.plot(x,y,'g')
plt.plot([0],[0.5],'*',markersize=15)
plt.text(0.5, 0.5, '(0,0.5)')
plt.title("Logistic")
plt.ylim(-0.2,1.2) 
plt.show()

我们的样本数据的判别结果只有两个值：0和1，这恰好与sigmoid函数的上下极限相同，在训练的过程中要判别为0的数据项的判别结果会向0靠近，要判别为1的数据项的判别结果会向1靠近，其自变量分别对应负数和整数。

我们假定自变量为整数时判为1，自变量为负数时判为0。在本题中自变量的计算由输入数据项的x，y坐标值和回归系数weights计算可得：

其中x,y表示输入，即二维坐标值

我们对Main()函数做出如下修改，使其能够误判的数据项的数目：

def Main():
    dataArr,labelMat = loadDataSet()
    class1 = [];class2 = []
    for i in range(len(labelMat)):
        if labelMat[i] == 0:
            class1.append(dataArr[i])
        else:
            class2.append(dataArr[i])
    weights = gradAscent(array(dataArr),labelMat)#
    y1 = class1*weights
    y2 = class2*weights
    y1larger0 = 0
    y2smaller0 = 0
    for i in range(len(y1)):
        if y1[i] >= 0:
            y1larger0 += 1
    for i in range(len(y2)):
        if y2[i] <= 0:
            y2smaller0 += 1
    print "y1larger0:    ",y1larger0
    print "y2smaller0:    ",y2smaller0
    plotBestFit(weights,dataArr,labelMat)

控制台输出如下：

y1larger0:     0
y2smaller0:     4

也就是说，对于第一类没有错误，第二类有4个数据项发生误判

对回归系数的训练过程的运算时矩阵运算，变量h不是一个数而是一个列向量，列向量的元素个数等于样本个数，这里是100.对应的，运算dataMatrix*weights代表的不止一次乘积运算，事实上包含了300次的乘积。

下面我们对gradAscent函数进行修改，不使用矩阵运算，而是每次用一个样本对回归系数进行修正。

对最初的程序的迭代过程略作修改：

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)             #转换成矩阵
    labelMat = mat(classLabels).transpose() #转换成矩阵并进行行列转置
    m,n = shape(dataMatrix)
    alpha = 0.1
    maxCycles = 500
    weights = ones((n,1))
    for k in range(maxCycles):              #heavy on matrix operations
        #h = sigmoid(dataMatrix*weights)     #matrix mult
        #error = (labelMat - h)              #vector subtraction
        #weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
        for i in range(dataMatrix.shape[0]):
            h = sigmoid(dataMatrix[i,:]*weights)
            error = (labelMat[i]-h)
            weights = weights +alpha*dataMatrix[i,:].transpose()*error
    return weights

截图：

请注意alpha取值的放大了100倍，因为矩阵运算时是与alpha相乘的数是100个样本的误差的和，而这里与alpha相乘的数是单个样本的误差，因此只有响应地改变alpha值，才能使回归系数的学习速率保持不变。

再看对回归系数weights的学习（即修正）过程：

for k in range(maxCycles):              #heavy on matrix operations  
        h = sigmoid(dataMatrix*weights)     #matrix mult  
        error = (labelMat - h)              #vector subtraction  
        weights = weights + alpha * dataMatrix.transpose()* error #matrix mult

这次我们讨论起修正公式的推导过程：

再看画最终的分割线的程序代码：

	x = arange(-3.0, 3.0, 0.1)
    	y = array((-weights[0]-weights[1]*x)/weights[2])[0]  
    	ax.plot(x, y)

推导如下：

我们再次对函数gradAscent()进行修改：

响应的代码如下：

def gradAscent(dataMatIn, classLabels):  
    dataMatrix = mat(dataMatIn)             #转换成矩阵  
    labelMat = mat(classLabels).transpose() #转换成矩阵并进行行列转置  
    m,n = shape(dataMatrix)  
    alpha = 0.001  
    maxCycles = 5000  
    weights = ones((n,1))  
    for k in range(maxCycles):              #heavy on matrix operations  
        h = sigmoid(dataMatrix*weights)
        h1 = array(sigmoid(dataMatrix*weights))     #matrix mult
        h2 = array(labelMat-h)
        h3 = array(1-h)
        error2 = []  
        for i in range(len(h)):
            error2.append([h1[i][0]*h2[i][0]*h3[i][0]])
        error2 = mat(error2) 
        #print shape(array(h)),shape(array(h1)),shape(array(h2))
        error = (labelMat - h)              #vector subtraction  
        #print shape(error),shape(error2)
        print "error:    ",error.reshape(1,100)
        print "error2:    ",error2.reshape(1,100)
        print "\n",
        weights = weights + alpha * dataMatrix.transpose()* error2 #matrix mult  
    return weights 
 

截图：

发现效果很好