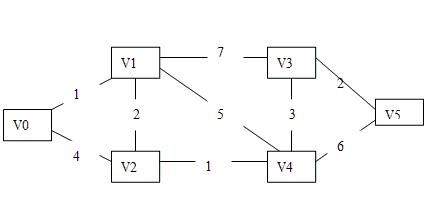
迪杰斯特拉算法处理无向图中最短路径的(dijkstra)Java实现(指定两点,求最短距离及路径)
其实不是原创哈,我写不出来。
java实现的方式如下:
第一步,根据图来建立权值矩阵:
int[][] W = {
{ 0, 1, 4, -1, -1, -1 },
{ 1, 0, 2, 7, 5, -1 },
{ 4, 2, 0, -1, 1, -1 },
{ -1, 7, -1, 0, 3, 2 },
{ -1, 5, 1, 3, 0, 6 },
{ -1, -1, -1, 2, 6, 0 } };(-1表示两边不相邻,权值无限大)
例如:W[0][2]=4 表示点V0到点V2的权值为4
W[0][3]=-1表示点V0与V3不相邻,所以权值无限大。
第二步:对V0标号;V0到其它点的路径得到 distance: {0,1,4,-1,-1,-1}; 找到V0到各点中权值最小的那个点(标号的点除外,-1代表无限大),故得到1即对应的下标1,得到V1;对V1标号,然后更改V0通过V1到其它点的路径得到 distance: { 0, 1, 3, 8, 6, -1};
第三步:找到distance中权值最小的那个点,(标号的点除外)得到V2,对V2标号,然后更改V0通过V1->V2到其它点的路径得到 distance: { 0, 1, 3, 8, 4, -1};
第四步:找到distance中权值最小的那个点,(标号的点除外)得到V4,对V4标号,然后更改V0通过V1->V2到其它点的路径得到 distance: { 0, 1, 3, 7, 4, 10};
第四步:找到distance中权值最小的那个点,(标号的点除外)得到V3,对V3标号,然后更改V0通过V1->V2到其它点的路径得到 distance: { 0, 1, 3, 7, 4, 9};
最后只剩下V5没有被标号,就找到V5了。结束!
源代码如下:
package reverse;
//这个算法用来解决无向图中任意两点的最短路径,同时输出路径(起点到所有点的)
public class Success_SQ {
public static String dijkstra(int[][] W1, int start, int end) {
System.out.println("起点:" + start + "终点:" + end);
boolean[] isLabel = new boolean[W1[0].length];// 是否标号
int[] indexs = new int[W1[0].length];// 所有标号的点的下标集合,以标号的先后顺序进行存储,实际上是一个以数组表示的栈
int i_count = -1;// 栈的顶点
int[] distance = W1[start].clone();// v0到各点的最短距离的初始值
int index = start;// 从初始点开始
int presentShortest = 0;// 当前临时最短距离
indexs[++i_count] = index;// 把已经标号的下标存入下标集中
isLabel[index] = true;
while (i_count < W1[0].length) {
// 第一步:得到与原点最近的某个点
int min = Integer.MAX_VALUE;
for (int i = 0; i < distance.length; i++) {
if (!isLabel[i] && distance[i] != -1 && i != index) {
// 如果到这个点有边,并且没有被标号
if (distance[i] < min) {
min = distance[i];
index = i;// 把下标改为当前下标
}
}
}
i_count = i_count + 1;
if(i_count == W1[0].length){
break;
}
isLabel[index] = true;// 对点进行标号
indexs[i_count] = index;// 把已经标号的下标存入下标集中
if (W1[indexs[i_count - 1]][index] == -1
|| presentShortest + W1[indexs[i_count - 1]][index] > distance[index]) {
// 如果两个点没有直接相连,或者两个点的路径大于最短路径
presentShortest = distance[index];
} else {
presentShortest += W1[indexs[i_count - 1]][index];
}
// 第二步:加入vi后,重新计算distance中的距离
for (int i = 0; i < distance.length; i++) {
// 如果vi到那个点有边,则v0到后面点的距离加
if (distance[i] == -1 && W1[index][i] != -1) {// 如果以前不可达,则现在可达了
distance[i] = presentShortest + W1[index][i];
} else if (W1[index][i] != -1 && presentShortest + W1[index][i] < distance[i]) {
// 如果以前可达,但现在的路径比以前更短,则更换成更短的路径
distance[i] = presentShortest + W1[index][i];
}
}
}
getRoute(W1,indexs,end);
return "最短距离是:" + (distance[end] - distance[start]);
}
public static void main(String[] args) {
// 建立一个权值矩阵
int[][] W1 = { // 测试数据1
{ 0, 1, 4, -1, -1, -1 },
{ 1, 0, 2, 7, 5, -1 },
{ 4, 2, 0, -1, 1, -1 },
{ -1, 7, -1, 0, 3, 2 },
{ -1, 5, 1, 3, 0, 6 },
{ -1, -1, -1, 2, 6, 0 } };
// System.out.println("f" + W1[0][4]);
int[][] W = { // 测试数据2
{ 0, 1, 3, 4 },
{ 1, 0, 2, -1 },
{ 3, 2, 0, 5 },
{ 4, -1, 5, 0 } };
System.out.println(dijkstra(W1, 5, 0)); // (int[][] W1, int start, int end)
}
// indexs:1,0,2,4,3,5 放顶点的顺序
// end:最后要的顶点名称:5
// routeLength:长度:8
/**
* seven
* 输出路径(起点到所有点的)
*/
public static String getRoute(int[][] WW, int[] indexs, int end) {
String[] routeArray = new String[indexs.length];
for (int i = 0; i < routeArray.length; i++) {
routeArray[i] = "";
}
//自己的路线
routeArray[indexs[0]] = indexs[0] + "";
for (int i = 1; i < indexs.length; i++) {
//看该点与前面所有点的连接线中的最短路径,然后得到该最短路径到底是连接了哪个点,进而此点的route就是找出那点的route+此点
int[] thePointDis = WW[indexs[i]];
int prePoint = 0;
int tmp = 9999;
for(int j=0;j<thePointDis.length;j++){
boolean chooseFlag = false;
//边的距离最短,而且,所连的点在前面的点当中
for(int m=0;m<i;m++){
if(j == indexs[m]){
chooseFlag = true;
}
}
if(chooseFlag == false){
continue;
}
if(thePointDis[j] <tmp && thePointDis[j] >0){
prePoint = j;
tmp = thePointDis[j];
}
}
routeArray[indexs[i]] = routeArray[prePoint] + indexs[i];
}
for (int i = 0; i < routeArray.length; i++) {
System.out.println(routeArray[i]);
}
return "";
}
}