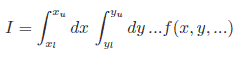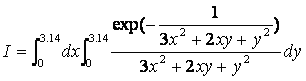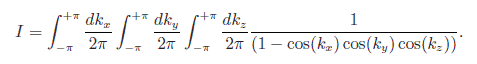GSL-蒙特卡洛积分

GSL-蒙特卡洛积分  TR:SAN E:[email protected]  2011.3.23

---------------------------------------------------------------------------

Gsl中包含有计算N重积分的蒙特卡洛方法，不过只能计算积分上下限确定的多重积分，对于上下限带有参数的积分无能为力，表达式如下：

三种蒙特卡洛积分实现方法分别定义在头文件：

#include <gsl/gsl_monte_miser.h>

#include <gsl/gsl_monte_plain.h>

#include <gsl/gsl_monte_vegas.h>

每组方法的计算思路是一样的：生成控制变量、初始化控制变量、计算积分、释放控制变量。每种方法都将用到随机数产生器。其中需要用户自定义被积分函数：

double (*f)(double * x_array, size_t dim, void * params);

其中x是积分变量数组，dim为积分变量个数，parms为额外传递的参数

对于二次函数f(x,y)=ax2+bxy+cy2，当a=3,b=2,c=1时，下面将定义目标函数：

struct my_par
{
double a,b,c;
};
double my_f( double * x_array, size_t dim, void * params )
{
my_par * mp = (my_par * ) params ;
if (dim != 2 )
{
fprintf(stderr, " dim!=2 " );
abort();
}
return x_array[ 0 ] * x_array[ 0 ] * mp -> a +
x_array[ 0 ] * x_array[ 1 ] * mp -> b +
x_array[ 1 ] * x_array[ 1 ] * mp -> c;
}

void test_monte()
{
my_par par = { 3 , 2 , 1 };
gsl_monte_function f;
f.dim = 2 ;
f.f = my_f;
f. params =& par;

}

下面介绍用法：

1. plainmonte carlo

     包含头文件：#include <gsl/gsl_monte_plain.h>

     使用步骤：

（1）       gsl_monte_plain_state* gsl_monte_plain_alloc(size_t dim);

               申请一个计算dim重积分的gsl_monte_plain_state类型控制变量

（2）       int gsl_monte_plain_init(gsl_monte_plain_state* state);

               初始化控制变量

（3）       int gsl_monte_plain_integrate (const gsl_monte_function * f,

                           const double xl[], const double xu[],

                           const size_t dim,

                           const size_t calls,

                           gsl_rng * r,

                           gsl_monte_plain_state * state,

                           double *result, double *abserr);

        计算monte carlo积分，参数意义如下：

         ：f->被积分函数

         ：xl->积分下限数组，共有dim个

         ：xu->积分上限数组，共有dim个

         ：dim->积分重数

         ：calls->目标函数被调用次数，比如500000

         ：r->随机数产生器，比如r= gsl_rng_default

         ：state->状态空间，由gsl_monte_plain_alloc申请

         ：result->计算结果

         ：abserr->绝对误差

例子：计算多重积分

#include < iostream >
#include < time.h >
#include < gsl / gsl_rng.h >
#include < gsl / gsl_integration.h >
#include < gsl / gsl_monte.h >
#include < gsl / gsl_monte_miser.h >
#include < gsl / gsl_monte_plain.h >
#include < gsl / gsl_monte_vegas.h >
using namespace std;
// [email protected] SAN NUAA 2011.3.23
struct my_par
{
double a,b,c;
};
double my_f( double * x_array, size_t dim, void * params )
{
my_par * mp = (my_par * ) params ;
if (dim != 2 )
{
fprintf(stderr, " dim!=2 " );
abort();
}
double v = x_array[ 0 ] * x_array[ 0 ] * mp -> a +
x_array[ 0 ] * x_array[ 1 ] * mp -> b +
x_array[ 1 ] * x_array[ 1 ] * mp -> c;

return exp( - 1 / v) / v;
}

void test_monte()
{
my_par par = { 3 , 2 , 1 };
gsl_monte_function f;
f.dim = 2 ;
f.f = my_f;
f. params =& par;

int calls = 500000 ;
double xl[] = { 0 , 0 },xu[] = { 3.14 , 3.14 };
double result,er;
gsl_monte_plain_state * ps = gsl_monte_plain_alloc( 2 );
const gsl_rng_type * tp = gsl_rng_minstd;
gsl_rng * pr = gsl_rng_alloc(tp);
gsl_monte_plain_init(ps);
gsl_monte_plain_integrate( & f,
xl,xu, 2 ,calls,
pr,ps, & result, & er);


cout << result << endl; // ->0.913118
cout << er << endl; // ->0.0011711
/* matlab cmd:
fun = @(x,y) exp(-1./(3.*x.*x+2.*x.*y+y.*y))./( 3.*x.*x+2.*x.*y+y.*y );
quad2d(fun,0,3.14,0,3.14)
ans=0.913889482268682
*/

}
void main()
{
test_monte();
}

2.    miser monte carlo

     包含头文件：#include <gsl/gsl_monte_ miser.h>

1. gsl_monte_miser_state* gsl_monte_miser_alloc(size_t dim);申请计算dim重积分的控制变量
2. int gsl_monte_miser_init(gsl_monte_miser_state* state);初始化积分控制变量
3. 积分函数：

        int gsl_monte_miser_integrate(gsl_monte_function * f,

                                         const double xl[], const double xh[],

                                         size_t dim, size_t calls,

                                         gsl_rng *r,

                                         gsl_monte_miser_state* state,

                                         double *result, double *abserr);

    4.void gsl_monte_miser_free(gsl_monte_miser_state* state);释放控制变量

miser carlo算法有几个参数需要设置，这些参数定义在gsl_monte_miser_state。

estimate_frac：这个参数在方差计算的递归调用过程中，指明每次函数调用次数占可用函数次数的百分比，默认值为0.1

min_calls：这个参数指明每次方差评估过程中函数调用的最小次数，如果申请函数调用次数n小于min_calls，则n=min_calls。min_calls默认值为16*dim.

min_calls_per_bisection：对分步骤中，函数调用的最小次数，默认值16* min_calls

alpha：指定两个子区域的方差如何组合，默认值为2

Dither：引入变异率，打破被积函数在积分区间的对称性。默认为0，当需要引入时，建议取值0.1

3.vegasmonte carlo

包含头文件gsl_monte_vegas.h

使用步骤：

1.）gsl_monte_vegas_state* gsl_monte_vegas_alloc(size_t dim);申请一个dim重积分的控制变量

2.）int gsl_monte_vegas_init(gsl_monte_vegas_state* state);初始化控制变量

3.）int gsl_monte_vegas_integrate(gsl_monte_function * f,

                                         double xl[], double xu[],

                                         size_t dim, size_t calls,

                                         gsl_rng * r,

                                         gsl_monte_vegas_state *state,

                                         double* result, double* abserr);

4.）void gsl_monte_vegas_free (gsl_monte_vegas_state* state);释放控制变量

下面这个例子是GSL手册上的例子：

计算积分

#include < iostream >
#include < time.h >
#include < gsl / gsl_math.h >
#include < gsl / gsl_monte_miser.h >
#include < gsl / gsl_monte_plain.h >
#include < gsl / gsl_monte_vegas.h >


using namespace std;
// e: [email protected] tr:SAN ad:NUAA t:2011
const double exact = 1.3932039296 ;
double my_f( double * k, size_t dim, void * params )
{
double A = 1.0 / ( M_PI * M_PI * M_PI );
return A / ( 1.0 - cos(k[ 0 ]) * cos(k[ 1 ]) * cos(k[ 2 ]) );
}
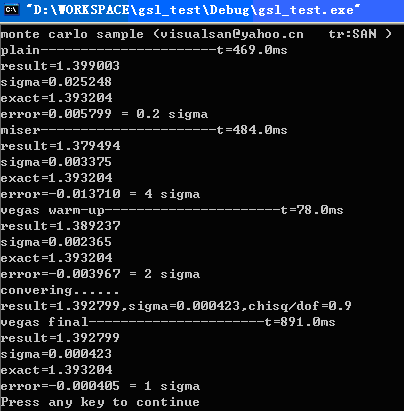
void disp_r( char * t, double r, double er, double ct)
{
printf( " %s----------------------t=%.1fms \n " ,t,ct);
printf( " result=%.6f\n " ,r);
printf( " sigma=%.6f\n " ,er);
printf( " exact=%.6f\n " ,exact);
printf( " error=%.6f = %.1g sigma\n " ,r - exact,fabs(exact - r) / er);
}
void main()
{
cout << " monte carlo sample ([email protected] tr:SAN )\n " ;
clock_t t1;
gsl_monte_function f;
f.dim = 3 ;
f.f = my_f;


int calls = 500000 ;
double xl[] = { 0 , 0 , 0 },xu[] = {M_PI,M_PI,M_PI};
double result,er;

gsl_rng_env_setup();
const gsl_rng_type * tp = gsl_rng_minstd;
gsl_rng * pr = gsl_rng_alloc(tp);



// plain
t1 = clock();
gsl_monte_plain_state * ps = gsl_monte_plain_alloc( 3 );
gsl_monte_plain_init(ps);
gsl_monte_plain_integrate( & f,
xl,xu, 3 ,calls,
pr,ps, & result, & er);
disp_r( " plain " ,result,er, ( double )(clock() - t1) );
gsl_monte_plain_free(ps);

// miser
t1 = clock();
gsl_monte_miser_state * pm = gsl_monte_miser_alloc( 3 );
gsl_monte_miser_init(pm);
gsl_monte_miser_integrate( & f,
xl,xu, 3 ,calls,
pr,pm, & result, & er);
disp_r( " miser " ,result,er,( double )(clock() - t1));
gsl_monte_miser_free(pm);

// vegas
t1 = clock();
gsl_monte_vegas_state * pv = gsl_monte_vegas_alloc( 3 );
gsl_monte_vegas_init(pv);
gsl_monte_vegas_integrate( & f,
xl,xu, 3 , 10000 ,
pr,pv, & result, & er);
disp_r( " vegas warm-up " ,result,er,( double )(clock() - t1));

printf( " convering......\n " );
t1 = clock();
do
{
gsl_monte_vegas_integrate( & f,
xl,xu, 3 ,calls / 5 ,
pr,pv, & result, & er);
printf( " result=%.6f,sigma=%.6f,chisq/dof=%.1f\n " ,result,er,pv -> chisq);
} while (fabs(pv -> chisq - 1.0 ) > 0.5 );
gsl_monte_vegas_free(pv);
disp_r( " vegas final " ,result,er,( double )(clock() - t1));

}

-------------------------------------------------------------------------------------------------

                                                                      SAN [email protected]  2011.3.23  NUAA